Download as PDF, PPTX
![O(n) - Linear Time var input = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] function linearSearch(key) { for (var i = 0; i < input.length; i++) { if (input[i] === key) return i } return null }](https://image.slidesharecdn.com/algorithms-150924060822-lva1-app6891/75/Algorithms-2-2048.jpg)
![O(log n) - Logarithmic Time var input = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] function binarySearch(key, imin, imax) { var midIndex = (imin + imax) / 2 var midNumber = input[midIndex] if (midNumber > key) { binarySearch(key, imin, midIndex - 1) } else if (midNumber < key ) { binarySearch(key, midIndex + 1, imax) } else { return midIndex } }](https://image.slidesharecdn.com/algorithms-150924060822-lva1-app6891/75/Algorithms-3-2048.jpg)
Uploaded bySantosh Rajan
Algorithms
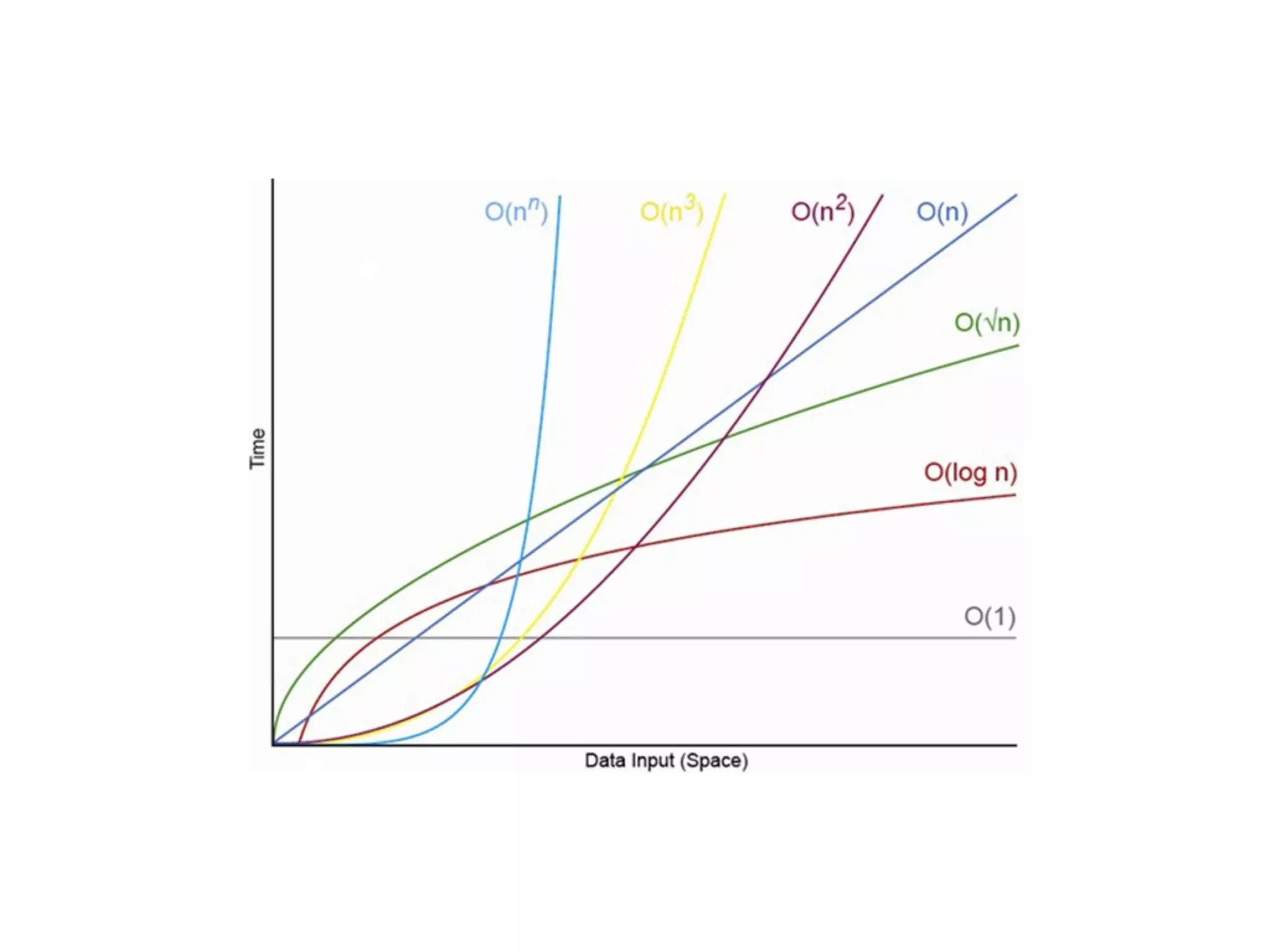
This document discusses Big O notation and time complexity of algorithms. It introduces common time complexities like O(n) linear time, O(log n) logarithmic time, and O(n^2) quadratic time. Examples are given of linear search which is O(n) and binary search which is O(log n). Common sorting algorithms are also listed like insertion sort, bubble sort, quick sort, merge sort, and selection sort along with their time complexities.
Algorithms
- 1. Big O Notation Asymptoticanalysis is the process of of describing the efficiency of algorithms as their input size (n) grows Asymptotics are usually expressed in a common format known as Big O Notation
- 2. O(n) - LinearTime var input = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] function linearSearch(key) { for (var i = 0; i < input.length; i++) { if (input[i] === key) return i } return null }
- 3. O(log n) -Logarithmic Time var input = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] function binarySearch(key, imin, imax) { var midIndex = (imin + imax) / 2 var midNumber = input[midIndex] if (midNumber > key) { binarySearch(key, imin, midIndex - 1) } else if (midNumber < key ) { binarySearch(key, midIndex + 1, imax) } else { return midIndex } }
- 4. • O(n) -Linear Time • O(log n) - Logarithmic time • O(1) - Constant time • O(n^2)
- 6. Sorting • Invariant -http://en.wikipedia.org/wiki/ Invariant_(computer_science) • Insertion Sort - http://en.wikipedia.org/wiki/Insertion_sort • Bubble Sort - http://en.wikipedia.org/wiki/Bubble_sort • Quick Sort - http://en.wikipedia.org/wiki/Quicksort • Merge Sort - http://en.wikipedia.org/wiki/Merge_sort • Selection Sort - http://en.wikipedia.org/wiki/Selection_sort