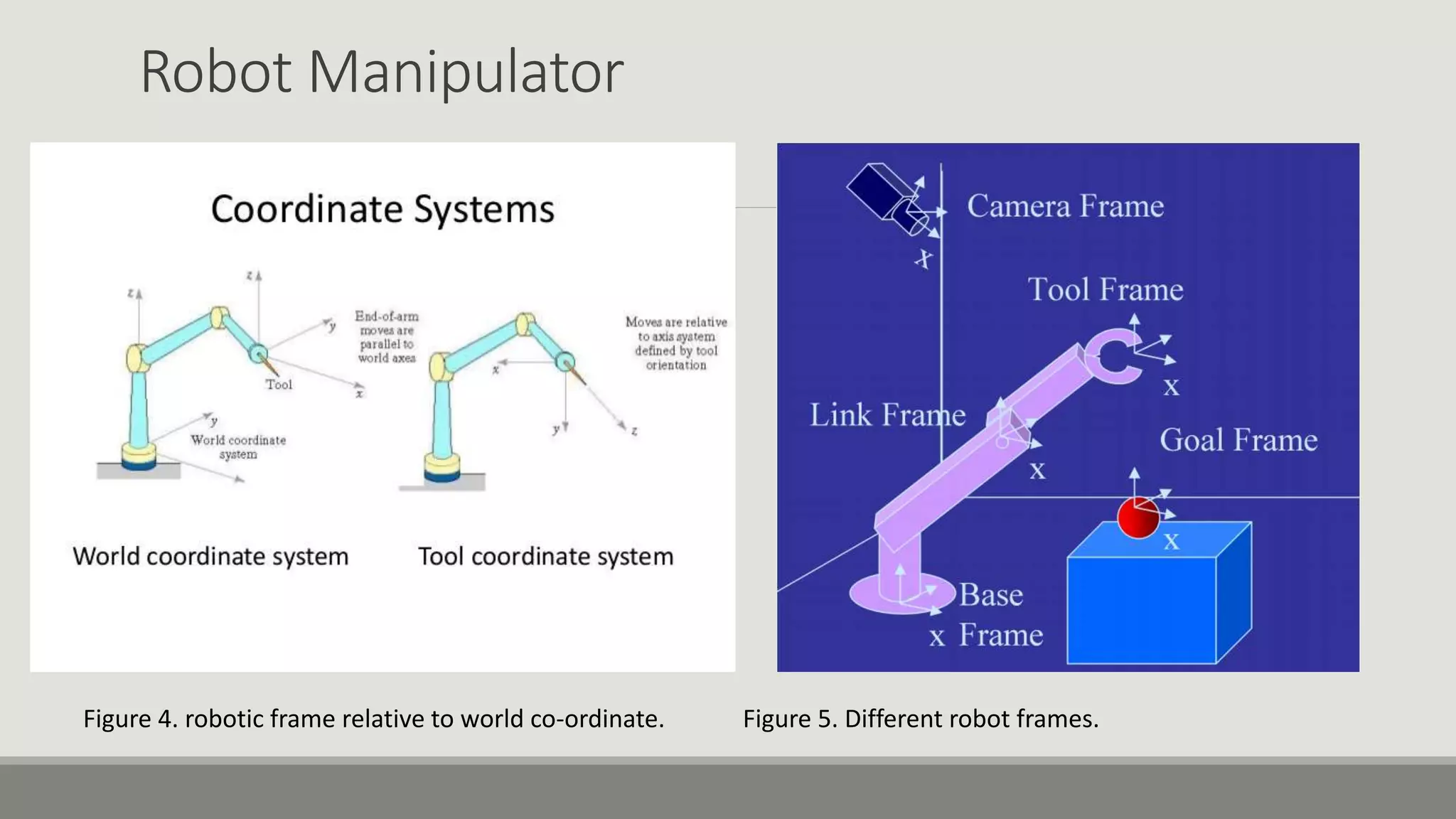
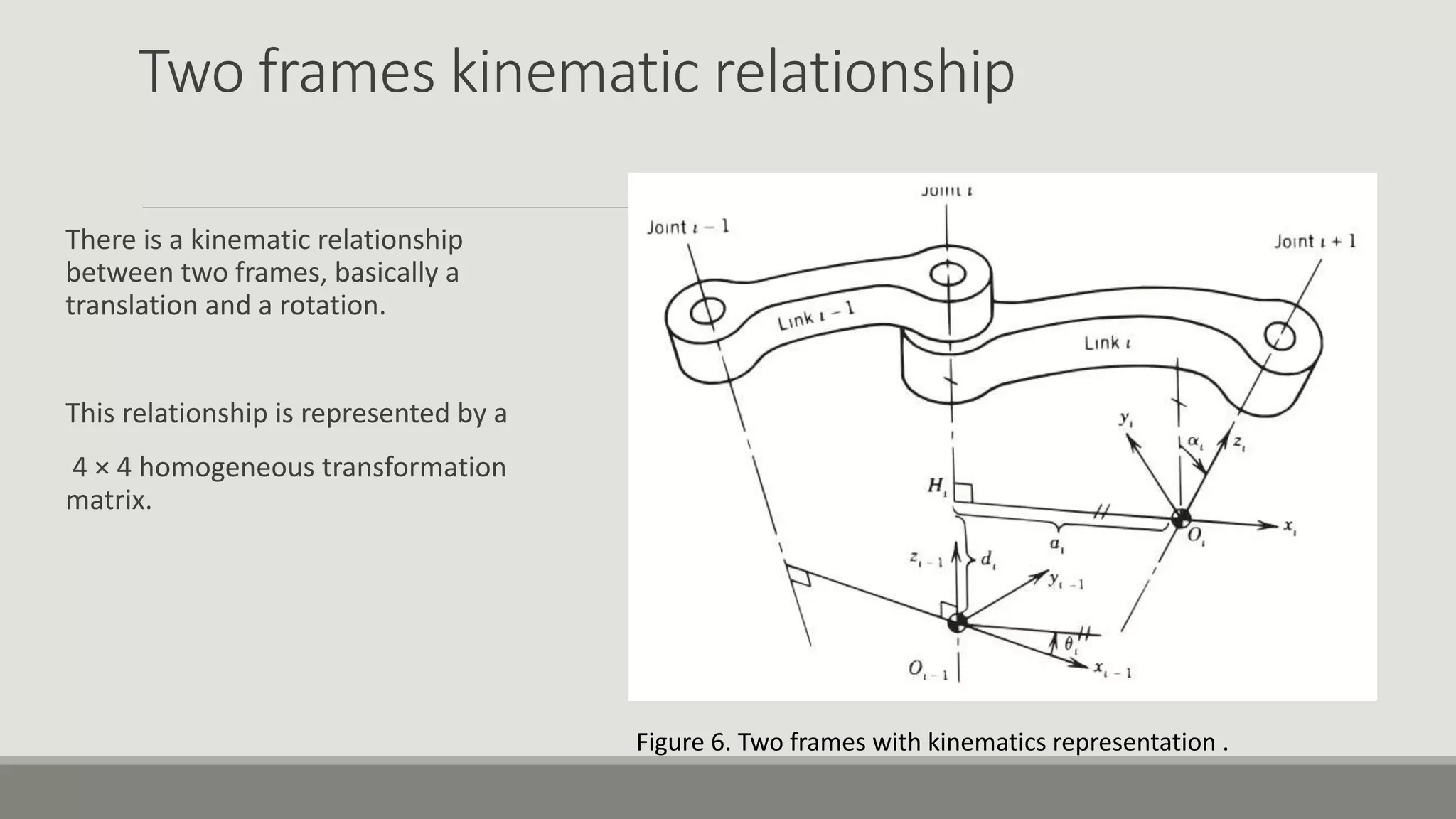
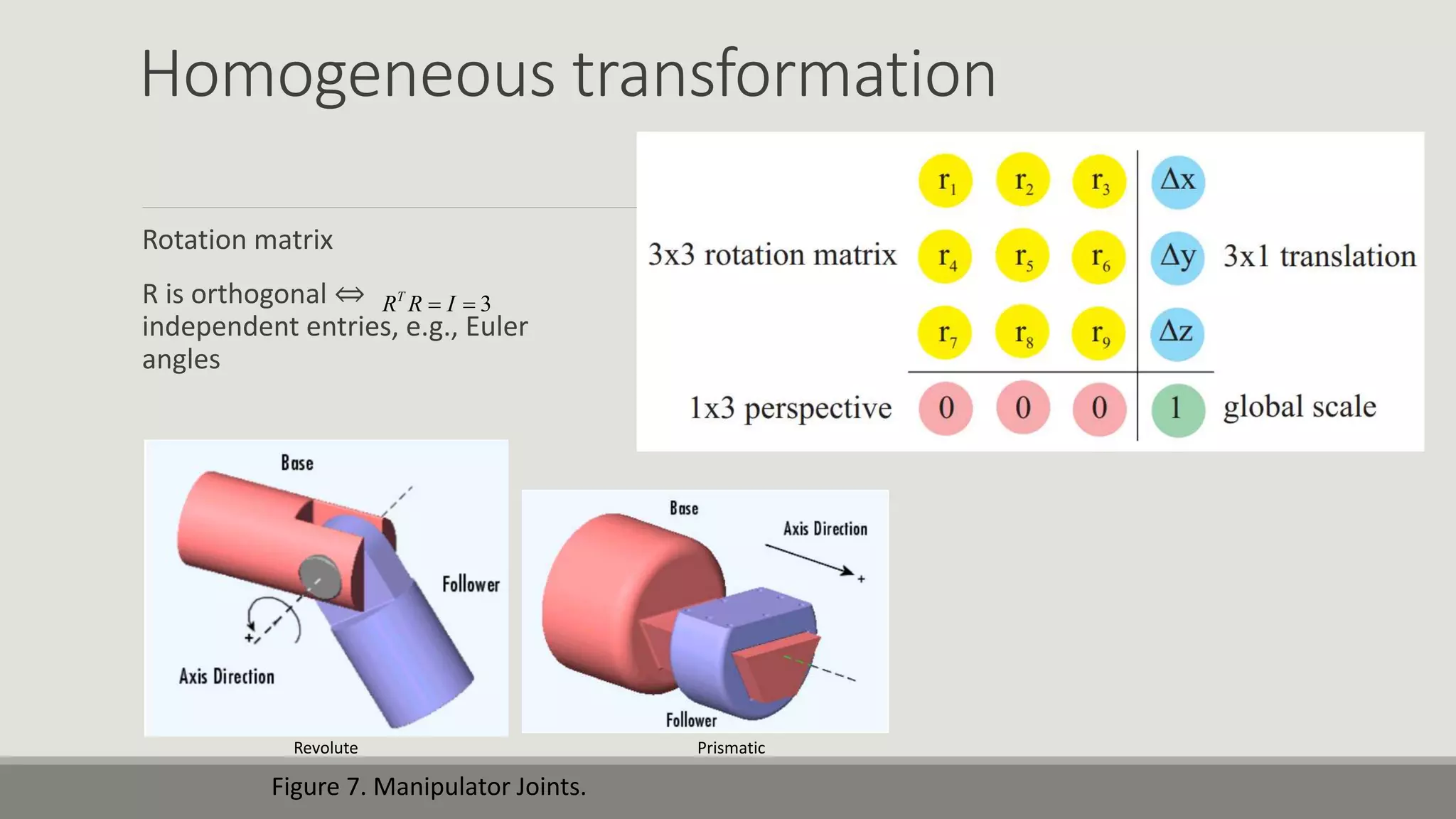
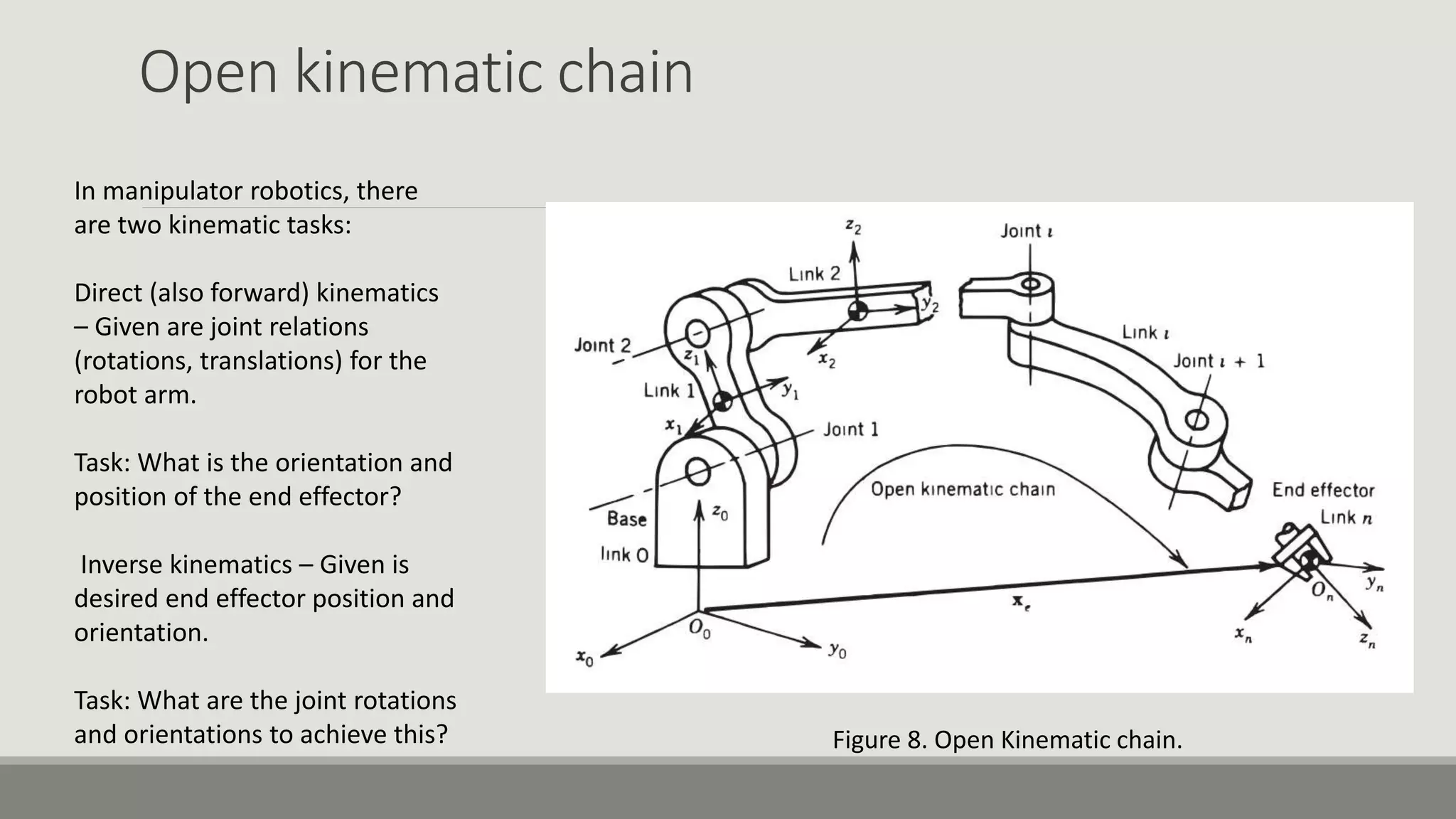
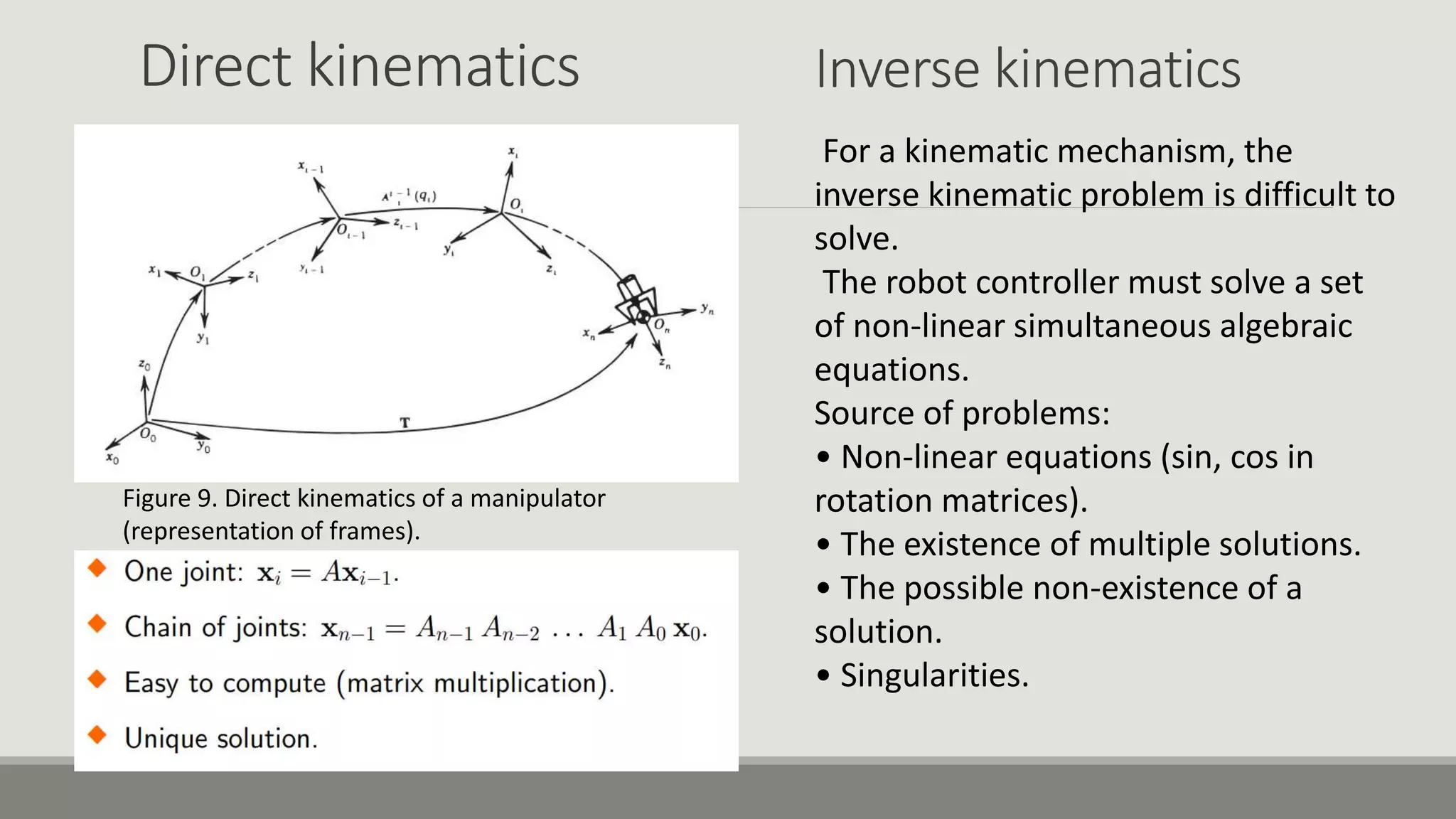
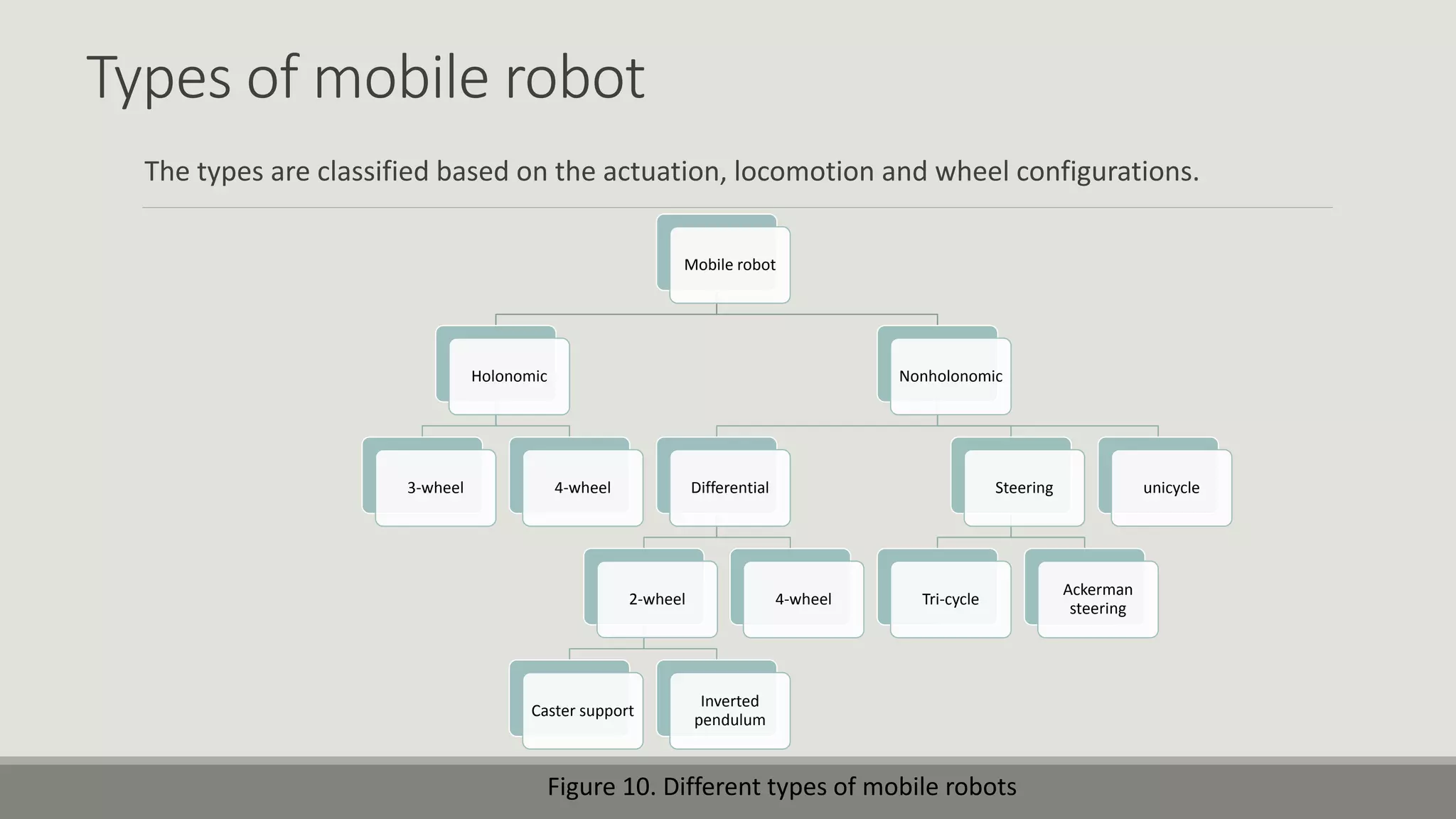
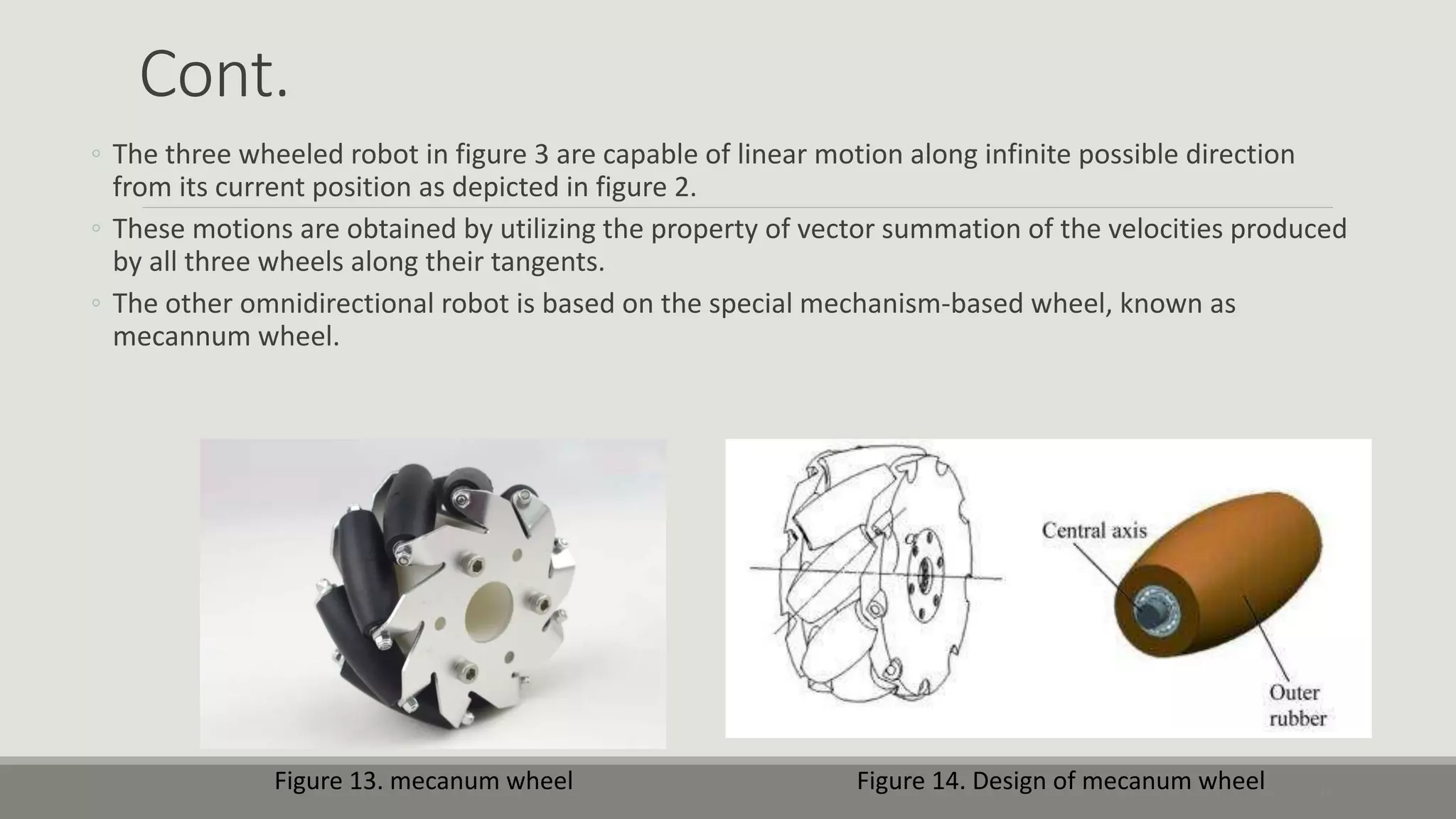
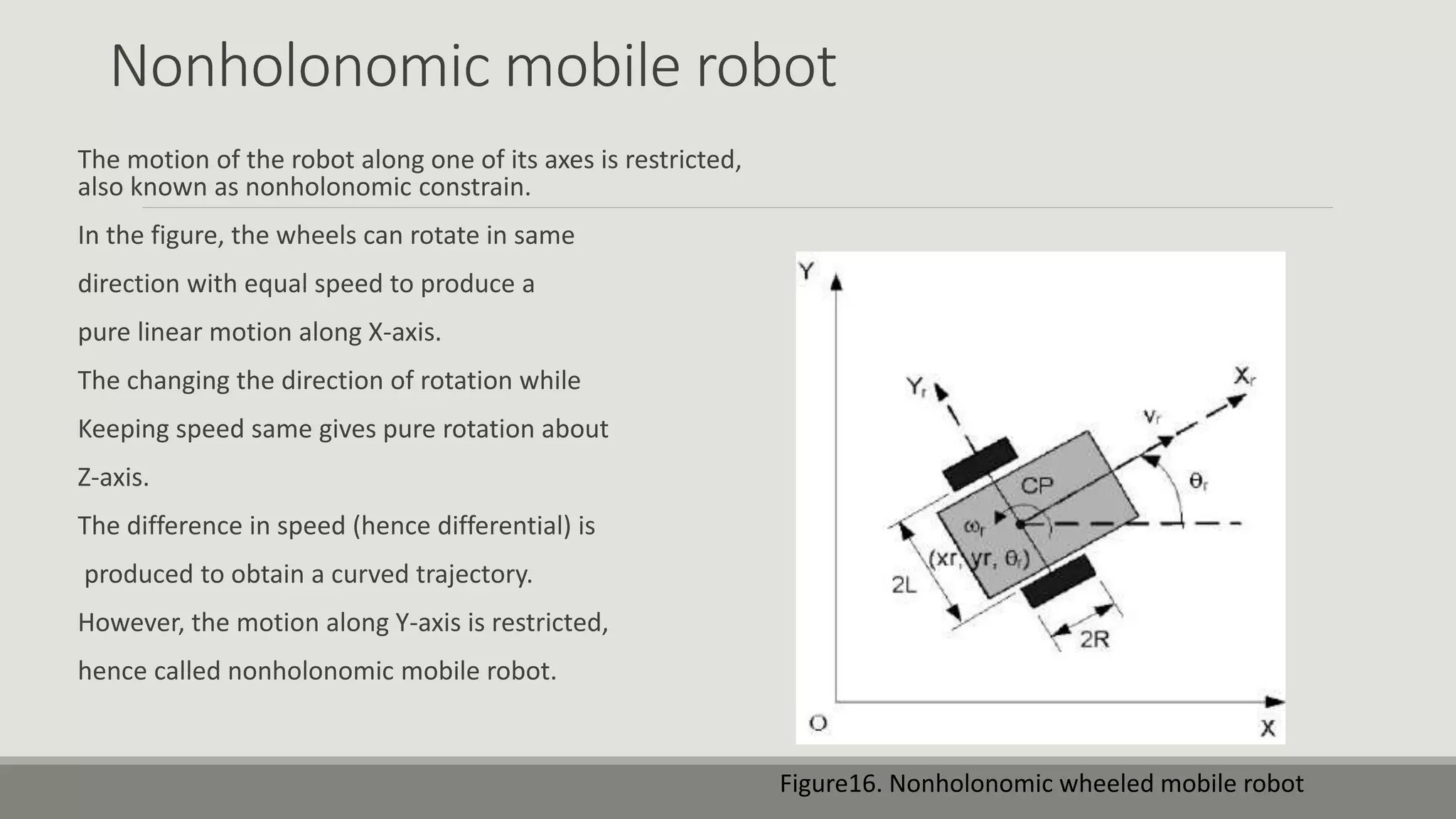
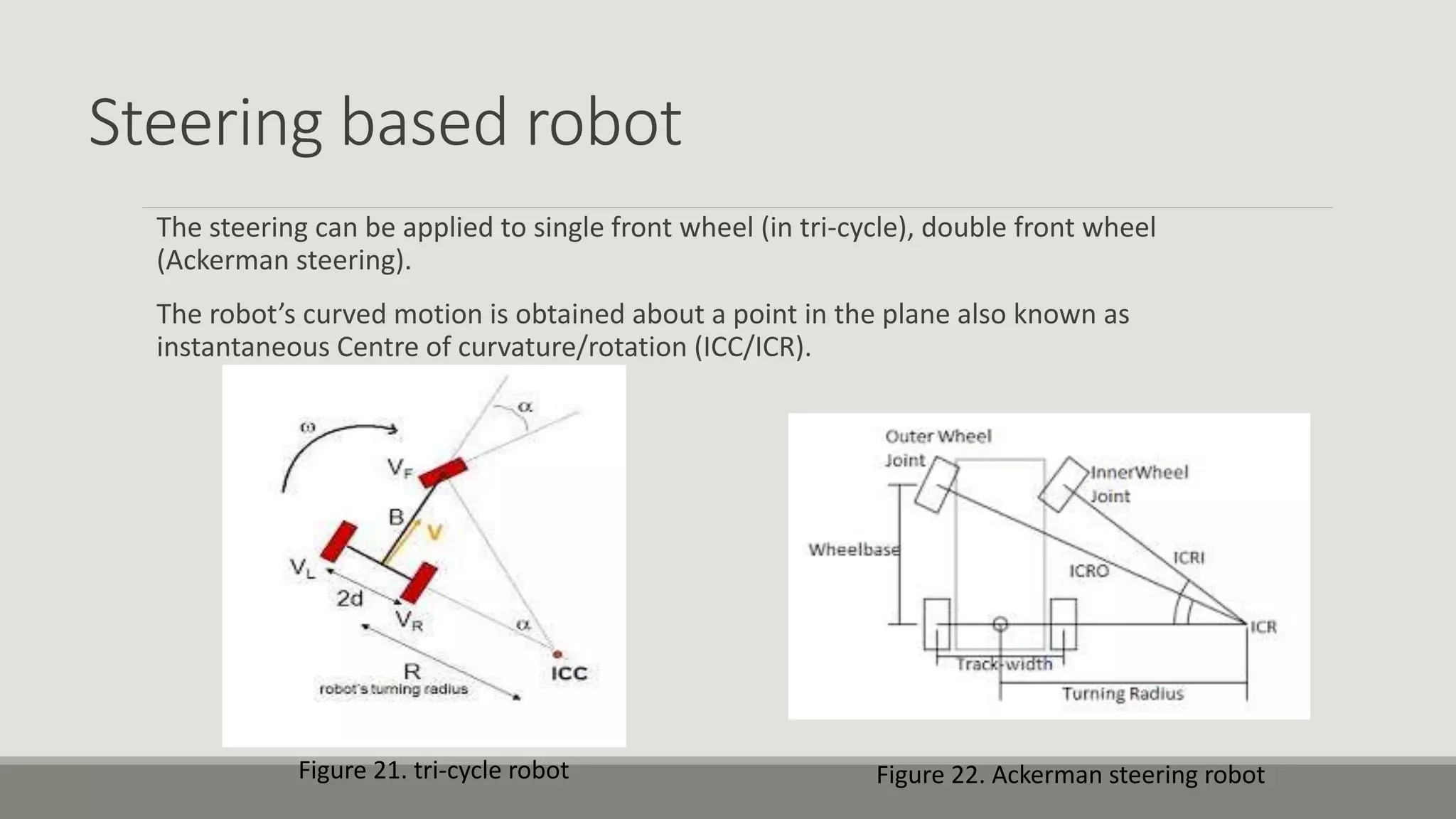
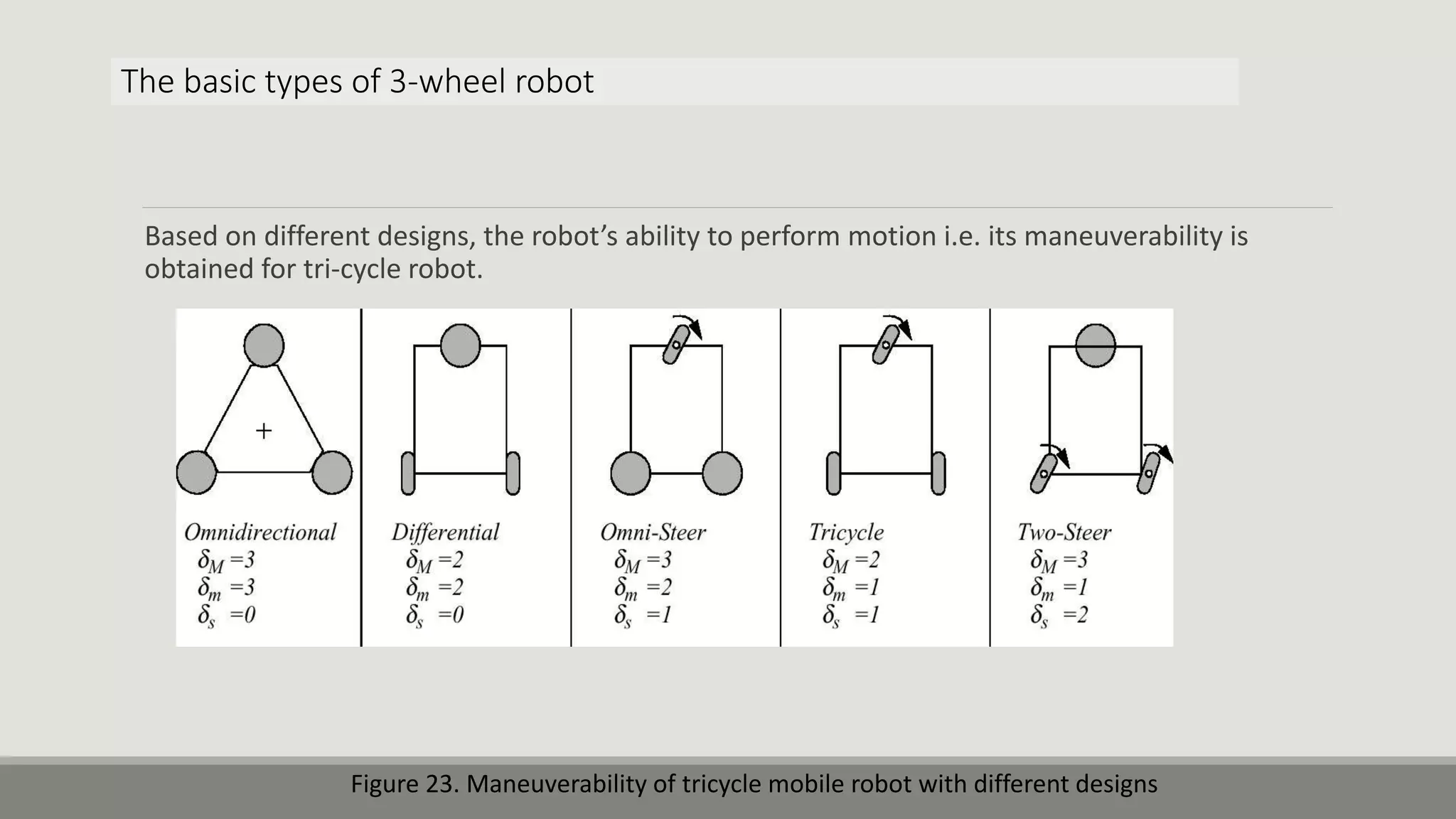
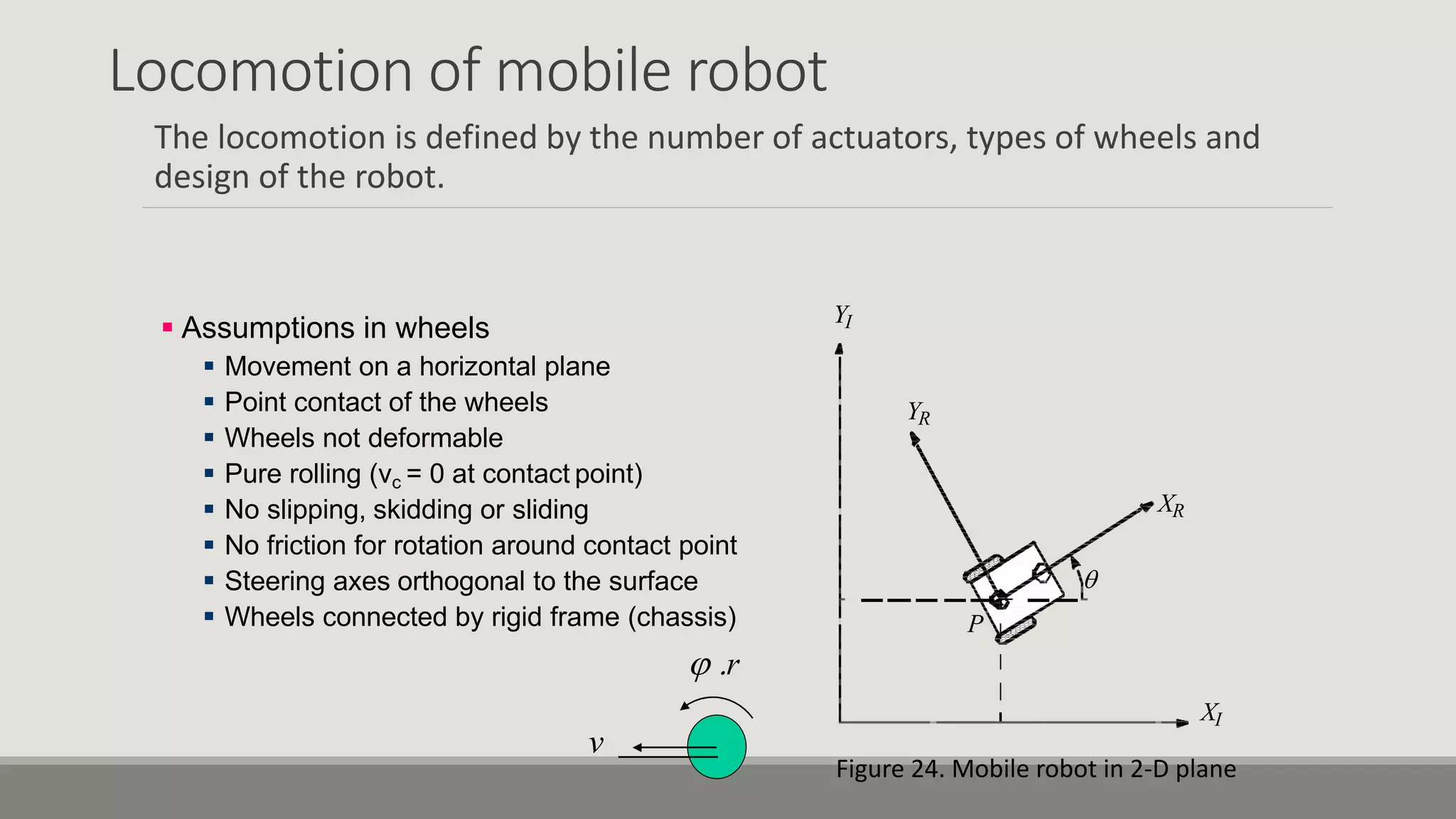
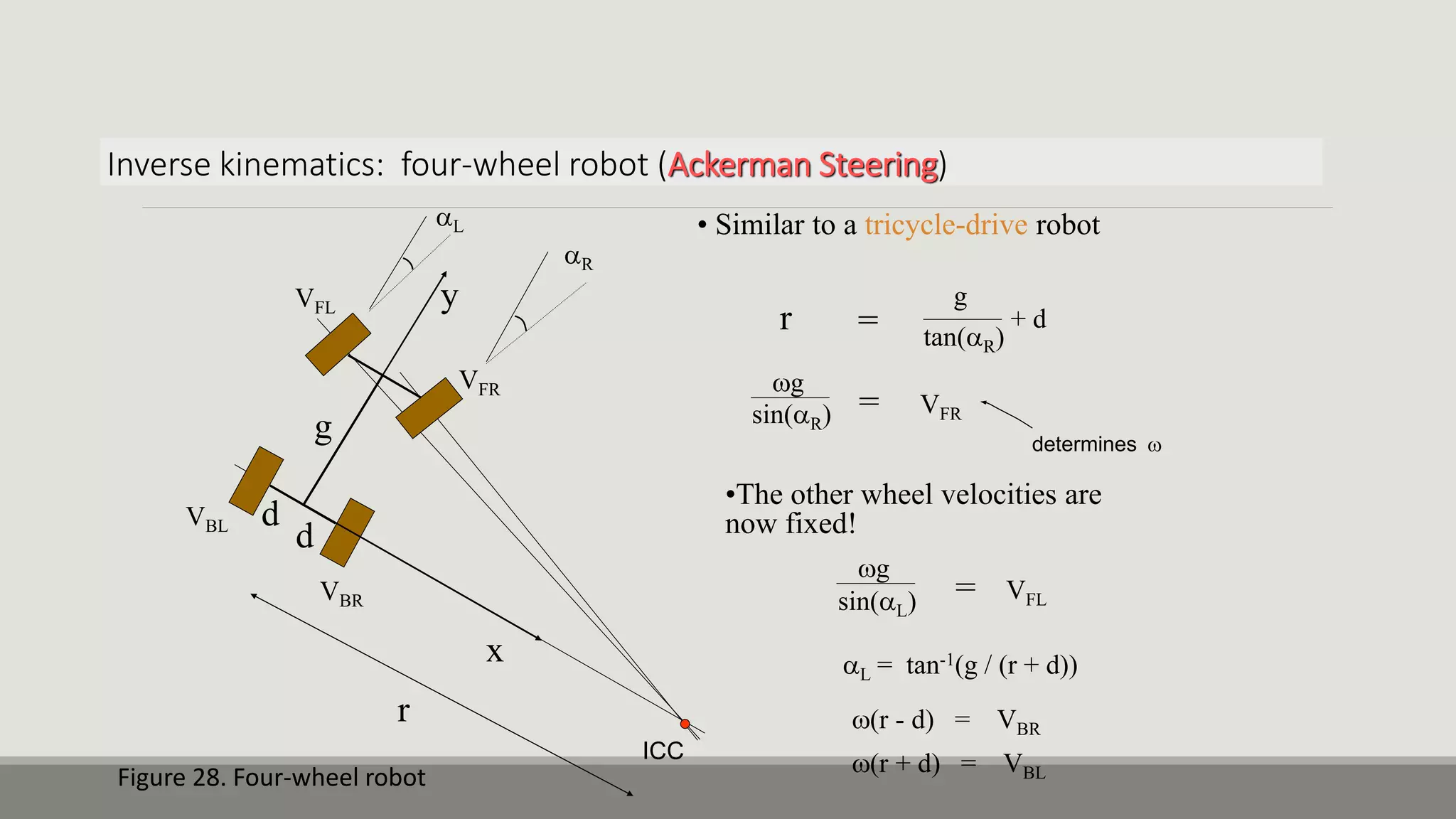
The document provides an overview of robotics, focusing on types of robots such as manipulators and mobile robots, including different locomotion mechanisms and their kinematics. It discusses direct and inverse kinematics tasks, the complexity of solving these problems, and various types of sensors and actuators used for robot control. Additionally, it outlines the fundamental concepts of mobile robot maneuverability and the necessary technology for their operation.