CLUSTBIGFIM-FREQUENT ITEMSET MINING OF BIG DATA USING PRE-PROCESSING BASED ON MAPREDUCE FRAMEWORK

CLUSTBIGFIM-FREQUENT ITEMSET MINING OF BIG DATA USING PRE-PROCESSING BASED ON MAPREDUCE FRAMEWORK

• 1.
  International Journal inFoundations of Computer Science & Technology (IJFCST), Vol.5, No.3, May 2015 DOI:10.5121/ijfcst.2015.5307 79 CLUSTBIGFIM-FREQUENT ITEMSET MINING OF BIG DATA USING PRE-PROCESSING BASED ON MAPREDUCE FRAMEWORK Sheela Gole1 and Bharat Tidke2 1 Department of Computer Engineering, Flora Institute of Technology, Pune, India ABSTRACT Now a day enormous amount of data is getting explored through Internet of Things (IoT) as technologies are advancing and people uses these technologies in day to day activities, this data is termed as Big Data having its characteristics and challenges. Frequent Itemset Mining algorithms are aimed to disclose frequent itemsets from transactional database but as the dataset size increases, it cannot be handled by traditional frequent itemset mining. MapReduce programming model solves the problem of large datasets but it has large communication cost which reduces execution efficiency. This proposed new pre-processed k-means technique applied on BigFIM algorithm. ClustBigFIM uses hybrid approach, clustering using k- means algorithm to generate Clusters from huge datasets and Apriori and Eclat to mine frequent itemsets from generated clusters using MapReduce programming model. Results shown that execution efficiency of ClustBigFIM algorithm is increased by applying k-means clustering algorithm before BigFIM algorithm as one of the pre-processing technique. KEYWORDS Association Rule Mining, Big Data, Clustering, Frequent Itemset Mining, MapReduce. 1. INTRODUCTION Data mining and KDD (Knowledge Discovery in Databases) are essential techniques to discover hidden information from large datasets with various characteristics. Now a day Big Data has bloom in various areas such as social networking, retail, web blogs, forums, online groups [1]. Frequent Itemset Mining is one of the important techniques of ARM. Goal of FIM techniques is to reveal frequent itemsets from transactional databases. Agrawal et al. [2] put forward Apriori algorithm which generates frequent itemsets having frequency greater than minimum support given. It is not efficient on single computer when dataset size increases. Enormous amount of work has been put forward to uncover frequent items. There exist various parallel and distributed algorithms which works on large datasets but having memory and I/O cost limitations and cannot handle Big Data [3] [4]. MapReduce developed by Google [5] along with hadoop distributed file system is exploited to find out frequent itemsets from Big Data on large clusters. MapReduce uses parallel computing approach and HDFS is fault tolerant system. MapReduce has Map and Reduce functions; data flow in MapReduce is shown in below figure.
• 2.
  International Journal inFoundations of Computer Science & Technology (IJFCST), Vol.5, No.3, May 2015 80 Figure 1. Map-Reduce Data flow. In this paper, based on BigFIM algorithm, a new algorithm optimizing the speed of BigFIM algorithm is proposed. Firstly using parallel K-Means clustering clusters are generated from Big Datasets. Then clusters are mined using ClustBigFIM algorithm, effectively increasing the execution efficiency. This paper is organized as follows section 2 gives overview of related work done on frequent itemset mining. Section 3 gives overview of background theory for ClustBigFIM. Section 4 explains pseudo code of ClustBigFIM. The experimental results with comparative analysis are given in section 5. Section 6 concludes the paper. 2. RELATED WORK Various sequential and parallel frequent itemset parallel algorithms are available [5] [6] [7] [8] [9] [10]. But there is need of FIM algorithms which can handle Big Data. This section gives an insight into frequent itemset mining which exploits MapReduce framework. The existing algorithms have challenges while dealing with Big Data. Parallel implementation of traditional Apriori algorithm based on MapReduce framework is put forward by Lin et al. [11] and Li et al. [12] also proposed parallel implementation of Apriori algorithm. Hammoud [13] has put forward MRApriori algorithm which is based on MapReduce programming model and classic Apriori algorithm. It does not require repetitive scan of database which uses iterative horizontal and vertical switching. Parallel implementation of FP-Growth algorithms has been put forward in [14]. Liu et al. [15] has been put forward IOMRA algorithm which is a modified FAMR algorithm optimizes execution efficiency by pre-processing using Apriori TID which removes all low frequency 1-item itemsets from given database. Then possible longest candidate itemset size is determined using length of each transaction and minimum support.
• 3.
  International Journal inFoundations of Computer Science & Technology (IJFCST), Vol.5, No.3, May 2015 81 Moens et al. [16] has been put forward two algorithms such as DistEclat and BigFIM, DistEclat is distributed version of Eclat algorithm which mines prefix tree and extracts frequent itemsets faster but not scalable enough. BigFIM applies Apriori algorithm before DistEclat to handle frequent itemsets till size k and next k+1 item are extracted using Eclat algorithm but BigFIM algorithm has limitation on speed. Both algorithms are based on MapReduce framework. Currently Moens also proposed implementations of DistEclat and BigFIM algorithms using Mahout. Approximate frequent itemsets are mined using PARMA algorithm which has been put forward by Riondato et al. [17]. K-means clustering algorithm is used for finding clusters which is called as sample list. Frequent item sets are extracted very fast, reducing execution time. Malek and Kadima [18] has been put forward parallel k-means clustering which uses MapReduce programming model for generating clusters parallel by increasing performance of traditional K- Means algorithm. It has Map, Combine and Reduce functions which uses (key, value) pair. Distance between sample point and random centres are calculated for all points using map function. Intermediate output values from map function are combined using combiner function. All samples are assigned to closest cluster using reduce function. 3. BACKGROUND 3.1. Problem Statement Let I be a set of items, I = {i1,i2,i3,…,in}, X is a set of items, X = {i1,i2,i3,…,ik} ⊆ I called k - itemset. A transaction T = {t1,t2, t3, …,tm}, denoted as T = (tid, I) where tid is transaction ID. T∈D, where D is a transactional database. The cover of itemset X in D is the set of transaction IDs containing items from X. Cover(X, D) = {tid | (tid, I) ∈D, X ⊆ I} The support of an itemset X in D is count of transactions containing items from X. Support (X, D) = |Cover(X, D)| An itemset is called frequent when its absolute minimum support threshold σ abs, with 0 ≤ σ abs ≤ |D|. Partitioning of transactions into set of groups is called clustering. Let s be the number of clusters then {C1, C2, C3… Cs} is a set of clusters from {t1,t2, t3, …,tm} , where m is number of transactions. Each transaction is assigned to only one clusters i.e. Cp ≠ φ ∧ Cp ∩ Cq for 1 ≤ p, q ≤ s, Cp is called as cluster. Let µ z be the mean of cluster Cz, squared error between mean of cluster and transactions in cluster is given as below, J (Cs ) = 2 || || s C t i s i t µ − ∑ ∈ k-means is used for minimizing sum of squared error over all S clusters and is given by, J (C ) = ∑ = S s 1 2 || || s C t i s i t µ − ∑ ∈ k-means algorithm starts with one cluster and assigns each transaction to clusters with minimum squared error.
• 4.
  International Journal inFoundations of Computer Science & Technology (IJFCST), Vol.5, No.3, May 2015 82 3.2. Apriori Algorithm Apriori is the first frequent itemset mining algorithm which has been put forward by Agarwal et al. [19]. Transactional database has transaction identifier and set of items presenting transaction. Apriori algorithm scans the horizontal database and finds frequents items of size 1-item using minimum support condition. From these frequent items discovered in iteration 1 candidate itemsets are formed and frequent itemsets of size two are extracted using minimum support condition. This process is repeated till either list of candidate itemset or frequent itemset is empty. It requires repetitive scan of database. Monotonicity property is used for removing frequent items. 3.3. Eclat Algorithm Eclat algorithm is proposed by Zaki et al. [20] which works on vertical database. TID list of each item is calculated and intersection of TID list of items is used for extracting frequent itemsets of size k+1. No need of iterative scan of database but expensive to manipulate large TID list. 3.4. k-means Algorithm The k-means algorithm [21] is well known technique of clustering which takes number of clusters as input, random points are chosen as centre of gravity and distance measures to calculate distance of each point from centre of gravity. Each point is assigned to only one cluster based on high intra-cluster similarity and low inter-cluster similarity. 4. CLUSTBIGFIM ALGORITHM This section gives high level architecture of ClustBigFIM algorithm and pseudo code of phases used in ClustBigFIM algorithm. 4.1. High Level Architecture Figure 2. High Level Architecture of ClustBigFIM Algorithm Clustering is applied on large datasets as one of the pre-processing techniques and then frequent itemsets are mined from clustered data using frequent itemset mining algorithms, Apriori and Eclat.
• 5.
  International Journal inFoundations of Computer Science & Technology (IJFCST), Vol.5, No.3, May 2015 83 4.2. ClustBigFIM on MapReduce ClustBigFIM algorithm has below phases, a. Find Clusters b. Finding k-FIs c. Generate single global TID list d. Mining of subtree 4.2.1. Find Clusters K-means clustering algorithm is used for finding clusters from given large datasets. Clusters of transactions are formed based on below formula which calculates minimum squared error, J (Cs ) = 2 || || s C t i s i t µ − ∑ ∈ and assign each transaction to the cluster. Input to this phase is transaction dataset and number of clusters, clusters of transactions are generated like C={t1,t10,...t40000}. Input : Cluster Size and Dataset Output : Clusters with size z Steps : 1. Find distance between centres and transaction id in map phase. 2. Use combiner function to combine results of above step. 3. Compute MSE using below formula and assign all points to clusters in reduce phase, J (Cs ) = 2 || || s C t i s i t µ − ∑ ∈ J (C ) = ∑ = S s 1 2 || || s C t i s i t µ − ∑ ∈ 4. Repeat steps 1-3 by changing Centre and stop when convergence criteria is reached. 4.2.2. Finding k-FIs Transaction ID list for large datasets cannot be handled by Eclat algorithm, So frequent itemsets of size k are mined from generated clusters in above phase using Apriori algorithm based on minimum support condition which handles problem of large datasets. Prefix tree is generated using frequent itemsets.
• 6.
  International Journal inFoundations of Computer Science & Technology (IJFCST), Vol.5, No.3, May 2015 84 Input : Cluster Size s, Minimum threshold σ , prefix length(l) Output : Prefixes with length l and k-FIs Steps : 5. Find support of all items in a cluster using Apriori algorithm. 6. Apply Support (xi)> σ and calculate FIs using monotonic property. 7. Repeat step 5-6 till calculating all k-FIs using mapper and reducers. 8. Repeat steps 5-7 for clusters (1 To S) and find final k-FIs. 9. Keep created prefixes in lexicographic order using lexicographic prefix tree. 4.2.3. Generate single global TID list Eclat algorithm uses vertical database, item and list of transactions where item is present. The global TID list is generated by combining local TID list using mappers and reducers. Generated TID list is used in next phase. Input : Prefix Tree, Min Supportσ Output : Single TID list of all items Steps : 10. Calculate TID list using prefix tree in map phase 11. Create single TID list from TID list generated in above step. Perform pruning with support( ia) ≤ support( ib) ↔ a < b 12. Generate prefix groups, Pk = (Pk 1 , Pk 2 , …, Pk n ) 4.2.4. Mining of Subtree Next (k+1) FIs are mined using Eclat algorithm. Prefix tree generated in phase2 is mined independently by mappers and frequent itemsets are generated. Input : Prefix tree, Minimum supportσ Output : k-FIs Steps : 13. Apply Eclat algorithm and find FIs till size k. 14. Repeat step 13 for each Subtree in map phase. 15. Find all frequent items of size k and store them in compressed trie format.
• 7.
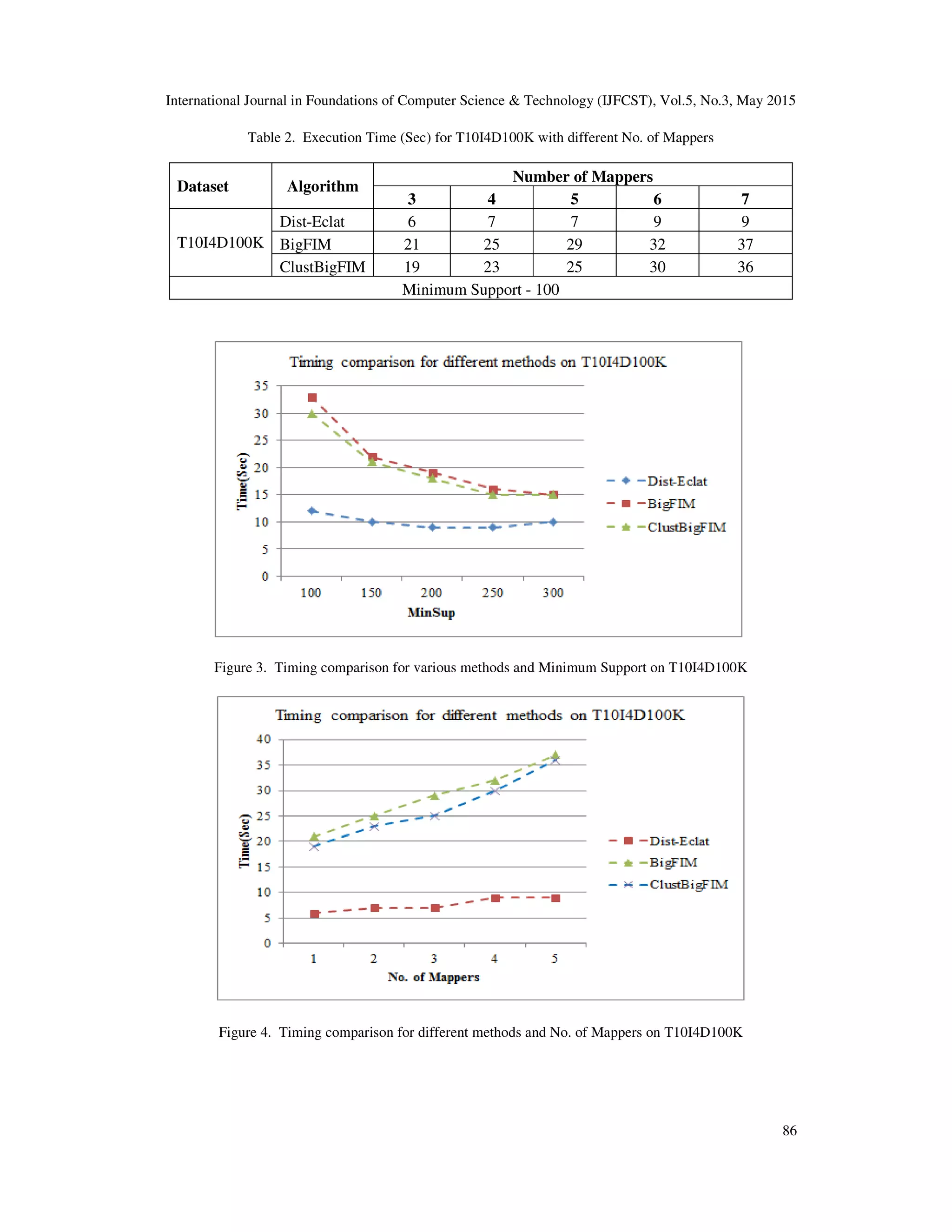
  International Journal inFoundations of Computer Science & Technology (IJFCST), Vol.5, No.3, May 2015 85 5. EXPERIMENTS This section gives overview of datasets used and experimental results with comparative analysis. For experiments 2 machines are going to be used. Each machine contains Intel® Core ™ i5- 3230M CPU@2.60GHz processing units and 6.00GB RAM with Ubuntu 12.04 and Hadoop 1.1.2. Currently algorithm run on single pseudo distributed hadoop cluster. Datasets used from standard UCI repository and FIMI repository in order to compare results with existing systems such as DistEclat and BigFIM. 5.1. Dataset Information Experiments are performed on below datasets, Mushroom – Provided by FIMI repository [22] has 119 items and 8,124 transactions. T10I4D100K- Provided by UCI repository [23] has 870 items and 100,000 transactions. Retail - Provided by UCI repository [23]. Pumsb - Provided by FIMI repository [22] has 49,046 transactions. 5.2. Results Analysis Experiments are performed on T10I4D100K, Retail, Mushroom and Pumsb dataset and execution time required for generating k-FIs is compared based on number of mappers and Minimum Support. Results shown that Dist-Eclat is faster than BigFIM and ClustBigFIM algorithm on T10I4D100K but Dist-Eclat algorithm is not working on large datasets such as Pumsb. Dist-Eclat is not scalable enough and faces memory problems as the dataset size increases. Experiments performed on T10I4D100K dataset in order to compare execution time with different Minimum Support and number of mappers on Dist-Eclat, BigFIM and ClustBigFIM. Table 1. shows Execution Time (Sec) for T10I4D100K dataset with different values of Minimum Support and 6 numbers of mappers. Figure 3. shows timing comparison for various methods on T10I4D100K dataset which shows that Dist-Eclat has faster performance over BigFIM and ClustBigFIM algorithm. Execution time decreases as Minimum Support value increases which shows effect of Minimum Support on execution time. Table 2. shows Execution Time (Sec) for T10I4D100K dataset with different values of Number of mappers and Minimum Support 100. Figure 4. shows timing comparison for various methods on T10I4D100K dataset which shows that Dist-Eclat has faster performance over BigFIM and ClustBigFIM algorithm. Execution time increases as number of mappers increases as communication cost between mappers and reducers increases. Table 1. Execution Time (Sec) for T10I4D100K with different Support. Dataset Algorithm Min. Support 100 150 200 250 300 T10I4D100K Dist-Eclat 12 10 9 9 10 BigFIM 33 22 19 16 15 ClustBigFIM 30 21 18 15 15 No. of Mappers - 6
• 8.
  International Journal inFoundations of Computer Science & Technology (IJFCST), Vol.5, No.3, May 2015 86 Table 2. Execution Time (Sec) for T10I4D100K with different No. of Mappers Dataset Algorithm Number of Mappers 3 4 5 6 7 T10I4D100K Dist-Eclat 6 7 7 9 9 BigFIM 21 25 29 32 37 ClustBigFIM 19 23 25 30 36 Minimum Support - 100 Figure 3. Timing comparison for various methods and Minimum Support on T10I4D100K Figure 4. Timing comparison for different methods and No. of Mappers on T10I4D100K
• 9.
  International Journal inFoundations of Computer Science & Technology (IJFCST), Vol.5, No.3, May 2015 87 Results have been shown that ClustBigFIM algorithm works on Big Data. Experiments are performed on Pumsb dataset. Dist-Eclat algorithm faced memory problem with Pumsb dataset. Results of ClustBigFIM are compared with BigFIM algorithm which is scalable. Table 3. and Table 4. shows execution time taken for BigFIM and ClustBigFIM algorithm on Pumsb dataset with variable Minimum Support and No. of Mappers. Number of mappers is 20 and Minimum Support is 40000 for the experiments. Figure 3. And Figure 5 and Figure 6. shows that ClustBigFIM algorithm has better performance over BigFIM algorithm due to pre- processing. Table 3. Execution Time (Sec) for Pumsb with different Support. Dataset Algorithm Min. Support 25000 30000 35000 40000 45000 Pumsb BigFIM 19462 6464 1256 453 36 ClustBigFIM 18500 5049 1100 440 30 No. of Mappers - 20 Table 4. Execution Time (Sec) for Pumsb with different No. of Mappers Dataset Algorithm Number of Mappers 10 15 20 25 30 Pumsb BigFIM 390 422 439 441 442 ClustBigFIM 385 419 435 438 438 Minimum Support - 40000 . Figure 5. Timing comparison for different methods and Minimum Support on Pumsb
• 10.
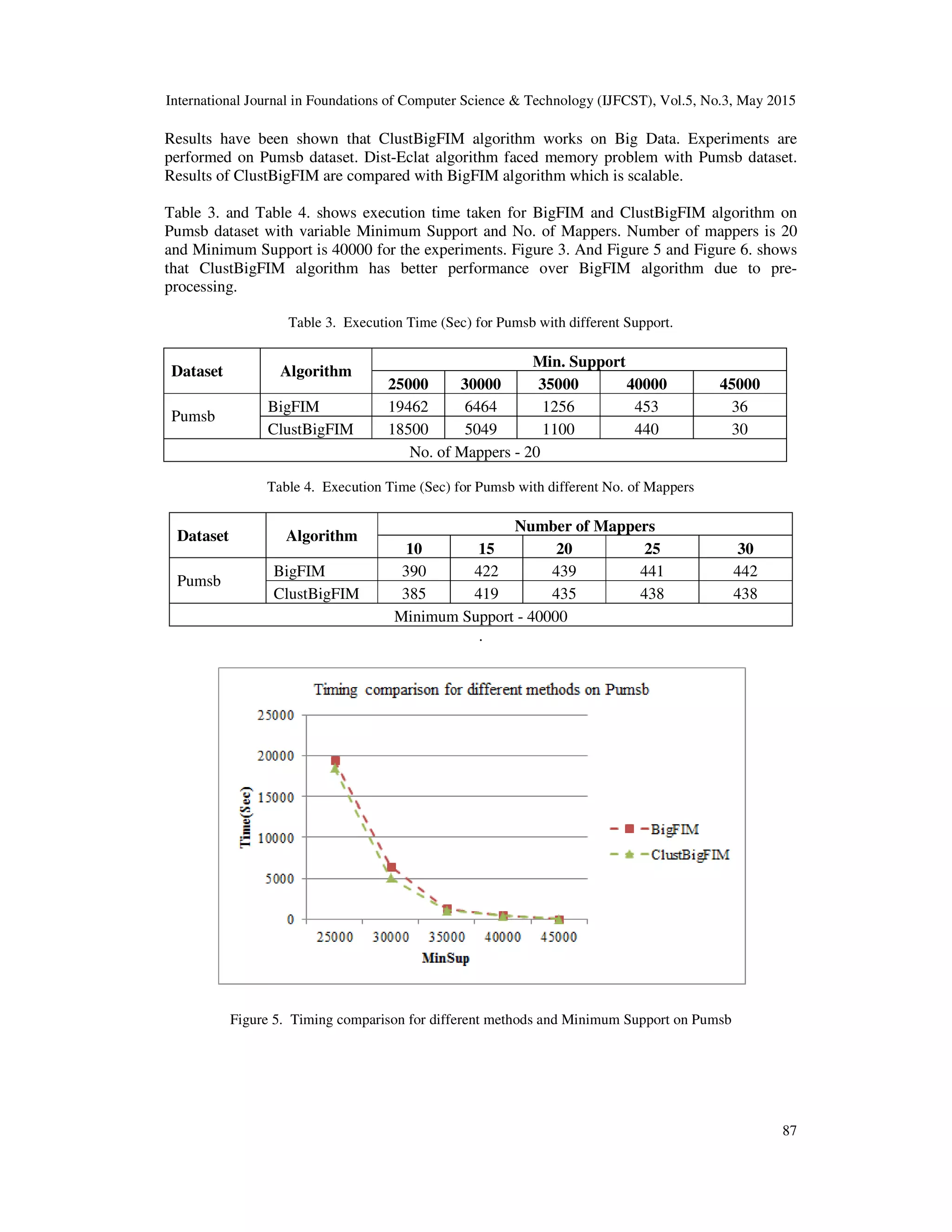
  International Journal inFoundations of Computer Science & Technology (IJFCST), Vol.5, No.3, May 2015 88 Figure 6. Timing comparison for different methods and No. of Mappers on Pumsb 6. CONCLUSIONS In this paper we implemented FIM algorithm based on MapReduce programming model. K- means clustering algorithm focuses on pre-processing, frequent itemsets of size k are mined using Apriori algorithm and discovered frequent itemsets are mined using Eclat algorithm. ClustBigFIM works on large datasets with increased execution efficiency using pre-processing. Experiments are done on transactional datasets, results shown that ClustBigFIM works on Big Data very efficiently and with higher speed. We are planning to run ClustBigFIM algorithm on different datasets for further comparative analysis. REFERENCES [1] Usama Fayyad, Gregory Piatetsky-Shapiro, and Padhraic Smyth. 1996. The KDD process for extracting useful knowledge from volumes of data. Commun. ACM 39, 11 (November 1996), 27-34. DOI=10.1145/240455.240464 [2] Rakesh Agrawal, Tomasz Imieliński, and Arun Swami. 1993. Mining association rules between sets of items in large databases. SIGMOD Rec. 22, 2 (June 1993), 207-216. DOI=10.1145/170036.170072. [3] M. Zaki, S. Parthasarathy, M. Ogihara, and W. Li. Parallel algorithms for discovery of association rules. Data Min. and Knowl. Disc., pages 343–373, 1997. [4] G. A. Andrews. Foundations of Multithreaded, Parallel, and Distributed Programming. Addison- Wesley, 2000. [5] J. Li, Y. Liu, W. k. Liao, and A. Choudhary. Parallel data mining algorithms for association rules and clustering. In Intl. Conf. on Management of Data, 2008. [6] E. Ozkural, B. Ucar, and C. Aykanat. Parallel frequent item set mining with selective item replication. IEEE Trans. Parallel Distrib. Syst., pages 1632–1640, 2011. [7] M. J. Zaki. Parallel and distributed association mining: A survey. IEEE Concurrency, pages 14–25, 1999. [8] L. Zeng, L. Li, L. Duan, K. Lu, Z. Shi, M. Wang, W. Wu, and P. Luo. Distributed data mining: a survey. Information Technology and Management, pages 403–409, 2012. [9] J. Han, J. Pei, and Y. Yin. Mining frequent patterns without candidate generation. SIGMOD Rec., pages 1–12, 2000.
• 11.
  International Journal inFoundations of Computer Science & Technology (IJFCST), Vol.5, No.3, May 2015 89 [10] L. Liu, E. Li, Y. Zhang, and Z. Tang. Optimization of frequent itemset mining on multiple-core processor. In Proceedings of the 33rd international conference on Very large data bases, VLDB ’07, pages 1275–1285. VLDB Endowment, 2007. [11] M.-Y. Lin, P.-Y. Lee and S.C. Hsueh. Apriori-based frequent itemset mining algorithms on MapReduce. In Proc. ICUIMC, pages 26–30. ACM, 2012. [12] N. Li, L. Zeng, Q. He, and Z. Shi. Parallel implementation of Apriori algorithm based on MapReduce. In Proc. SNPD, pages 236–241, 2012. [13] S. Hammoud. MapReduce Network Enabled Algorithms for Classification Based on Association Rules. Thesis, 2011. [14] L. Zhou, Z. Zhong, J. Chang, J. Li, J. Huang, and S. Feng. Balanced parallel FP-Growth with MapReduce. In Proc. YC-ICT, pages 243–246, 2010. [15] Sheng-Hui Liu; Shi-Jia Liu; Shi-Xuan Chen; Kun-Ming Yu, "IOMRA - A High Efficiency Frequent Itemset Mining Algorithm Based on the MapReduce Computation Model," Computational Science and Engineering (CSE), 2014 IEEE 17th International Conference on , vol., no., pp.1290,1295, 19-21 Dec. 2014.doi: 10.1109/CSE.2014.247 [16] Moens, S.; Aksehirli, E.; Goethals, B., "Frequent Itemset Mining for Big Data," Big Data, 2013 IEEE International Conference on , vol., no., pp.111,118, 6-9 Oct. 2013 doi: 10.1109/BigData.2013.6691742 [17] M. Riondato, J. A. DeBrabant, R. Fonseca, and E. Upfal. PARMA: a parallel randomized algorithm for approximate association rules mining in MapReduce. In Proc. CIKM, pages 85–94. ACM, 2012. [18] M. Malek and H. Kadima. Searching frequent itemsets by clustering data: towards a parallel approach using mapreduce. In Proc. WISE 2011 and 2012 Workshops, pages 251–258. Springer Berlin Heidelberg, 2013. [19] R. Agrawal and R. Srikant. Fast algorithms for mining association rules in large databases. In Proc. VLDB, pages 487–499, 1994. [20] M. Zaki, S. Parthasarathy, M. Ogihara, and W. Li. Parallel algorithms for discovery of association rules. Data Min. and Knowl. Disc., pages 343–373, 1997. [21] A K Jain, M N Murty, P. J. Flynn, ‘Data Clustering: A Review’, ACM COMPUTING SURVEYS, 1999. [22] Frequent itemset mining dataset repository. http://fimi.ua.ac.be/data, 2004. [23] T. De Bie. An information theoretic framework for data mining. In Proc. ACM SIGKDD, pages 564– 572, 2011.