Download to read offline
Contest_algorithm in VLSI testing .pptx
- 1.
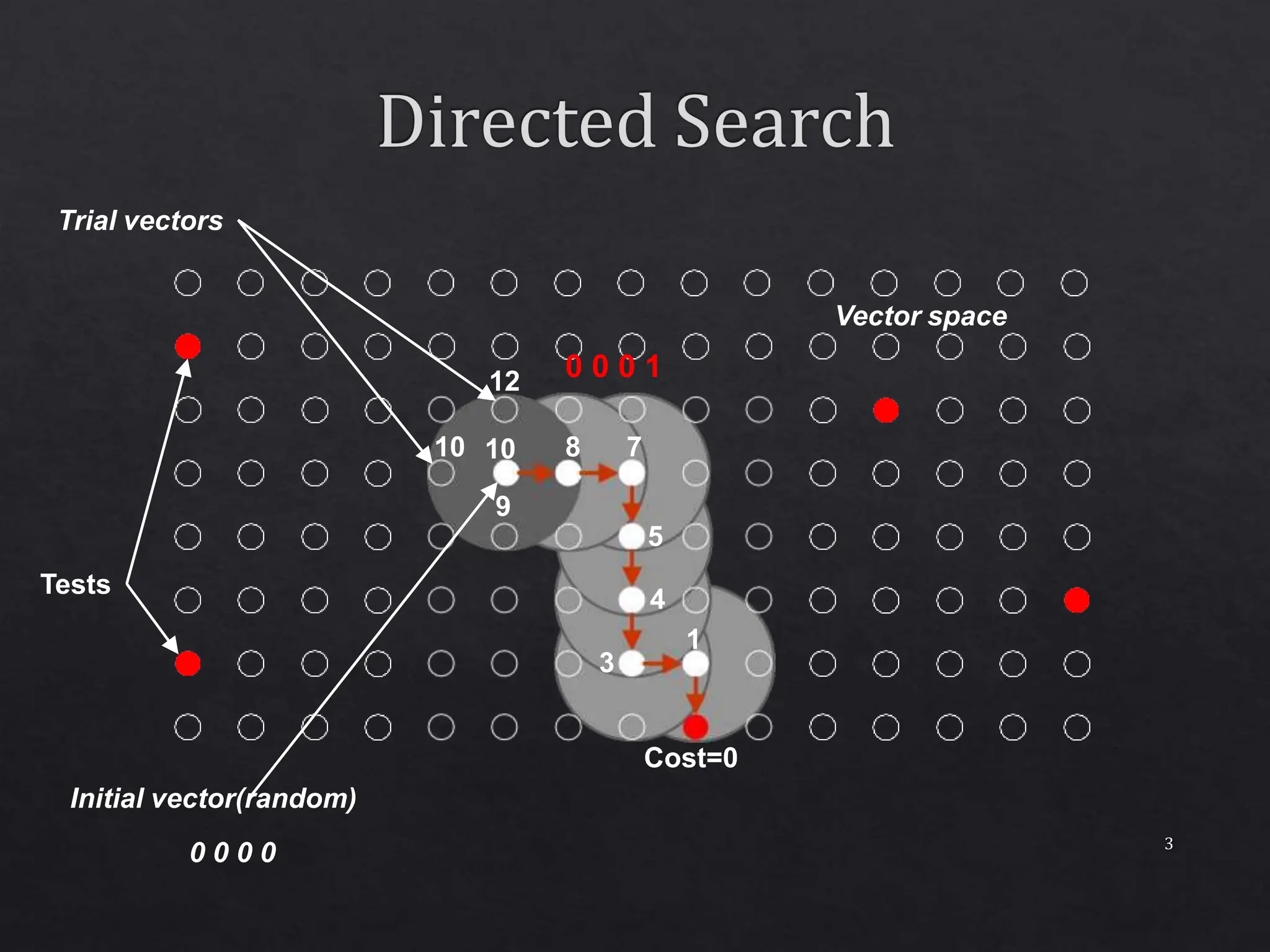
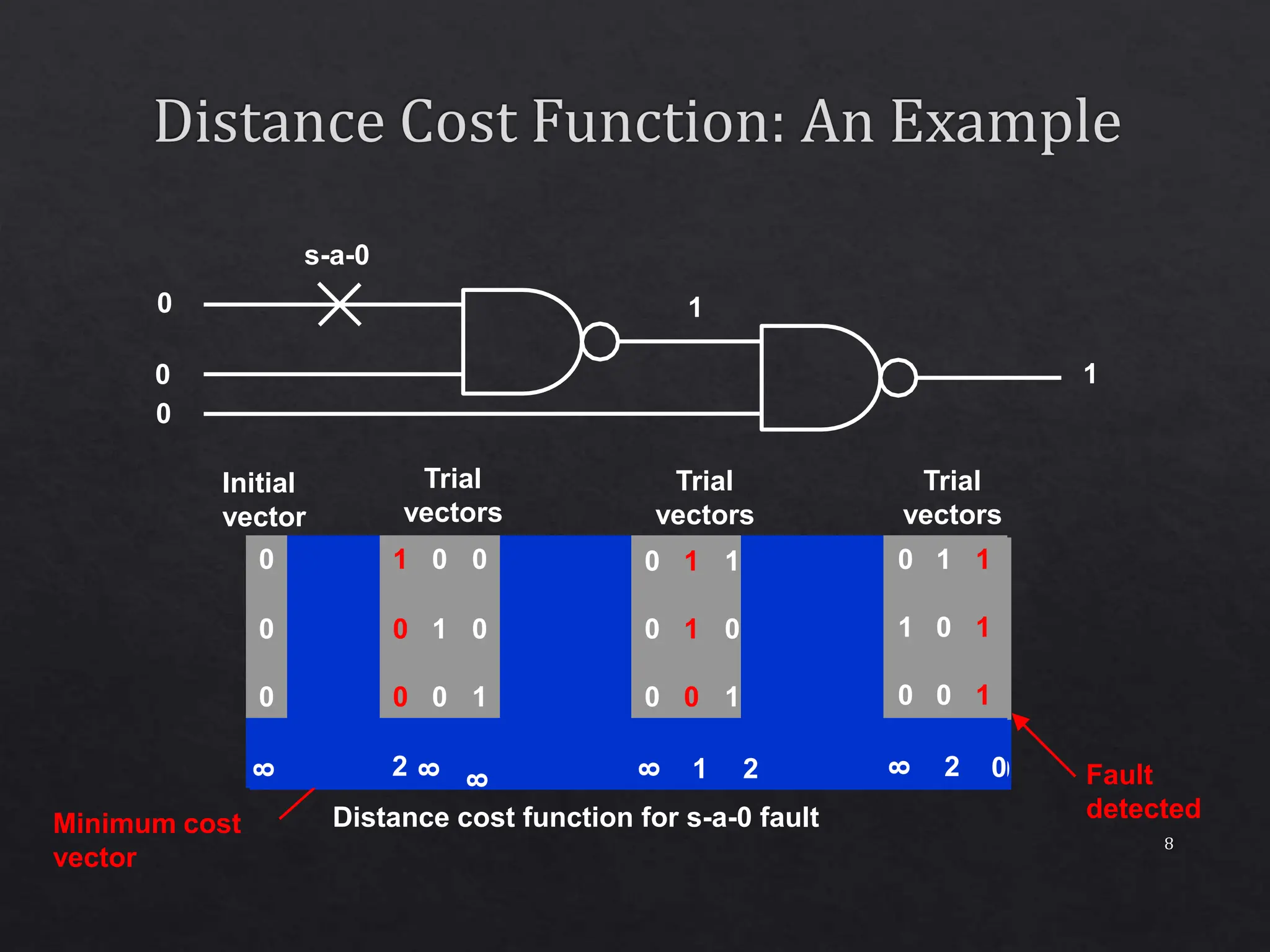
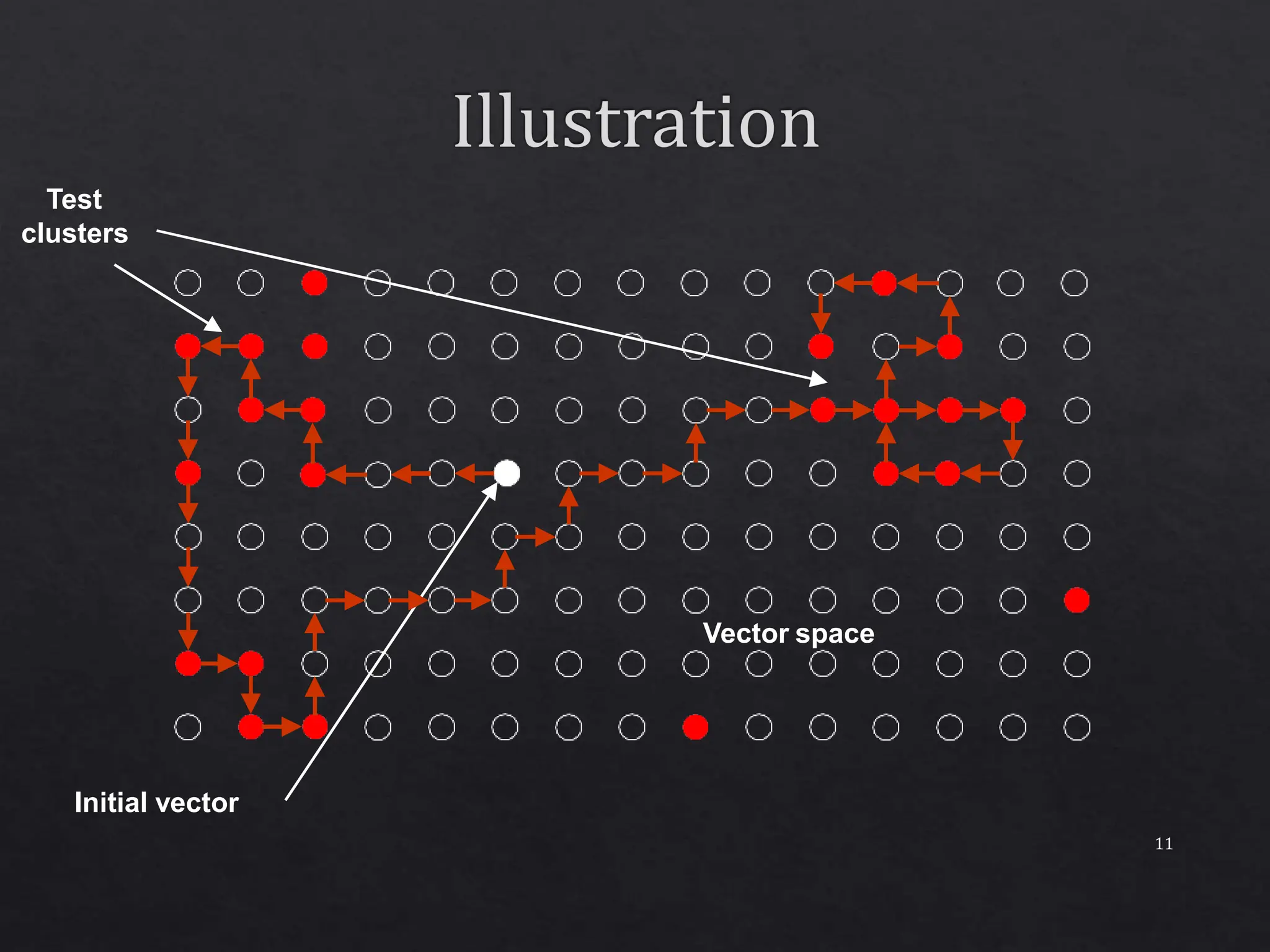
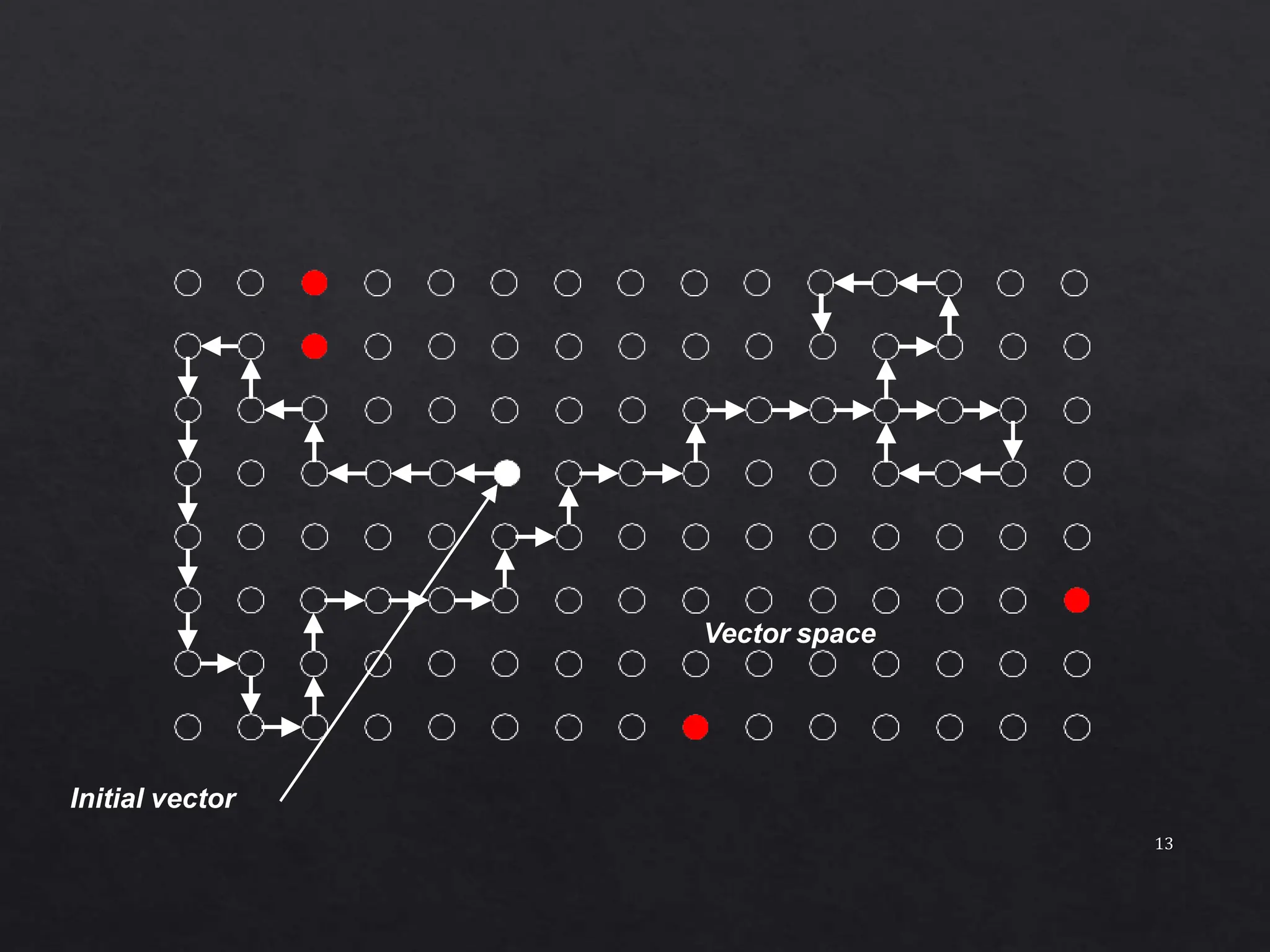
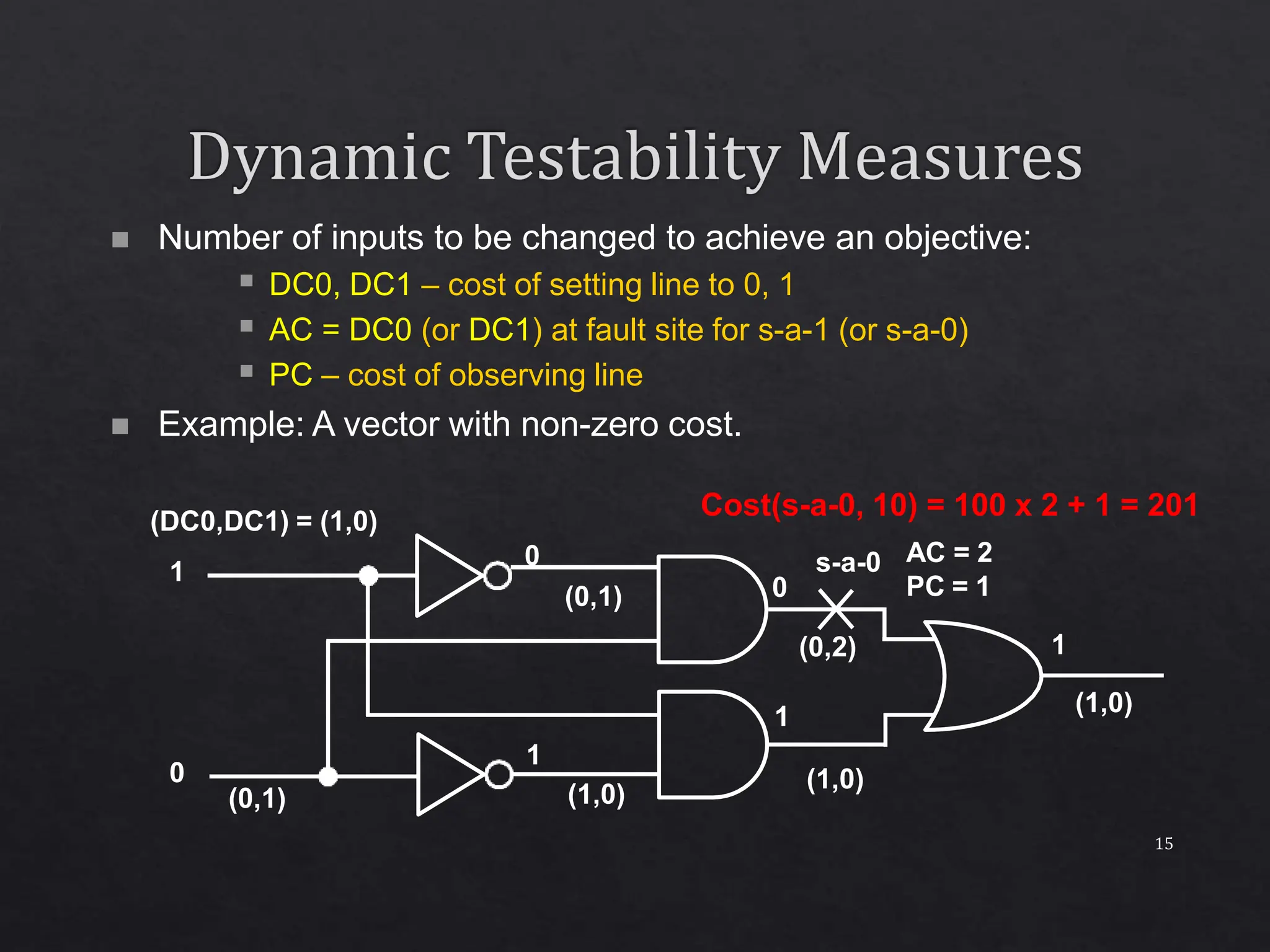
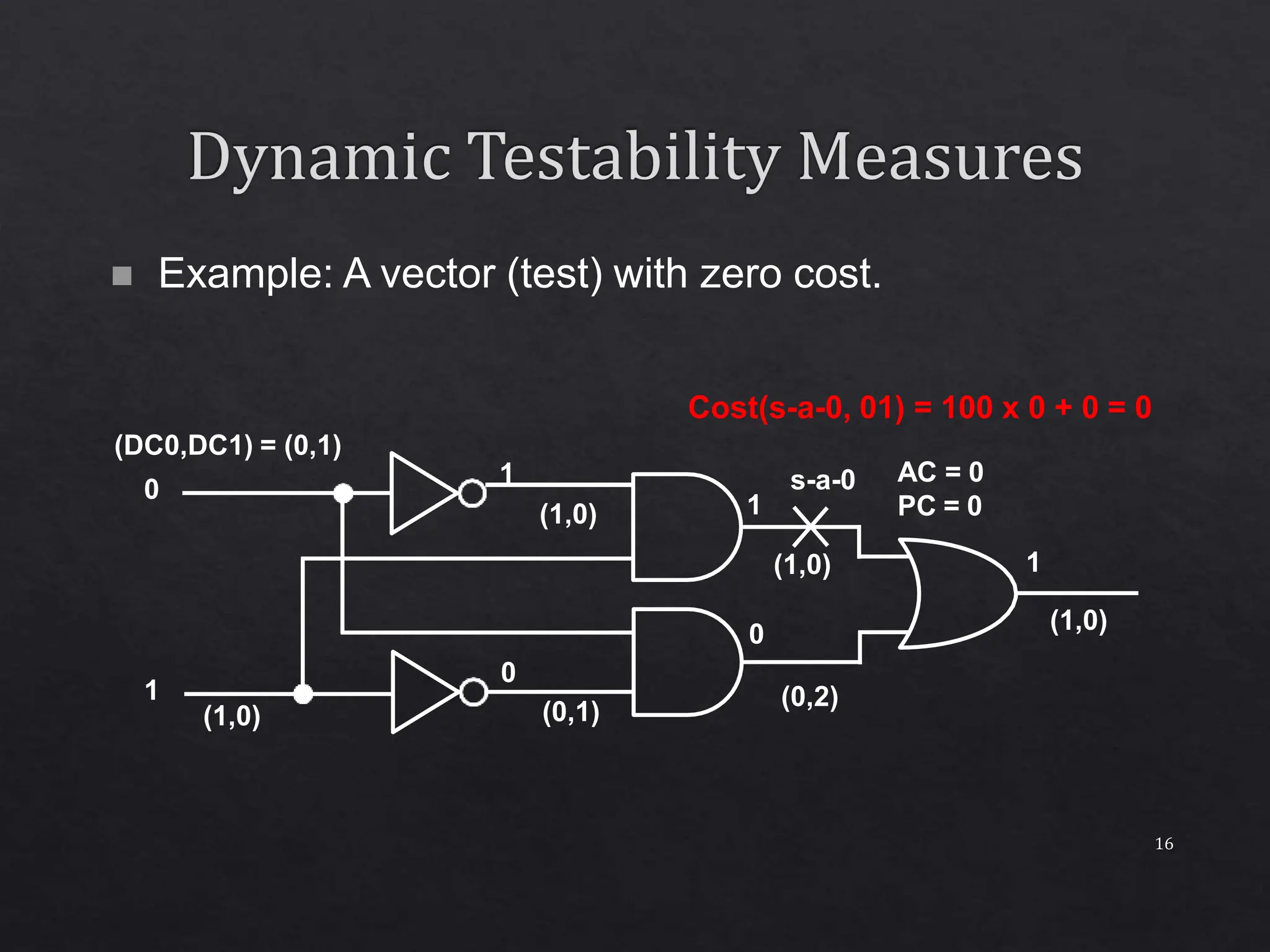
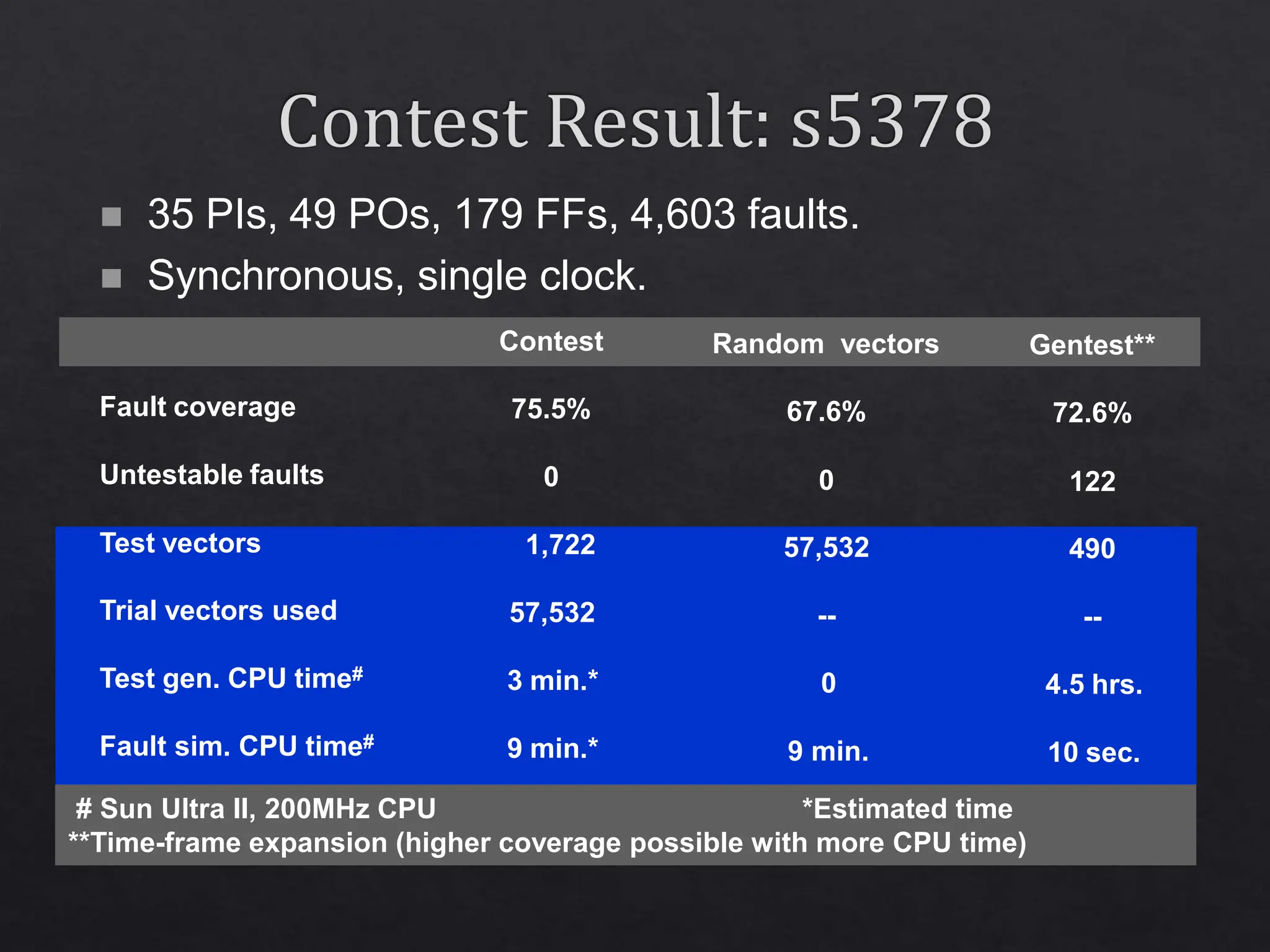
- 2. 2 A Concurrenttest generator for sequential circuit testing. Developed by Cheng & Agrawal (IEEE TCAD, 1989). Search for tests is guided by cost-functions. Three-phase test generation: Initialization No faults targeted; cost-function computed by true-value simulator. Concurrent phase All faults targeted; cost function computed by a concurrent fault simulator. Single fault phase Faults targeted one at a time; cost function computed by true- value simulation and dynamic testability analysis.
- 3. 3 10 12 10 8 7 9 5 4 3 1 Cost=0 Vectorspace Tests Initial vector(random) Trial vectors 0 0 0 1 0 0 0 0
- 4. 4 Defined forrequired objective (initialization or fault detection). Numerically grades a vector for suitability to meet the objective. Cost function = 0 for any vector that perfectly meets the objective. Computed for an input vector from true-value or fault simulation.
- 5. 5 Initialization vectorsare generated. To bring the flip-flops in the circuit to a known state irrespective of their initial states. Initialize test sequence with arbitrary, random, or given vector or sequence of vectors. Set all flip-flops in unknown (X) state, to start with. Cost function: Cost = Number of flip-flops in the unknown state Computed from true-value simulation of trial vectors
- 6. Trial vectors: A heuristically generated vector set from the previous vector(s) in the test sequence; e.g., all vectors at unit Hamming distance from the last vector may form a trial vector set. Vector selection: Add the minimum cost trial vector to the test sequence. Repeat trial vector generation and vector selection until cost becomes zero or drops below some given value. 6
- 7. 7 Initially testsequence contains vectors from Phase I. Simulate all faults and drop detected faults. Compute a distance cost function for trial vectors: Simulate all undetected faults for the trial vector. For each fault, find the shortest fault distance (in number of gates) between its fault effect and a PO. The objective in test generation is to reduce the cost by propagating the fault effect forward, gate by gate, until it reaches a primary output. Cost function is the sum of fault distances for all undetected faults.
- 8. 8 0 s-a-0 1 1 0 0 8 0 1 00 0 1 1 0 1 1 0 0 1 0 0 1 0 1 0 1 0 0 0 1 0 0 1 0 0 1 8 2 8 8 1 2 8 2 0 Initial vector Trial vectors Trial vectors Trial vectors Distance cost function for s-a-0 fault Minimum cost vector Fault detected 0 1 0 0 0 1 1 0 1 1 0 0 1 0 0 1 0 1 0 1 0 0 0 1 0 0 1 0 0 1 8 2 8 8 8 1 2 8 2 0
- 9. Trial vectors: Generate trial vectors using the unit Hamming distance or any other heuristic. Vector selection: Add the trial vector with the minimum distance cost function to test sequence. Remove faults with zero fault distance from the fault list. Repeat trial vector generation and vector selection until fault list is reduced to given size. 9
- 10. 10 The figureon next slide shows the input vector space with red dots representing tests for undetected faults from the fault list. In the beginning there may be many undetected faults. The vector space may have large clusters of tests (as shown). Starting at any initial vector, the cost function will steer the search towards large clusters. When only a few faults are left, their tests will be a few isolated vectors.
- 11.
- 12. 12 For theremaining faults, the cost function provides very little direction. Hence, a single target fault strategy may be needed.
- 13.
- 14. 14 Cost (fault,input vector) = K x AC + PC Activation cost (AC) is the dynamic controllability of the faulty line. Propagation cost (PC) is the minimum (over all paths to POs) dynamic observability of the faulty line. K is a large weighting factor, e.g., K = 100. Dynamic testability measures (controllability and observability) are specific to the present signal values in the circuit. Cost of a vector is computed for a fault from true-value simulation result. Cost = 0 means fault is detected. Trial vector generation and vector selection are similar to other phases.
- 15. 15 Number ofinputs to be changed to achieve an objective: DC0, DC1 – cost of setting line to 0, 1 AC = DC0 (or DC1) at fault site for s-a-1 (or s-a-0) PC – cost of observing line Example: A vector with non-zero cost. 1 0 1 1 1 0 (DC0,DC1) = (1,0) (0,1) 0 (0,1) (1,0) (0,2) (1,0) (1,0) s-a-0 Cost(s-a-0, 10) = 100 x 2 + 1 = 201 AC = 2 PC = 1
- 16. 16 Example: Avector (test) with zero cost. 0 1 0 0 1 1 (DC0,DC1) = (0,1) (1,0) 1 (1,0) (0,1) (1,0) (0,2) (1,0) s-a-0 Cost(s-a-0, 01) = 100 x 0 + 0 = 0 AC = 0 PC = 0
- 17. 17 More ondynamic testability measures: Unknown state – A signal can have three states. Flip-flops – Output DC is input DC, plus a large constant (say, 100), to account for time frames. Fanout – PC for stem is minimum of branch PCs. Types of circuits: Tests are generated for any circuit that can be simulated: Combinational – No clock; single vector tests. Asynchronous – No clock; simulator analyzes hazards and oscillations, 3-states, test sequences. Synchronous – Clocks specified, flip-flops treated as black- boxes, 3-states, implicit-clock test sequences.
- 18. 18 35 PIs,49 POs, 179 FFs, 4,603 faults. Synchronous, single clock. 75.5% 0 Contest Random vectors Gentest** 67.6% 72.6% 0 122 Fault coverage Untestable faults Test vectors 1,722 57,532 490 Trial vectors used 57,532 -- -- Test gen. CPU time# 3 min.* 0 4.5 hrs. Fault sim. CPU time# 9 min.* 9 min. 10 sec. # Sun Ultra II, 200MHz CPU *Estimated time **Time-frame expansion (higher coverage possible with more CPU time)