The document outlines a decision tree analysis concerning weather conditions affecting play decisions in sports, utilizing the Naive Bayes algorithm for Twitter sentiment classification. It explains the model training process, using probability to classify input tweets as positive or negative based on observed relationships between words and their respective classes. Additionally, it details the formulae for calculating the probabilities of a tweet's sentiment based on its content.

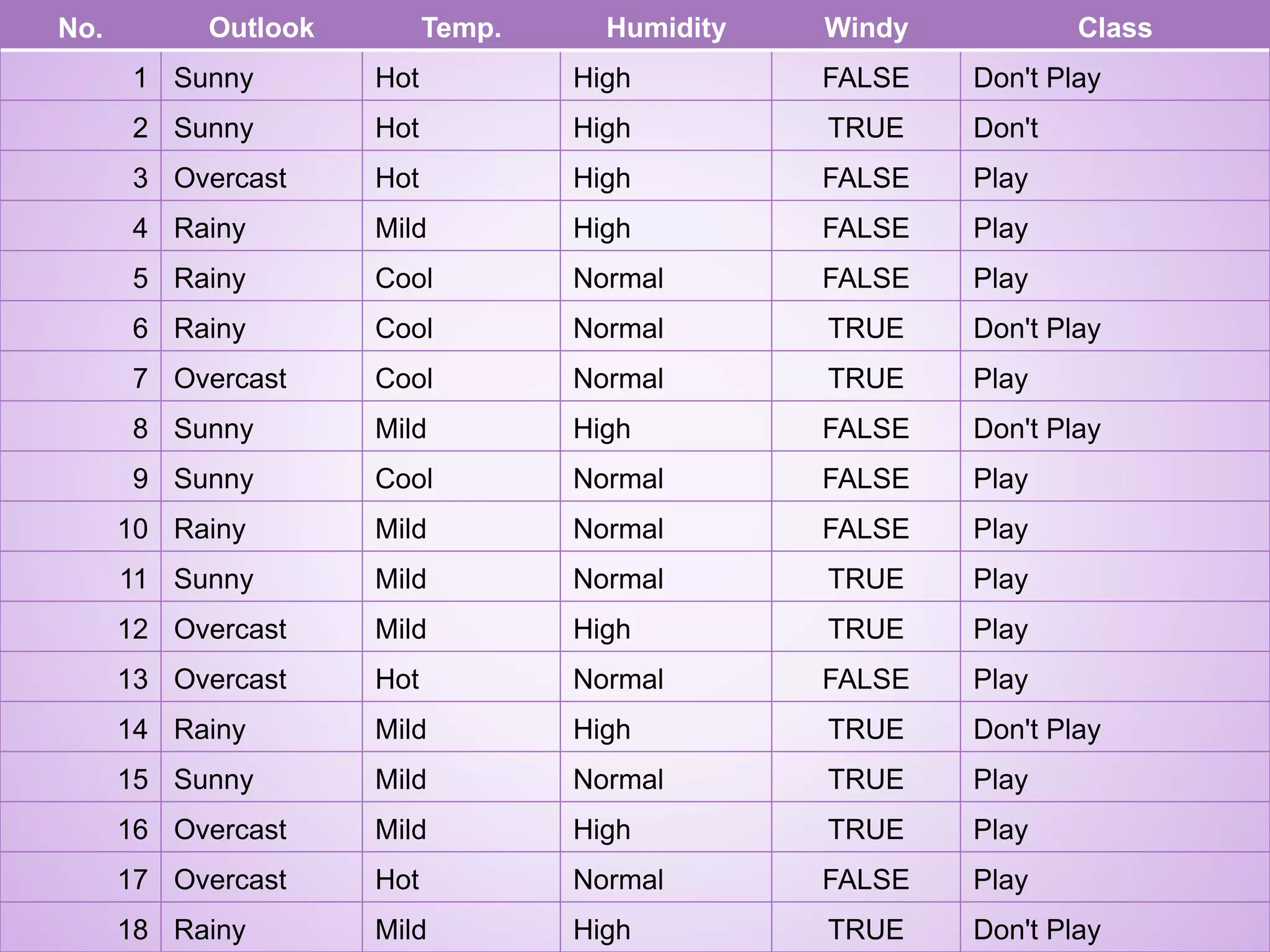
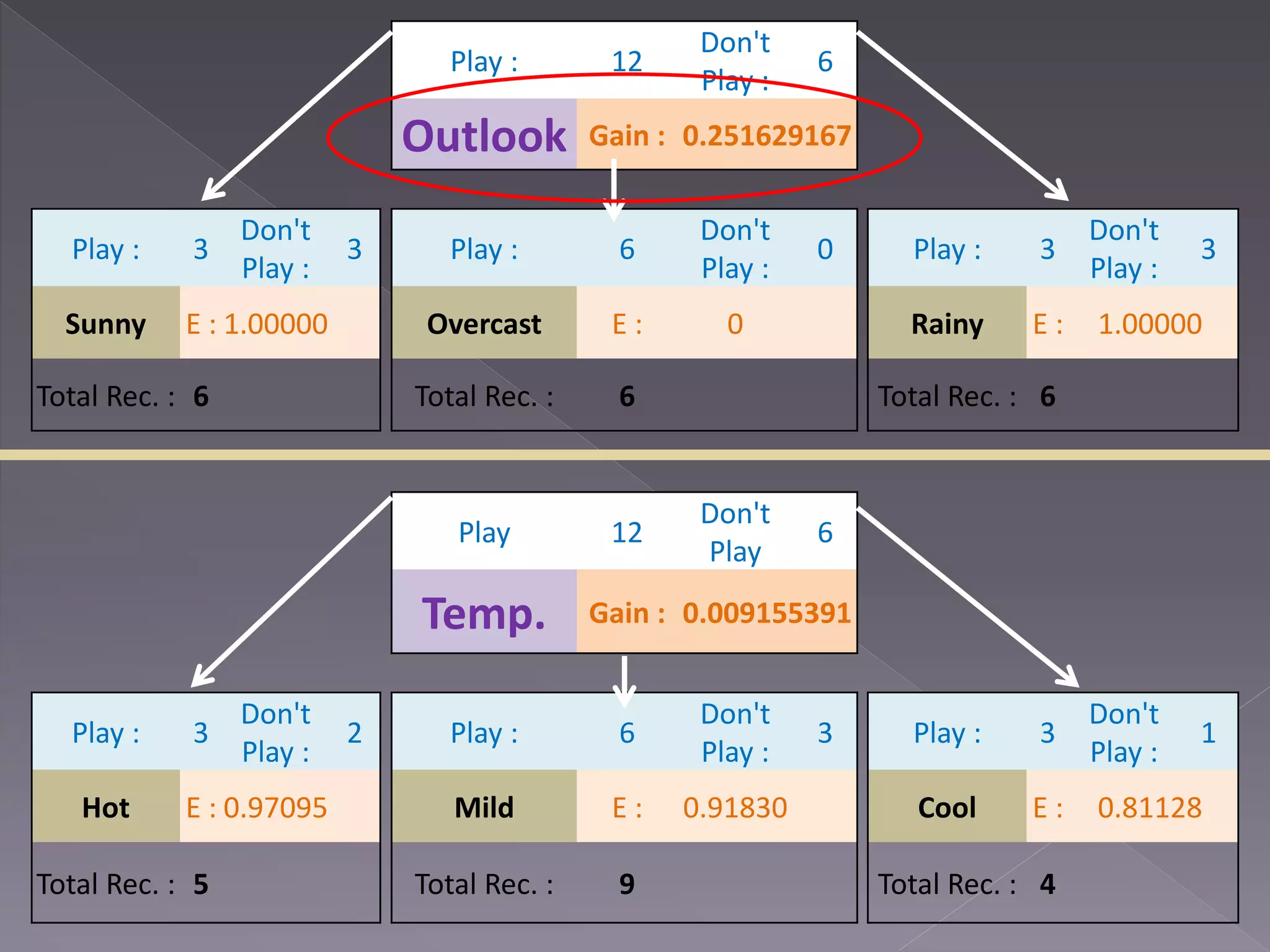

![Outlook Sunny ? Overcast [Play] Rain ?](https://image.slidesharecdn.com/mcs4102-a3-13440722-151130060339-lva1-app6891/75/Data-Analytics-and-Machine-Learning-5-2048.jpg)
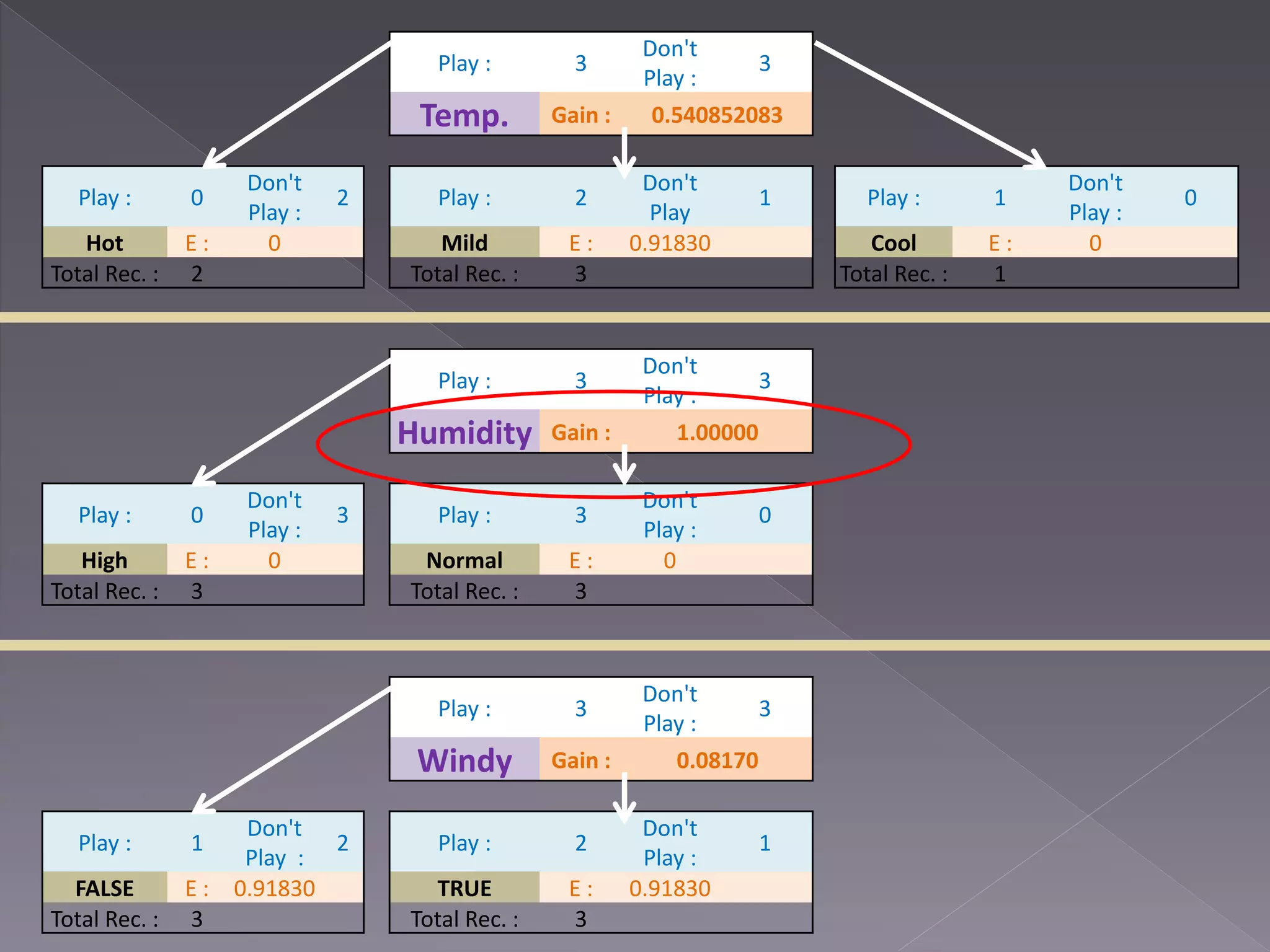
![Outlook Sunny Humidity High [Don’t Play] Normal [Play] Overcast [Play] Rain ?](https://image.slidesharecdn.com/mcs4102-a3-13440722-151130060339-lva1-app6891/75/Data-Analytics-and-Machine-Learning-7-2048.jpg)
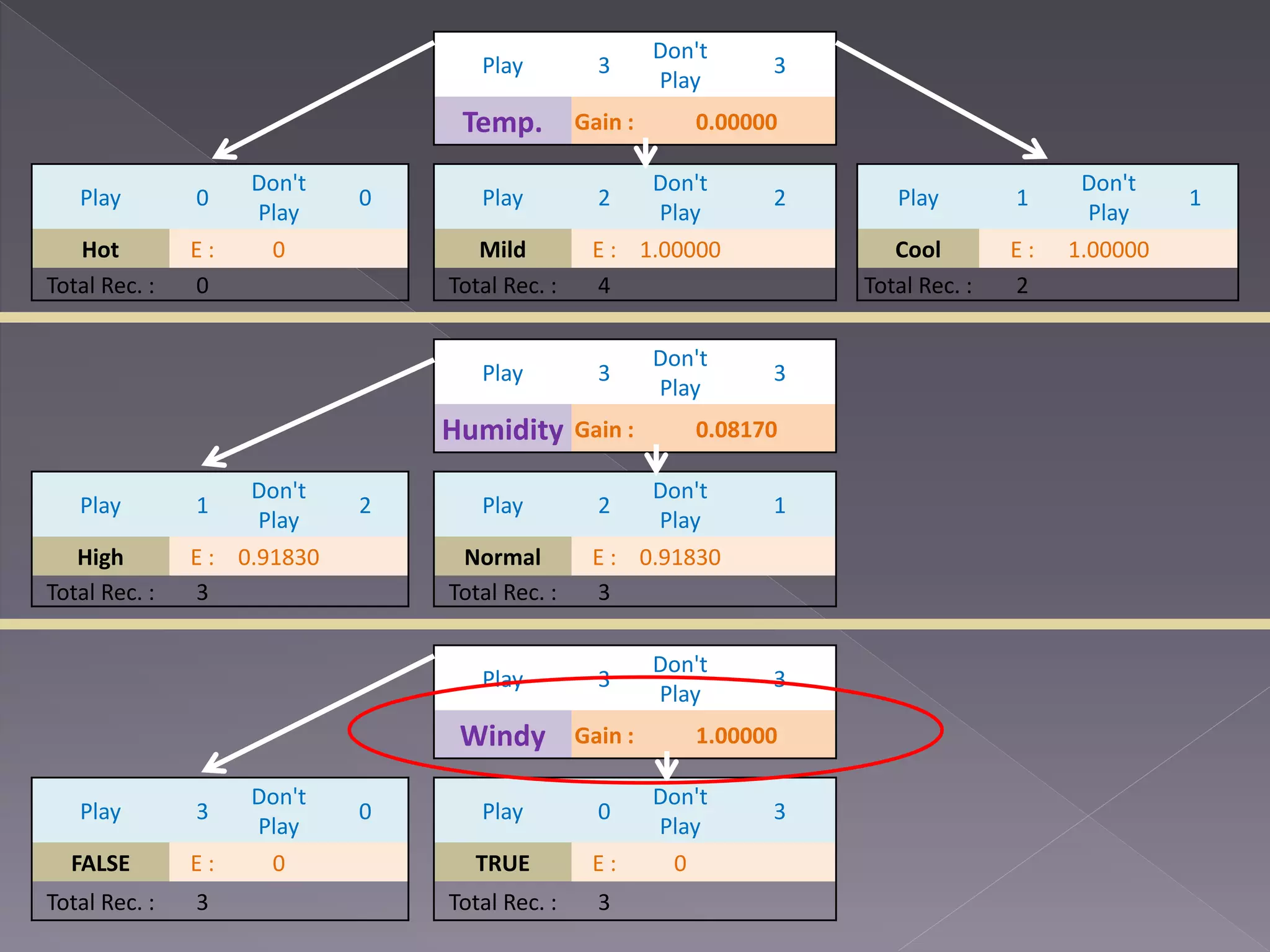
![Outlook Sunny Humidity High [Don’t Play] Normal [Play] Overcast [Play] Rain Windy False [Play] True [Don’t Play] Final Decision Tree](https://image.slidesharecdn.com/mcs4102-a3-13440722-151130060339-lva1-app6891/75/Data-Analytics-and-Machine-Learning-9-2048.jpg)










![ http://technobium.com/sentiment- analysis-using-mahout-naive-bayes/ [Online - 2015/11/11]](https://image.slidesharecdn.com/mcs4102-a3-13440722-151130060339-lva1-app6891/75/Data-Analytics-and-Machine-Learning-20-2048.jpg)