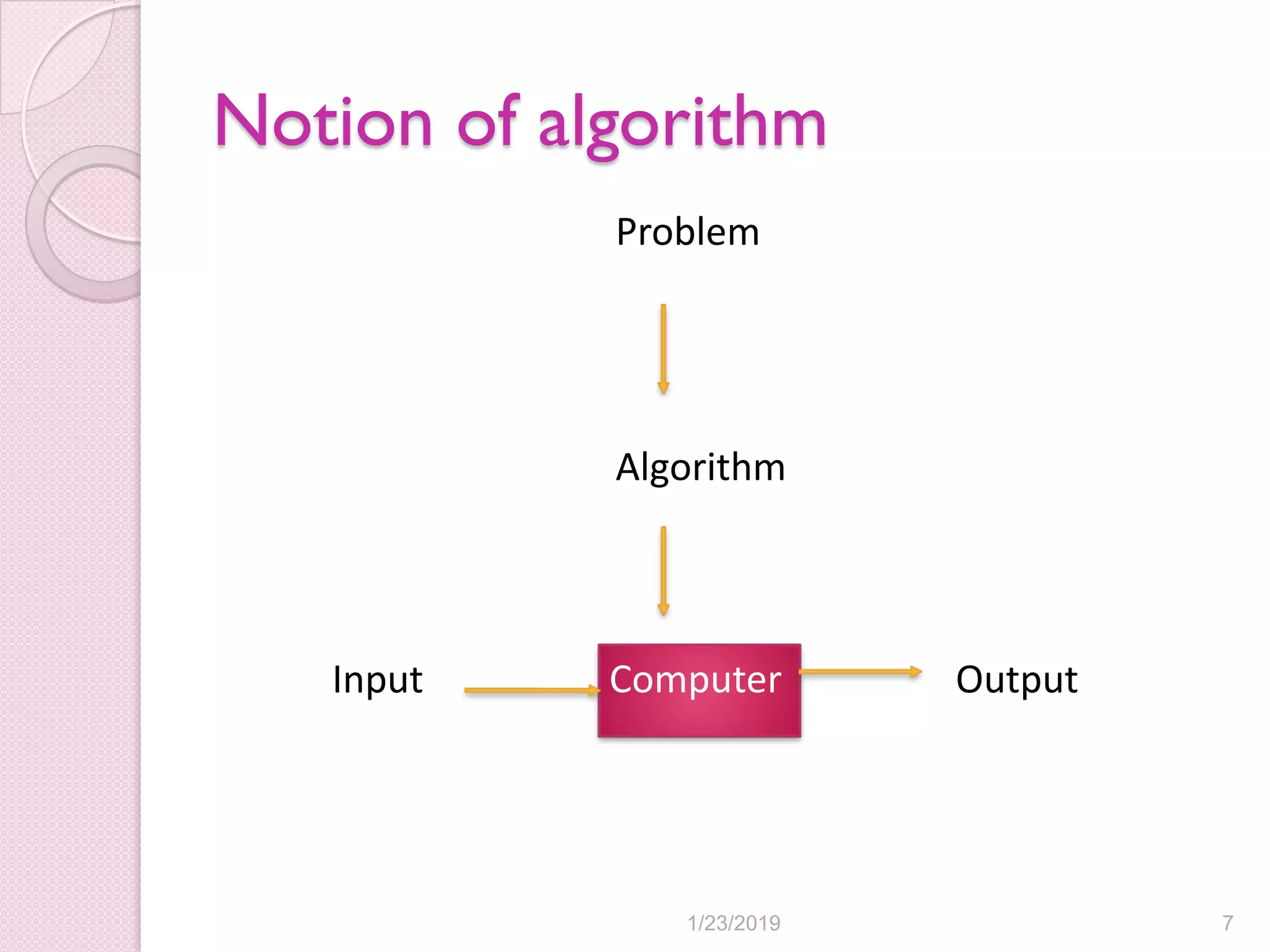
This document provides an overview of algorithms and algorithm analysis. It discusses key concepts like what an algorithm is, different types of algorithms, and the algorithm design and analysis process. Some important problem types covered include sorting, searching, string processing, graph problems, combinatorial problems, geometric problems, and numerical problems. Examples of specific algorithms are given for some of these problem types, like various sorting algorithms, search algorithms, graph traversal algorithms, and algorithms for solving the closest pair and convex hull problems.