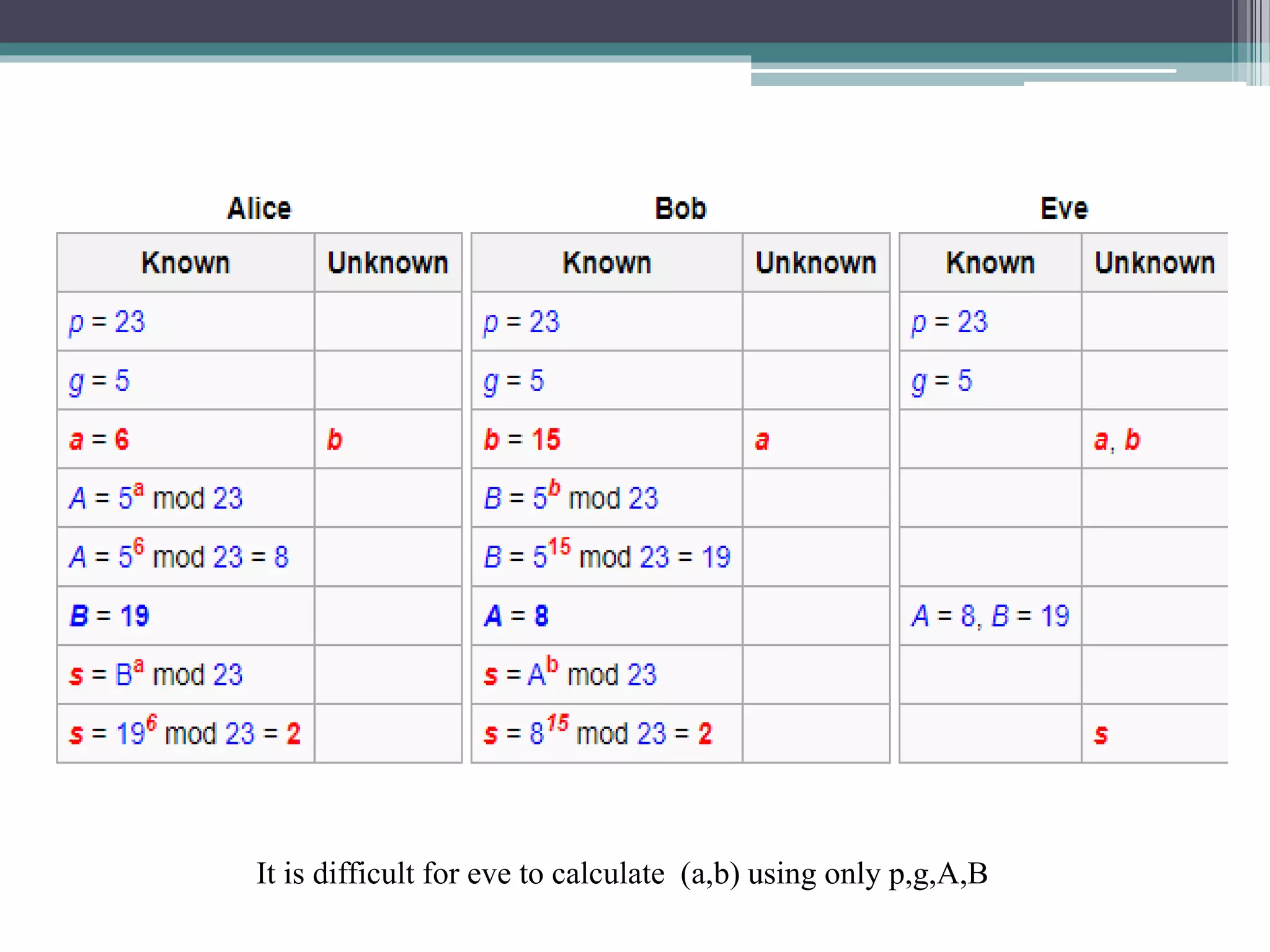
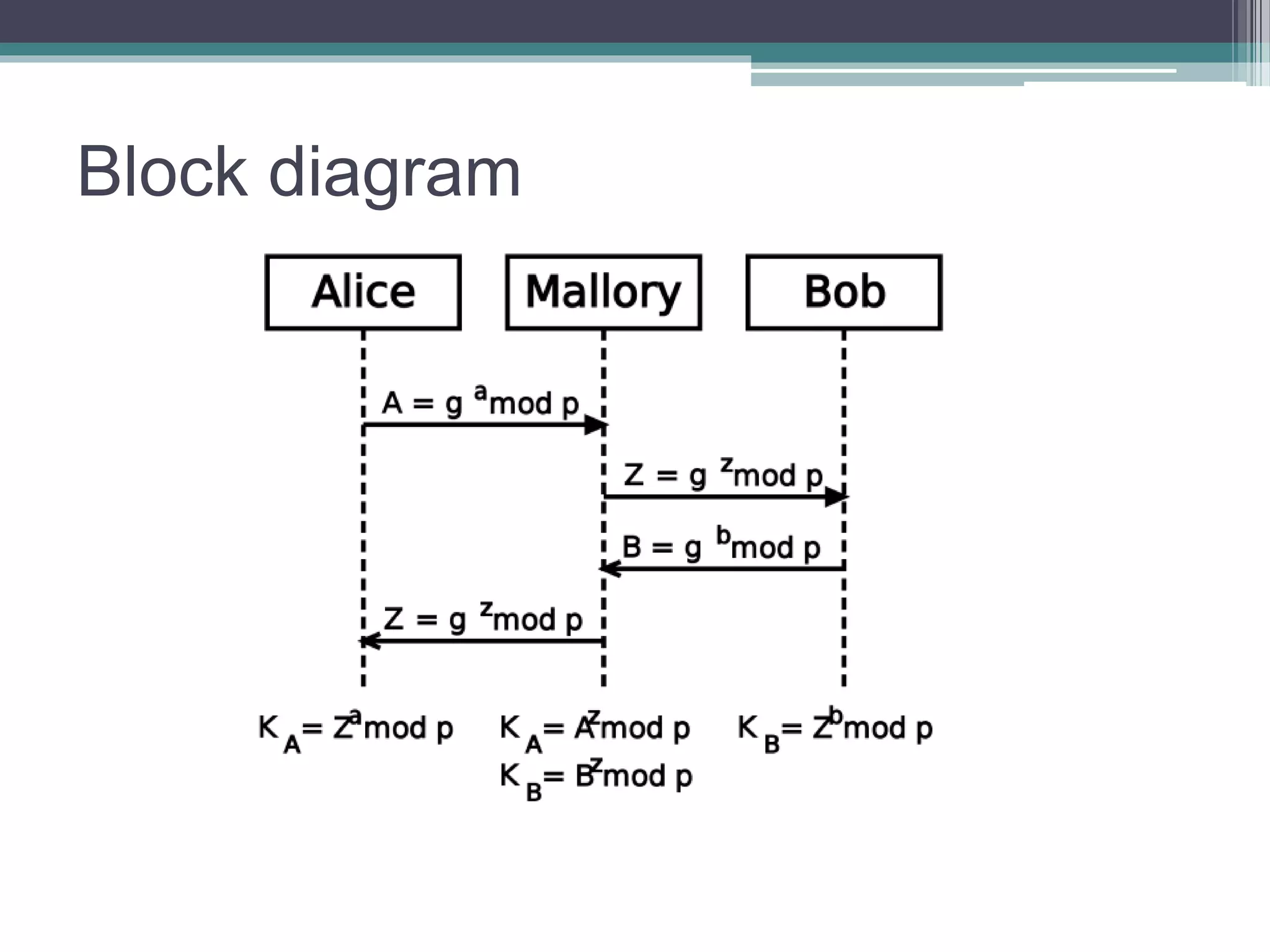
The document explains the Diffie-Hellman key exchange, a foundational method for securely sharing cryptographic keys over a public channel, introduced by Whitfield Diffie and Martin Hellman in 1976. It outlines the algorithm's mechanics, including the use of prime numbers and primitive roots, and discusses potential vulnerabilities, such as the man-in-the-middle attack. Additionally, it presents alternative solutions for secure communication, such as the key distribution center (KDC) while highlighting the challenges associated with replay attacks.