Feature selection and microarray data

On the use of feature selection to deal with the curse of dimensionality in microarray data Gianluca Bontempi gbonte@ulb.ac.be Machine Learning Group ULB, Université Libre de Bruxelles Boulevard de Triomphe - CP 212 Bruxelles, Belgium http://www.ulb.ac.be/di/mlg On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 1/2

Outline • The ULB Machine Learning Group • The feature selection problem • Feature selection and bioinformatics. • Feature selection as a stochastic optimization problem. • A blocking idea to improve wrappers • Final considerations. On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 2/2

ULB Machine Learning Group (MLG) • 7 researchers (1 prof, 6 PhD students), 4 graduate students). • Research topics: Local learning, Classification, Computational statistics, Data mining, Regression, Time series prediction, Sensor networks, Bioinformatics. • Computing facilities: cluster of 16 processors, LEGO Robotics Lab. • Website: www.ulb.ac.be/di/mlg. • Scientific collaborations in ULB: IRIDIA (Sciences Appliquées), Physiologie Moléculaire de la Cellule (IBMM), Conformation des Macromolécules Biologiques et Bioinformatique (IBMM), CENOLI (Sciences), Microarray Unit (Hopital Jules Bordet), Service d’Anesthesie (ERASME). • Scientific collaborations outside ULB: UCL Machine Learning Group (B), Politecnico di Milano (I), Universitá del Sannio (I), George Mason University (US). • The MLG is part to the "Groupe de Contact FNRS" on Machine Learning. On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 3/2

ULB-MLG: running projects 1. "Integrating experimental and theoretical approaches to decipher the molecular networks of nitrogen utilisation in yeast": ARC (Action de Recherche Concertée) funded by the Communauté Fran ˛Açaise de Belgique (2004-2009). Partners: IBMM (Gosselies and La Plaine), CENOLI. 2. "COMP2 SYS" (COMPutational intelligence methods for COMPlex SYStems) MARIE CURIE Early Stage Research Training funded by the European Union (2004-2008). Main contractor: IRIDIA (ULB). 3. "Predictive data mining techniques in anaesthesia": FIRST Europe Objectif 1 funded by the Région wallonne and the Fonds Social Européen (2004-2009). Partners: Service d’anesthesie (ERASME). 4. "AIDAR - Adressage et Indexation de Documents Multimédias Assistés par des techniques de Reconnaissance Vocale": funded by Région Bruxelles-Capitale (2004-2006). Partners: Voice Insight, RTBF, Titan. On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 4/2

Feature selection and bioinformatics • The availability of massive amounts of experimental data based on genome-wide studies has given impetus in recent years to a large effort in developing mathematical, statistical and computational techniques to infer biological models from data. • In many bioinformatics problems the number of features is signiﬁcantly larger than the number of samples (high feature to sample ratio datasets). • Examples can be found in the following bioinformatics tasks: • Breast cancer classiﬁcation on the basis of microarray data. • Network inference on the basis of microarray data. • Analysis of sequence/expression correlation. On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 5/2

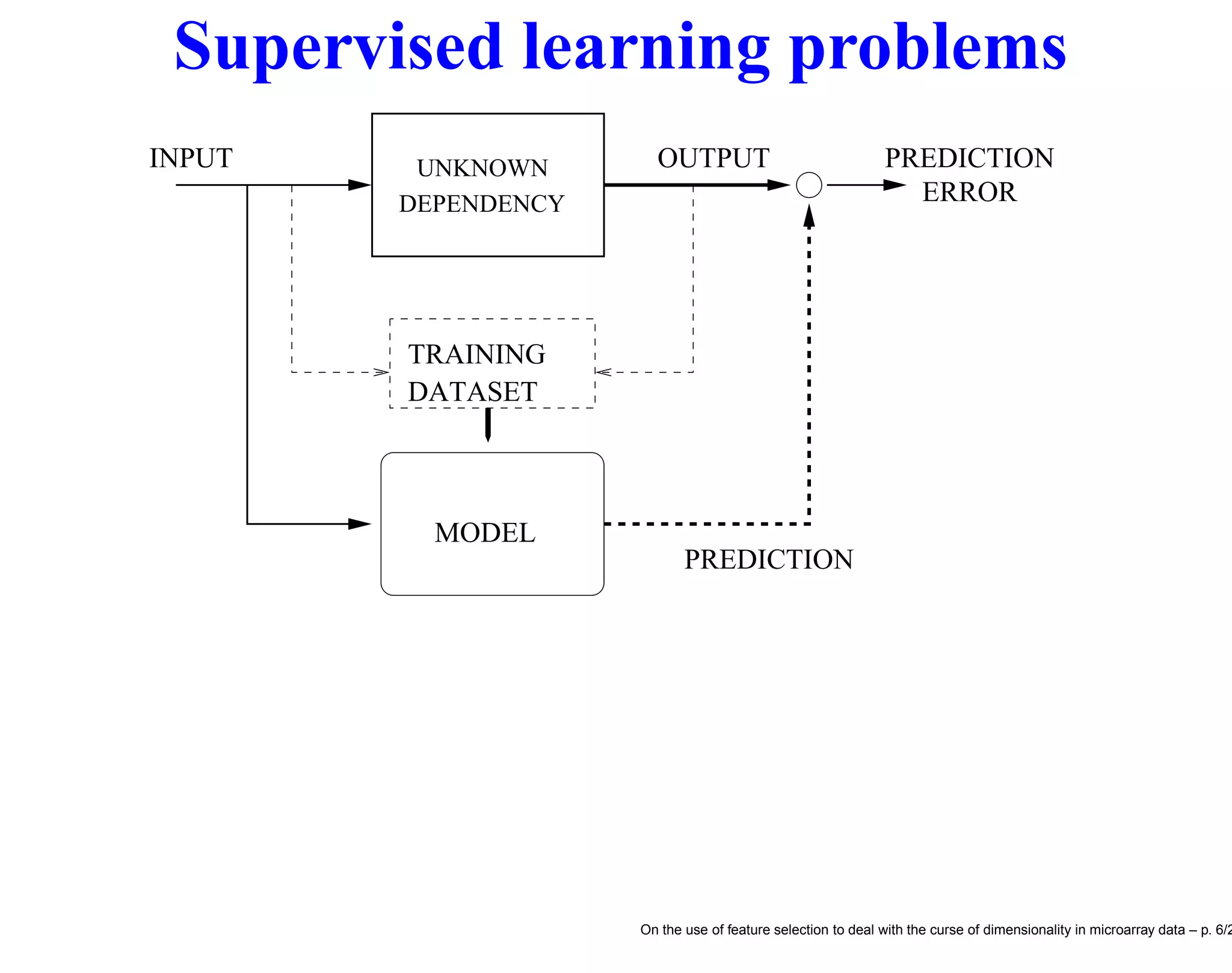
Supervised learning problems TRAINING DATASET UNKNOWN DEPENDENCY INPUT OUTPUT ERROR PREDICTION MODEL PREDICTION On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 6/2

Breast cancer classification • Systematic investigation of dependency between expression patterns of thousands of genes (measured by DNA microarrays) and specific features of phenotypic variation in order to provide the basis for an improved taxonomy of cancer. • It is expected that variations in gene expression patterns in different tumors could provide a “molecular portrait” of each tumor, and that the tumors could be classified into subtypes based solely on the difference of expression patterns. • In litterature [20] classification techniques have been applied to identify a gene expression signature strongly predictive of a short interval to distant metastases in patients without tumor cells in local lymph nodes at diagnosis. In this context the number n of features equals the number of genes (ranging from 6000 to 30000) and the number N of samples is the number of patients under examinations (about hundreds). On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 7/2

Inference of regulatory networks • Most biological regulatory processes involve intricate networks of interactions and it is now increasingly evident that predicting their behaviour and linking molecular and cellular structure to function are beyond the capacity of intuition. • Dynamic regulation models are black-box prediction models which represent gene activity with continuous values. Examples of dynamic regulation models are linear relationships of the form xi(t + δt) = f(x1(t), . . . , xn(t)), i = 1, . . . , n where xi is the expression level of the i th gene at time t. • In this case, inferring a dynamic model boils down at learning the unknown dependency on the basis of expression data. These problems demand the estimation of a number of predictive models for each gene, where the number of features equals the number of measured genes. On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 8/2

Correlating motifs and expression levels • These methods consists in directly correlating expression levels and regulatory motif present in presumptive transcription control regions [4, 19]. • In [4], the expression of a gene in a single experimental condition is modelled as a linear function E = a1S1 + a2S2 + · · · + anSn of scores computed for sequence motifs in the upstream control region. These sequence motif scores incorporate the number of occurrences of the motifs and their positions with respect to the gene’s translation start site. • In other terms the sequence motifs of a speciﬁc gene are considered as explanatory variables (feature inputs) of a statistical model which correlates sequence features and expression of the gene. For instance the number of features is n = 4m for motifs of length m. On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 9/2

Feature selection • In recent years many applications of data mining (text mining, bioinformatics, sensor networks) deal with a very large number n of features (e.g. tens or hundreds of thousands of variables) and often comparably few samples. • In these cases, it is common practice to adopt feature selection algorithms [6] to improve the generalization accuracy. • There are many potential beneﬁts of feature selection: • facilitating data visualization and data understanding, • reducing the measurement and storage requirements, • reducing training and utilization times, • defying the curse of dimensionality to improve prediction performance. On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 10/2

The two issues of f.s. Two main issues make the problem of feature selection a highly challenging task: Search in a high dimensional space: this is known to be a NP-hard problem. Assessment on the basis of a small set of samples: this is made difﬁcult by the high ratio between the dimensionality of the problem and the number of measured samples. On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 11/2

Approaches to f.s. Three are the main approaches to feature selection: Filter methods: they are preprocessing methods. They attempt to assess the merits of features from the data, ignoring the effects of the selected feature subset on the performance of the learning algorithm. Examples are methods that select variables by ranking them through compression techniques (like PCA) or by computing correlation with the output (e.g. Gram-Schmidt, mutual information). Wrapper methods: these methods assess subsets of variables according to their usefulness to a given predictor. The method conducts a search for a good subset using the learning algorithm itself as part of the evaluation function. The problem boils down to a problem of stochastic state space search. Example are the stepwise methods proposed in linear regression analysis. Embedded methods: they perform variable selection as part of the learning procedure and are usually speciﬁc to given learning machines. Examples are classiﬁcation trees, regularization techniques (e.g. lasso). On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 12/2

Wrapper selection • The wrapper search can be seen as a search in a space S = {0, 1}n where a generic vector s ∈ S is such that sj =    0 if the input j does NOT belong to the set of features 1 if the input j belongs to the set of features • We look for the optimal vector s∗ ∈ {0, 1}n such that s∗ = arg min s∈S Miscl(s) where Miscl(s) is the generalization error of the model based on the set of variables described by s. • the number of vectors in S is equal to 2n . • for moderately large n, the exhaustive search is no more possible. On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 13/2

Wrapping search strategies Various methods have been developed for evaluating only a small number of variables by either adding or deleting one variable at a time. We consider here some greedy strategies: Forward selection: the procedure starts with no variables. The first input selected is the one which allows the lowest misclassification error. The second input selected is the one that, together with the first, has the lowest error, and so on, till when no improvement is made. Backward selection: it works in the opposite direction of the forward approach. We begin with a model that contains all the n variables. The first input to be removed is the one that allows the lowest generalization error. Stepwise selection: it combines the previous two techniques, by testing for each set of variables, first the removal of features beloning to the set, then the addition of variables not in the set. On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 14/2

Open issues • The wrapper approach to feature selection requires the assessment of several subset alternatives and the selection of the one which is expected to have the lowest misclassiﬁcation error during generalization. • To tackle this problem, we need to perform a search procedure in a very large space of subsets of features aiming to minimize a leave-one-out or more in general a cross-validation criterion. • This practice can lead to a strong bias selection in the case of high dimensionality problems. • The feature selection problem may be formulated in terms of a stochastic optimization problem where the selection of the best subset has to be based on a sample estimate Miscl. On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 15/2

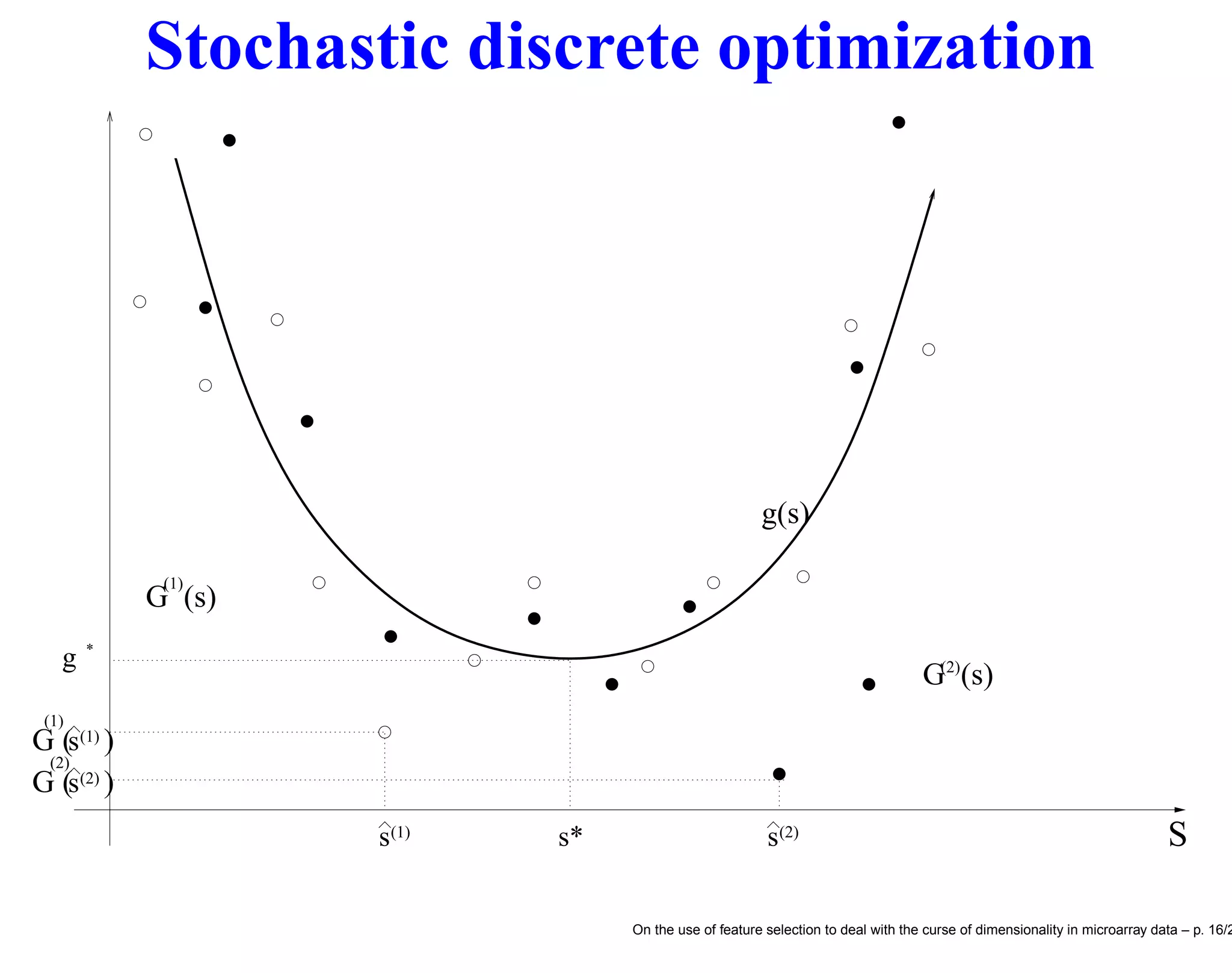
Stochastic discrete optimization (2) s(2) s(2) s(1) s(1) s* g(s) G (s)(2)g * S G (s) (1) G ( ) G ( ) (1) On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 16/2

F.s. and stochastic discrete optimization We may formulate the feature selection problem as a discrete optimization problem [10] s∗ = arg min s∈S Miscl(s) (1) be the optimal solution of the feature selection problem and the relative optimal generalization error, respectively. • Unfortunately the Miscl for a given s is not directly measurable but can only be estimated by the quantity Miscl(s) which is an unbiased estimator of Miscl(s). • The wrapper approach to feature selection aims to return the minimum ˆs of a cross-validation criterion Miscl(s) ˆs = arg min s∈S Miscl(s) (2) On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 17/2

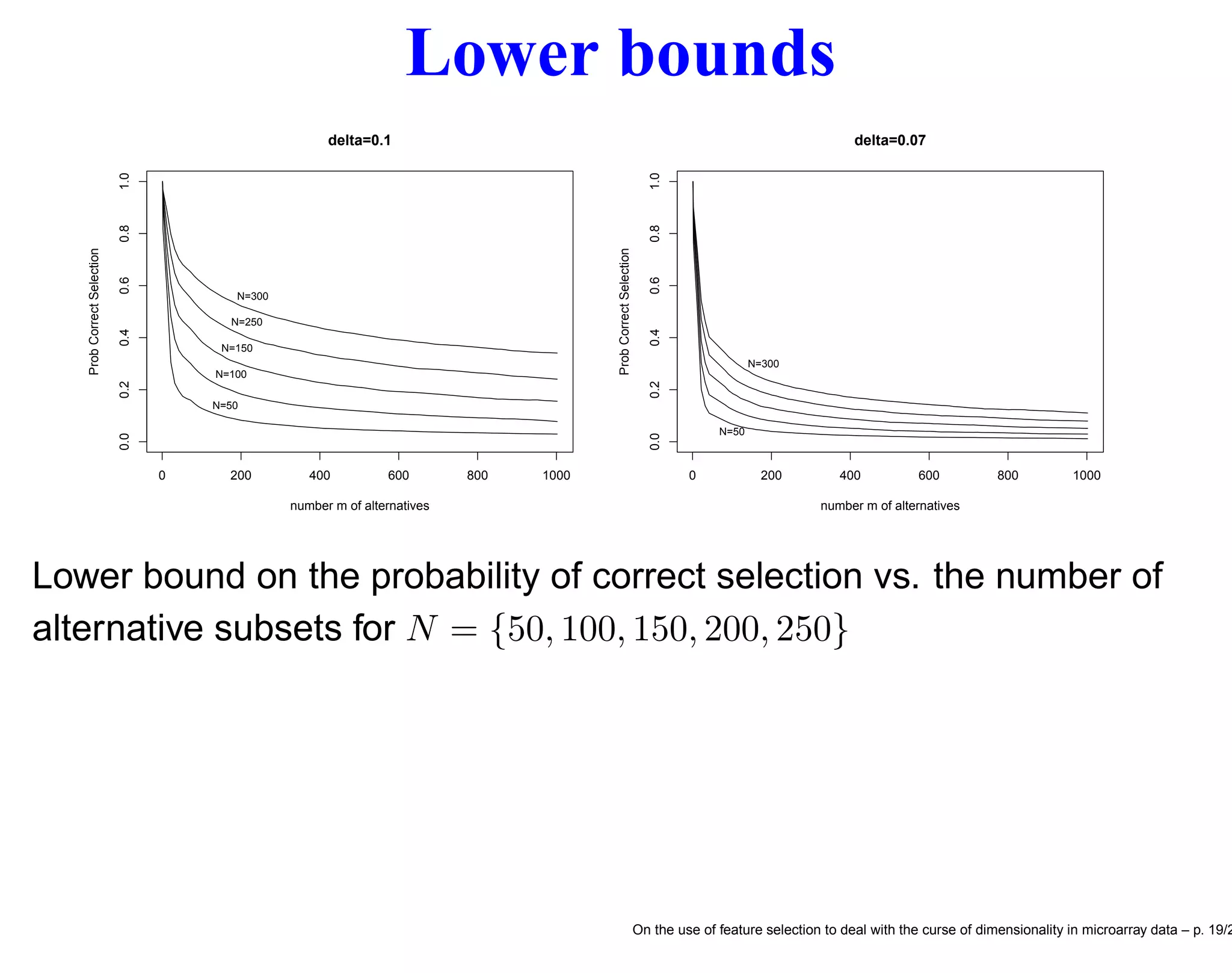
Probability of correct selection Let Miscl(sj), j = 1, . . . , m be the (unknown) misclassiﬁcation error of the jth feature subset and assume that the subsets are indexed in such a way that Miscl(sm) ≤ Miscl(sm−1) ≤ · · · ≤ Miscl(s1) so that (unknown to us) the feature set sm = s∗ is the best one. Assume also that Miscl(sm−1) − Miscl(sm) ≥ δ > 0. Prob {ˆs = s∗ } = Prob Misclm < Misclj, ∀j = m ≥ ≥ Prob Zj < δ σm 4/N , ∀j = m where Misclj − Misclm ≥ δ > 0 for all j = 1, . . . , m − 1 and the random vector (Z1, Z2, . . . , Zm−1) has a multivariate Normal distribution with means 0, variances 1 and common pairwise correlations 1/2 [9]. On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 18/2

Lower bounds 0 200 400 600 800 1000 0.00.20.40.60.81.0 number m of alternatives ProbCorrectSelection N=50 N=100 N=150 N=250 N=300 delta=0.1 0 200 400 600 800 1000 0.00.20.40.60.81.0 number m of alternatives ProbCorrectSelection N=50 N=300 delta=0.07 Lower bound on the probability of correct selection vs. the number of alternative subsets for N = {50, 100, 150, 200, 250} On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 19/2

Our proposal • We propose an original blocking strategy for improving feature selection which aggregates in a paired way the validation outcomes of several learning algorithms to assess a gene subset and compare it to others. • This is new with respect to conventional wrappers which commonly adopt only one learning algorithm to evaluate the relevance of a given set of variables. • The rationale of the approach is that by increasing the amount of experimental conditions under which we validate a feature subset, we can lessen the problems related to the scarcity of samples and consequently come up with a better selection. • The idea is quite simple: if we want to search for the best subset of features, this subset should appear among the best ones whatever the learning algorithm is. So far, the methods in feature selection end up with one of these two ways: either avoid any learning algorithm (as in the case of ﬁlters), either restrict themselves to consider only a speciﬁc one (as in conventional wrapper). What we advocate here is that by using more than one algorithm in a feature selection task we may improve the robustness of the selection procedure. On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 20/2

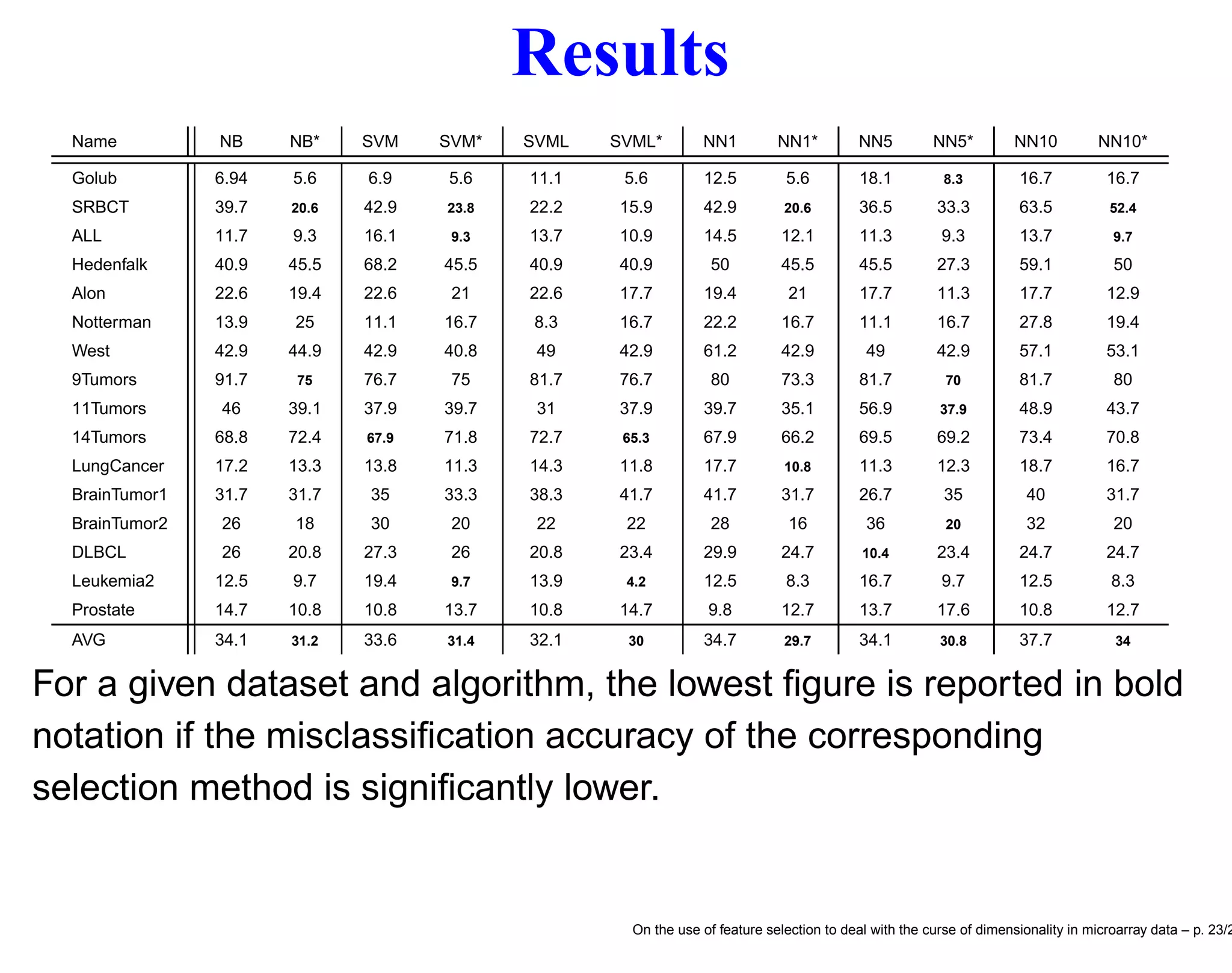
Datasets Name Reference Platform N n C Golub [5] Affy hu6800 72 7129 2 SRBCT [8] cDNA 63 2308 4 ALL [22] Affy hgu95av2 248 12558 6 Hedenfalk [7] cDNA 22 3226 3 Alon [1] Affy hum6000 62 2000 2 Notterman [11] Affy hu6800 36 7457 2 West [21] Affy hu6800 49 7129 4 9Tumors [17] Affy hu6800 60 7129 9 11Tumors [18] Affy hgu95av2 174 12533 11 14Tumors [14] Affy hu35ksubacdf 308 15009 26 LungCancer [3] Affy hgu95av2 203 12600 5 BrainTumor1 [13] Affy hu6800 60 7129 5 BrainTumor2 [12] Affy hgu95av2 50 12625 4 DLBCL [15] Affy hu6800 77 7129 2 Leukemia2 [2] Affy hgu95a 72 12582 3 Prostate [16] Affy hgu95av2 102 12600 2 On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 21/2

Experimental session • A first dimensionality reduction step is carried out by ranking the variables according to an univariate classification and by selecting the first 1000 gene probes. • A three-fold cross-validation strategy is used to measure the generalization accuracy of the two competitive feature selection strategies. Note that unlike conventional cross-validation we use here only one third of the samples for training and two third of the samples for test. • Given a third of the samples, we run both a conventional forward selection with a given learning algorithm and an enhanced forward selection based on K = 6 learning algorithms implemented by the R statistical software. The six algorithms are: a Naive Bayes (NB), a Support Vector Machine with a radial Gaussian kernel (SVM), a Support Vector Machine with a linear kernel (SVML), a Nearest Neighbour with one neighbor (NN1), a Nearest Neighbor with 5 neighbors (NN5) and a Nearest Neighbor with 10 neighbors (NN10). On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 22/2

Results Name NB NB* SVM SVM* SVML SVML* NN1 NN1* NN5 NN5* NN10 NN10* Golub 6.94 5.6 6.9 5.6 11.1 5.6 12.5 5.6 18.1 8.3 16.7 16.7 SRBCT 39.7 20.6 42.9 23.8 22.2 15.9 42.9 20.6 36.5 33.3 63.5 52.4 ALL 11.7 9.3 16.1 9.3 13.7 10.9 14.5 12.1 11.3 9.3 13.7 9.7 Hedenfalk 40.9 45.5 68.2 45.5 40.9 40.9 50 45.5 45.5 27.3 59.1 50 Alon 22.6 19.4 22.6 21 22.6 17.7 19.4 21 17.7 11.3 17.7 12.9 Notterman 13.9 25 11.1 16.7 8.3 16.7 22.2 16.7 11.1 16.7 27.8 19.4 West 42.9 44.9 42.9 40.8 49 42.9 61.2 42.9 49 42.9 57.1 53.1 9Tumors 91.7 75 76.7 75 81.7 76.7 80 73.3 81.7 70 81.7 80 11Tumors 46 39.1 37.9 39.7 31 37.9 39.7 35.1 56.9 37.9 48.9 43.7 14Tumors 68.8 72.4 67.9 71.8 72.7 65.3 67.9 66.2 69.5 69.2 73.4 70.8 LungCancer 17.2 13.3 13.8 11.3 14.3 11.8 17.7 10.8 11.3 12.3 18.7 16.7 BrainTumor1 31.7 31.7 35 33.3 38.3 41.7 41.7 31.7 26.7 35 40 31.7 BrainTumor2 26 18 30 20 22 22 28 16 36 20 32 20 DLBCL 26 20.8 27.3 26 20.8 23.4 29.9 24.7 10.4 23.4 24.7 24.7 Leukemia2 12.5 9.7 19.4 9.7 13.9 4.2 12.5 8.3 16.7 9.7 12.5 8.3 Prostate 14.7 10.8 10.8 13.7 10.8 14.7 9.8 12.7 13.7 17.6 10.8 12.7 AVG 34.1 31.2 33.6 31.4 32.1 30 34.7 29.7 34.1 30.8 37.7 34 For a given dataset and algorithm, the lowest figure is reported in bold notation if the misclassification accuracy of the corresponding selection method is significantly lower. On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 23/2

Some considerations • Bioinformatics applications are known to be characterized by highly noisy data. • The huge size of the feature space compared to the number of samples makes hard the problem in terms of: Optimization techniques to explore the feature space. Large variance of the resulting model. • Biologists asks for prediction accuracy but mainly for causual intepretation (gene signature). • Biologists are scared of unstable feature selection procedures which change the sets of relevant genes simply by adding more observations. Examples are clinical study with different populations of patients. • Filtering techniques are computational efficient and robust against overfitting. They may introduce bias but may have considerably less variance. • Literature have been inflationed by over-optimistic results. On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 24/2

Closing remarks • Let us not forget that any learner is an estimator and as such any outcome it returns, is a random variable. • If the outcome of our feature selection technique is a set of variables, this set is also a random set. • Data miners are used to return conﬁdence interval on accuracy. • They should start returning conﬁdence intervals also on feature (gene) subsets. On the use of feature selection to deal with the curse of dimensionality in microarray data – p. 25/2

References [1] U. Alon, N. Barkai, D.A. Notterman, K. Gish, S. Ybarra, D. Mack, and A.J. Levine. Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proc. of the National Academy of Sci- ences, 96(10):6745–6750, 1999. [2] S.A. Armstrong, J.E. Staunton, L.B. Silverman, R. Pieters, M.L. den Boer, M.D. Minden, S.E. Sallan, E.S. Lander, T.R. Golub, and S.J. Korsmeyer. Mll translocations specify a distinct gene expression profile that distinguishes a unique leukemia. Nature Genetics, 30(1):41–47, 2002. [3] A. Bhattacharjee, W.G. Richards, J. Staunton, C. Li, S. Monti, P. Vasa, C. Ladd, J. Beheshti, R. Bueno, M. Gillette, M. Loda, G. Weber, E.J. Mark, E.S. Lander, W. Wong, B.E. Johnson, T.R. Golub, D.J. Sugarbaker, and M. Meyerson. Classification of human lung carcinomas by mrna expression profiling reveals distinct adenocarcinoma subclasses. Proc Natl Acad Sci U S A., 98(24):13790–13795, 2001. [4] H.J. Bussemaker, H. Li, and E. D. Siggia. Regulatory element detection using correlation with expression. Nature Genetics, 27:167–171, 2001. [5] T. R. Golub, D. K. Slonin, P. Tamayo, C. Huard, and M. Gaasen- beek. Molecular clssification of cancer: Class discovery and class prediction by gene expression monitoring. Science, 286:531–537, 1999. 25-1

[6] I. Guyon and A. Elisseeff. An introduction to variable and feature selection. Journal of Machine Learning Research, 3:1157–1182, 2003. [7] I. Hedenfalk, D. Duggan, Y. Chen, M. Radmacher, M. Bittner, R. Simon, P. Meltzer, B. Gusterson, M. Esteller, O.P. Kallioniemi, B. Wilfond, A. Borg, and J. Trent. Gene expression profiles in hereditary breast cancer. New Engl. Jour. Medicine, 344(8):539– 548, 2001. [8] J. Khan, J. S. Wei, and M. Ringner. Clasification and diagnostic prediction of cancers using gene expression profiling and artifi- cial neural networks. Nature Medicine, 7(6):673–679, 2001. [9] S. H. Kim and B. L. Nelson. Handbooks in Operations Research and Management Science, chapter Selecting the Best System. Elsevier, 2005. [10] A. J. Kleywegt, A. Shapiro, and T. Homem de Mello. The sample average approximation method for stochastic discrete optimization. SIAM Journal of Optimization, 12:479–502, 2001. [11] D.A. Notterman, U. Alon, A.J. Sierk, and A.J. Levine. Transcrip- tional gene expression profiles of colorectal adenoma, adenocarcinoma and normal tissue examined by oligonucleotide arrays. Cancer Research, 6:3124–3130, 2001. [12] C. L. Nutt, D.R. Mani, R.A. Betensky, P. Tamayo, J.G. Cairncross, C. Ladd, U. Pohl, C. Hartmann, M.E. McLaughlin, T.T. Batche- lor, P.M. Black, A. von Deimling, S.L. Pomeroy, T.R. Golub, and D.N. Louis. Gene expression-based classification of malignant 25-2

gliomas correlates better with survival than histological classiﬁ- cation. Cancer Research, 63(7):1602–1607, 2003. [13] S. L. Pomeroy, P. Tamayo, M. Gaasenbeek, L.M. Sturla, Angelo M, McLaughlin ME, Kim JY, Goumnerova LC, Black PM, Lau C, Allen JC, Zagzag D, Olson JM, Curran T, Wetmore C, Biegel JA, Poggio T, Mukherjee S, Rifkin R, Califano A, Stolovitzky G, Louis DN, Mesirov JP, Lander ES, and Golub TR. Prediction of cen- tral nervous system embryonal tumour outcome based on gene expression. Nature, 415(6870):436–442, 2002. [14] S. Ramaswamy, P. Tamayo, R. Rifkin, S. Mukherjee, C.H. Yeang, M. Angelo, C. Ladd, M. Reich, E. Latulippe, J.P. Mesirov, T. Pog- gio, W. Gerald, M. Loda, E.S. Lander, and T.R. Golub. Multiclass cancer diagnosis using tumor gene expression signatures. Proc Natl Acad Sci U S A, 98(26):15149–15154, 2001. [15] M.A. Shipp, K.N. Ross, P. Tamayo, A.P. Weng, J.L. Kutok, R.C. Aguiar, M. Gaasenbeek, M. Angelo, M. Reich, G.S. Pinkus, T.S. Ray, M.A. Koval, K.W. Last, A. Norton, T.A. Lister, J. Mesirov andD.S. Neuberg, E.S. Lander, J.C. Aster, and T.R. Golub. Diffuse large b-cell lymphoma outcome prediction by gene- expression proﬁling and supervised machine learning. Nature Medicine, 8(1):68–74, 2002. [16] D. Singh, P.G. Febbo, K. Ross, D.G. Jackson, J. Manola, C. Ladd, P. Tamayo, A.A. Renshaw, A.V. D’Amico, J.P. Richie, E.S. Lander, M. Loda, P.W. Kantoff, T.R. Golub, and W.R. Sellers. Gene expression correlates of clinical prostate cancer behavior. Cancer Cell., 1(2):203–209, 2002. 25-3

[17] J.E. Staunton, D.K. Slonim, H.A. Coller, P. Tamayo, M.J Angelo, J. Park, U. Scherf, J.K. Lee, W.O. Reinhold, J.N. Weinstein, J.P. Mesirov, E.S. Lander, and T.R. Golub. Chemosensitivity prediction by transcriptional profiling. Proc Natl Acad Sci U S A., 98(19):10787–10792, 2001. [18] A.I. Su, J.B. Welsh, L.M. Sapinoso, S.G. Kern, P. Dimitrov, H. Lapp, P.G. Schultz, S.M. Powell, C.A. Moskaluk, H.F. Frier- son Jr, and G. M. Hampton G. Molecular classification of human carcinomas by use of gene expression signatures. Cancer Re- search, 61(20):7388–7393, 2001. [19] S. L.M. van der Keles and M. B. Eisen. Identification of regulatory elements using a feature selection method. Bioinformatics, 18:1167–1175, 2002. [20] L. J. van’t Veer, H. Dai, and M. J. van de Vijver. Gene expression profiling predicts clinical outcome of breast cancer. Nature, 415:530–536, 2002. [21] M. West, C. Blanchette, H. Dressman, E. Huang, S. Ishida, R. Spang, H. Zuzan, J. R. Marks, and J. R. Nevins. Predicting the clinical status of human breast cancer by using gene expression profiles. Proc. Nat. Acad. Sci., 98(20):11462–11467, 2001. [22] E.J. Yeoh, M.E. Ross, S.A. Shurtleff, W.K. Williams, D. Patel, R. Mahfouz, F.G. Behm, S.C. Raimondi, M.V. Relling, and A. Pa- tel. Classification, subtype discovery, and prediction of outcome in pediatric lymphoblastic leukemia by gene expression profiling. Cancer Cell, 1:133–143, 2002. 25-4

Feature selection and microarray data

More Related Content

What's hot

Similar to Feature selection and microarray data

More from Gianluca Bontempi

Recently uploaded

Feature selection and microarray data