Fp in scala part 1

FP in Scala into the rabbit hole (part 1)

Introduction ● This is mostly about Functional programming ● This is not about Scala language, but we will go through them when we are run into language features ● A lot of my examples here comes from the book Functional programming in Scala

Functional Programming One famous Chinese saying said: As small the sparrow is, it has all the vital organs a life needs. Let begin with a small “Sparrow”

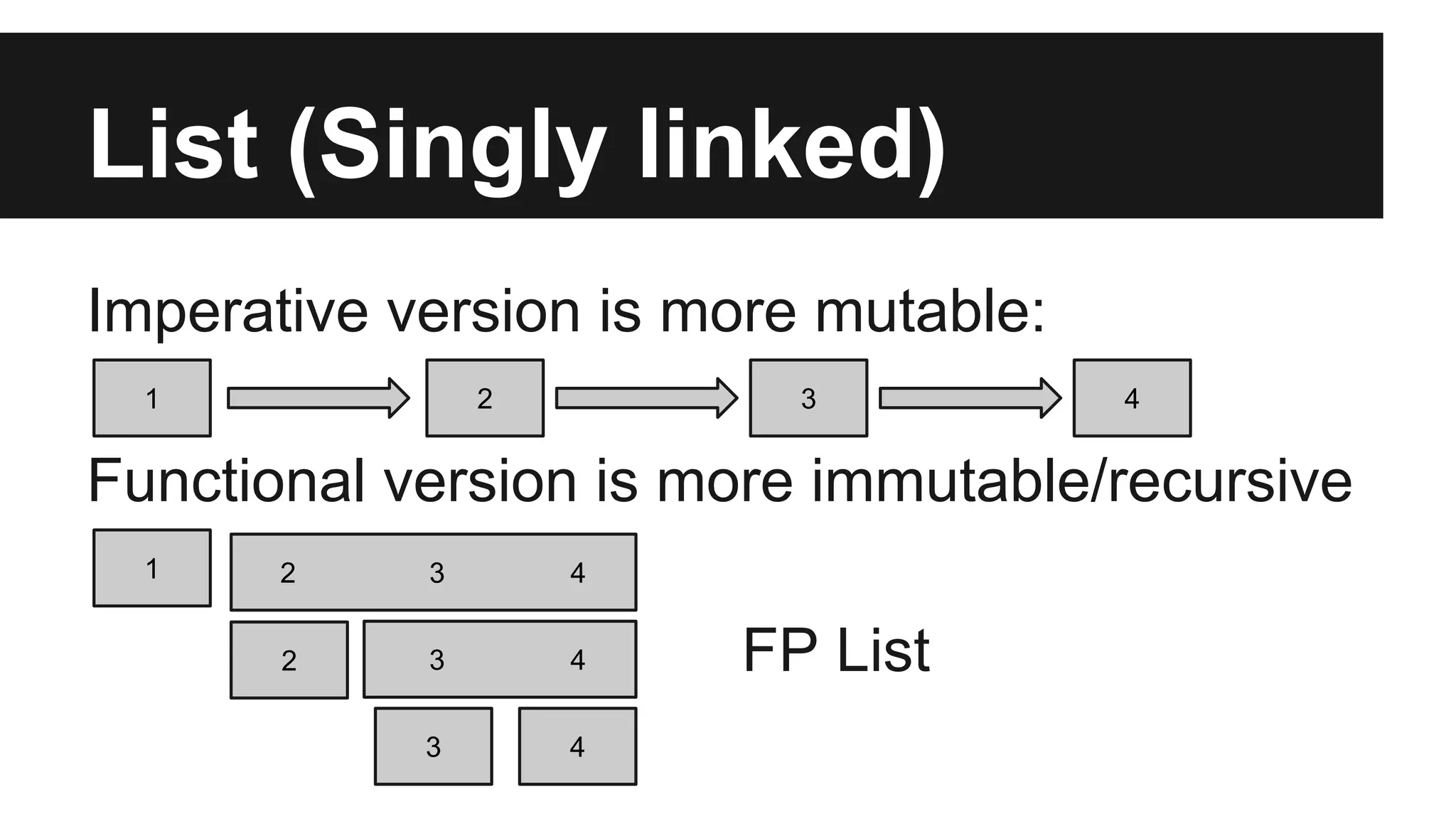
List (Singly linked) Imperative version is more mutable: 1 2 3 4 Functional version is more immutable/recursive FP List 1 2 3 4 2 3 4 3 4

Algebraic Data Type We model List as one Algebraic Data Type In scala ADT are modeled mostly as sealed trait and case classes extends from it. Look at the next slide

pure FP List sealed trait List[+A] case object Nil extends List[Nothing] case class Cons[+A] (head: A, tail: List[A]) extends List[A] object List { def apply[A](as: A*): List[A] = if (as.isEmpty) Nil else Cons(as.head, apply(as.tail: _*)) private def asString_internal[A](l: List[A]): String = l match { case Nil => "" case Cons(head,tail) => head.toString + " " + asString_internal(tail) } def toString[A](l: List[A]): String = "[ " + asString_internal(l) + "]" }

traits traits in scala is similar to mixins in Ruby It is contains certain functionality/interface that can be inherited and used by classes, can have both concrete methods and abstract methods. sealed traits means all the class inherit this trait must be in the same file trait in. This give compiler the power to know the “full” set of classes inherit the trait.

case class case class is the special class can be used in functional programming pattern matching mechanism. sealed traits and case class are the standard way in scala to model Algebraic Data Type, which will be the fundamental building blocks of functional programming

companion object object in scala is basically singleton object in other language. You can have a companion object with same name of the class/trait in scala, companion object can have access of the private method/data of the class/trait it associated to. Here we mostly use it as a module for the ADT.

List ADT sealed trait List[+A] case object Nil extends List[Nothing] case class Cons[+A] (head: A, tail: List[A]) extends List[A] Here we define List as a trait, and 2 type of lists are defined, Nil as empty List, and Cons as non-empty List.

Type Variance sealed trait List[+A] A is just abstract type (generic) +A here is called covariant, means that if A` is A’s subtype, then List[A`] is List[A]’s subtype.

Constructor object List { def apply[A](as: A*): List[A] = if (as.isEmpty) Nil else Cons(as.head, apply(as.tail: _*)) … You can create constructor for the List trait with different signatures here, you can have multiple constructor here in companion object.

Pattern Matching private def asString_internal[A](l: List[A]): String = l match { case Nil => "" case Cons(head,tail) => head.toString + " " + asString_internal(tail) } def toString[A](l: List[A]): String = "[ " + asString_internal(l) + "]" } Now we define toString function here, we here use pattern matching to see what is the remaining list type between Nil and Cons. Pattern Matching is a very powerful feature in FP, and it can match into the multiple layers of objects, match types and much more.

Recursive You can also notice that we use recursive here, recursive is preferred in FP to loops. And will avoid mutables. In scala as it is based on Java ByteCode, it is still possible to stack overflow, so we sometime will need to try to do tail recursion as much as possible, we will talk about it later.

Scala is not Pure FP As we can see in early slide, we now have a minimum functional List, it does not really use OO concepts (trait and case class here only use to model ADT). This is kind of pure FP way to do the function programming: A few types and functions that work on the types. If you look at scala doc for their List, it kind of different and toString is directly a method of List. It is in fact more OO/FP hybride way to do it. Let change to that and see.

OO/FP List sealed trait List[+A] { def head: A def tail: List[A] def isEmpty: Boolean override def toString = "[ " + asString_internal(this) + "]" private def asString_internal[B >: A](l: List[B]): String = l match { case Cons(head,tail) => head.toString + " " + asString_internal(tail) case _ => "" } } object List { def apply[A](as: A*): List[A] = if (as.isEmpty) Nil else Cons(as.head, apply(as.tail: _*)) } case object Nil extends List[Nothing] { override def isEmpty = true override def head: Nothing = throw new NoSuchElementException("head of empty list") override def tail: List[Nothing] = throw new UnsupportedOperationException("tail of empty list") } case class Cons[+A] (hd: A, tl: List[A]) extends List[A] { override def isEmpty = false override def head : A = hd override def tail : List[A] = tl }

lower bound (Type variation) asString_internal[B >: A](l: List[B]): String Here the B >: A is called lower bound in type variation, which means that, B must be a supertype of A. This is required to satisfy the type variance check (you can not use A here directly in place of B) check this

More List functions def sum(ints: List[Int]): Int = ints match { case Nil => 0 case Cons(x,xs) => x + sum(xs) } def product(ds: List[Double]): Double = ds match { case Nil => 1.0 case Cons(0.0, _) => 0.0 case Cons(x,xs) => x * product(xs) } These 2 common functions seems really similar, how we can generalize it.

foldRight def foldRight[A,B](l: List[A], z: B)(f: (A, B) => B): B = l match { case Nil => z case Cons(x, xs) => f(x, foldRight(xs, z)(f)) } def sum(l: List[Int]) = foldRight(l, 0)((x,y) => x + y) def product(l: List[Double]) = foldRight(l, 1.0)(_ * _) Here is the higher order function (function take function as parameter or output), a very power/interesting feature in FP. Here _ * _ means the first parameter * second parameter, which is a short hand way to write it.

tail recursion foldRight is abstract and powerful, but it can stack overflow, what can we do? @annotation.tailrec def foldLeft[A,B](l: List[A], z: B)(f: (B, A) => B): B = l match { case Nil => z case Cons(h,t) => foldLeft(t, f(z,h))(f) } def reverse[A](l: List[A]): List[A] = foldLeft(l, List[A]())((acc,h) => Cons(h,acc)) def foldRight[A,B](l: List[A], z: B)(f: (A,B) => B): B = foldLeft(reverse(l), z)((b,a) => f(a,b)) foldLeft is tail recursive, and it enforced (by the annotation) to optimize into loop in background, then we can use this FoldLeft to implement FoldRight (now no stack overflow

map You should be familiar with map on List def map[A, B](la: List[A])(f: A => B): List[B] = foldRight(la, Nil:List[B])((h,t) => Cons(f(h), t)) val a = List(1,2,3,4) List.map(a)(_+1) we get List(2,3,4,5)

There are far more than map def unit[A](a: A): List[A] = Cons(a, Nil) def flatMap[A, B](la: List[A])(f: A => List[B]): List[B] = concat(foldRight(la, Nil:List[List[B]])((h,t) => Cons(f(h),t))) def join[A](lla: List[List[A]]): List[A] = flatMap(lla)(la => la) def compose[A,B,C](f: A => List[B], g: B => List[C]): A => List[C] = a => flatMap(f(a))(g) def apply[A,B](la: List[A])(f: List[A => B]): List[B] = flatMap(f)(t1 => flatMap(la)(t2 => unit(t1(t2)))) def map2[A,B,C](la: List[A], lb: List[B])(f: (A, B) => C): List[C] = apply(lb)(apply(la)(unit(f.curried))) def map[A, B](la: List[A])(f: A => B): List[B] = apply(la)(unit(f)) def fold[A](l: List[A])(z: A)(op: (A, A) ⇒ A): A = foldRight(l, z)(op) def filter[A](l: List[A])(f: A => Boolean): List[A] = foldRight(l, Nil:List[A])((h,t) => if (f(h)) Cons(h,t) else t)

What are they You can see, except for unit[A](a: A): List[A] fold[A](l: List[A])(z: A)(op: (A, A) ⇒ A): A filter[A](l: List[A])(f: A => Boolean): List[A] There are 3 groups: 1. flatMap/join/compose 2. apply/map2 3. map inside each group, the methods are equivalent to each other. G1 => G2 => G3, which means G1 can implement G2, G2 can implement G3. Powerful G1 > G2 > G3 Generality G1 < G2 < G3 OO sense, G1 inherit from G2 inherit from G3

What are they G1 is Monad Signature G2 is Applicative Signature G3 is Functor Signature fold is the signature of Foldable Monad with filter is called Zero Monad It is easier to see, but much harder to understand. What they are. Why we use them. What can they do. Once you understand, you lost the ability to say it :) We will find out that through our journey. Here we can have a small taste first.

Scala for comprehension Any type that has flatMap/map/filter defined on them can use for comprehension. Let us put those in OO/FP hybrid style

for comprehension Use the OO/FP hybrid style code we can do def test = { val a = List(1,2) val b = List(3,4) for { t1 <- a t2 <- b } yield ((t1,t2)) } We get [ (1,3) (1,4) (2,3) (2,4) ]

for comprehension It is in fact flatMap/map in disguise, it is same as def test = { val a = List(1,2) val b = List(3,4) a.flatMap { t1 => b.map { t2 => (t1,t2) } } } basically multiple List can combine together in any ways, without knowing what inside, the last one is map, all the other are flatMap, you can also use if here in for comprehension, which translate into filter

Fp in scala part 1

More Related Content

What's hot

Similar to Fp in scala part 1

Recently uploaded

Fp in scala part 1