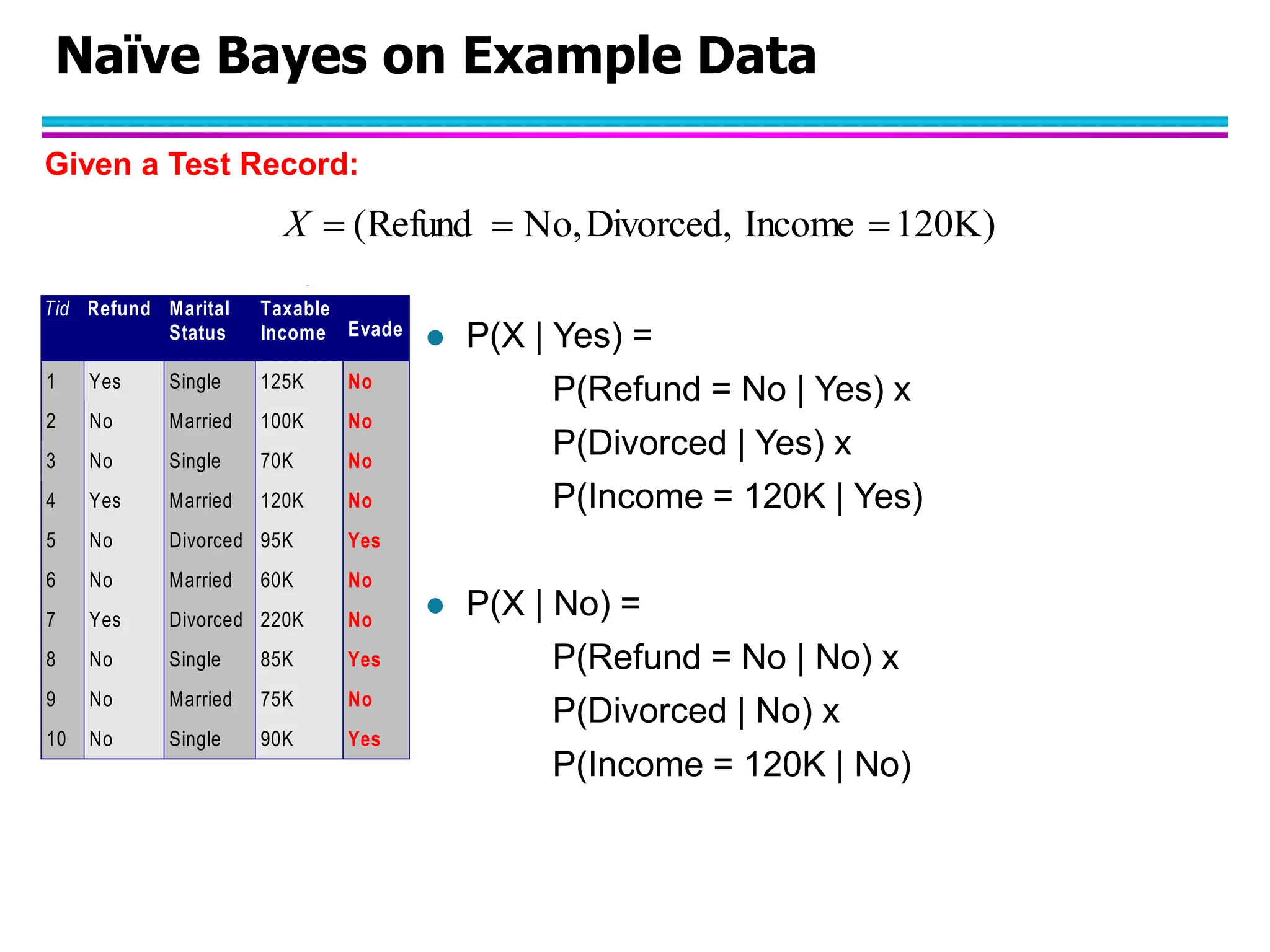
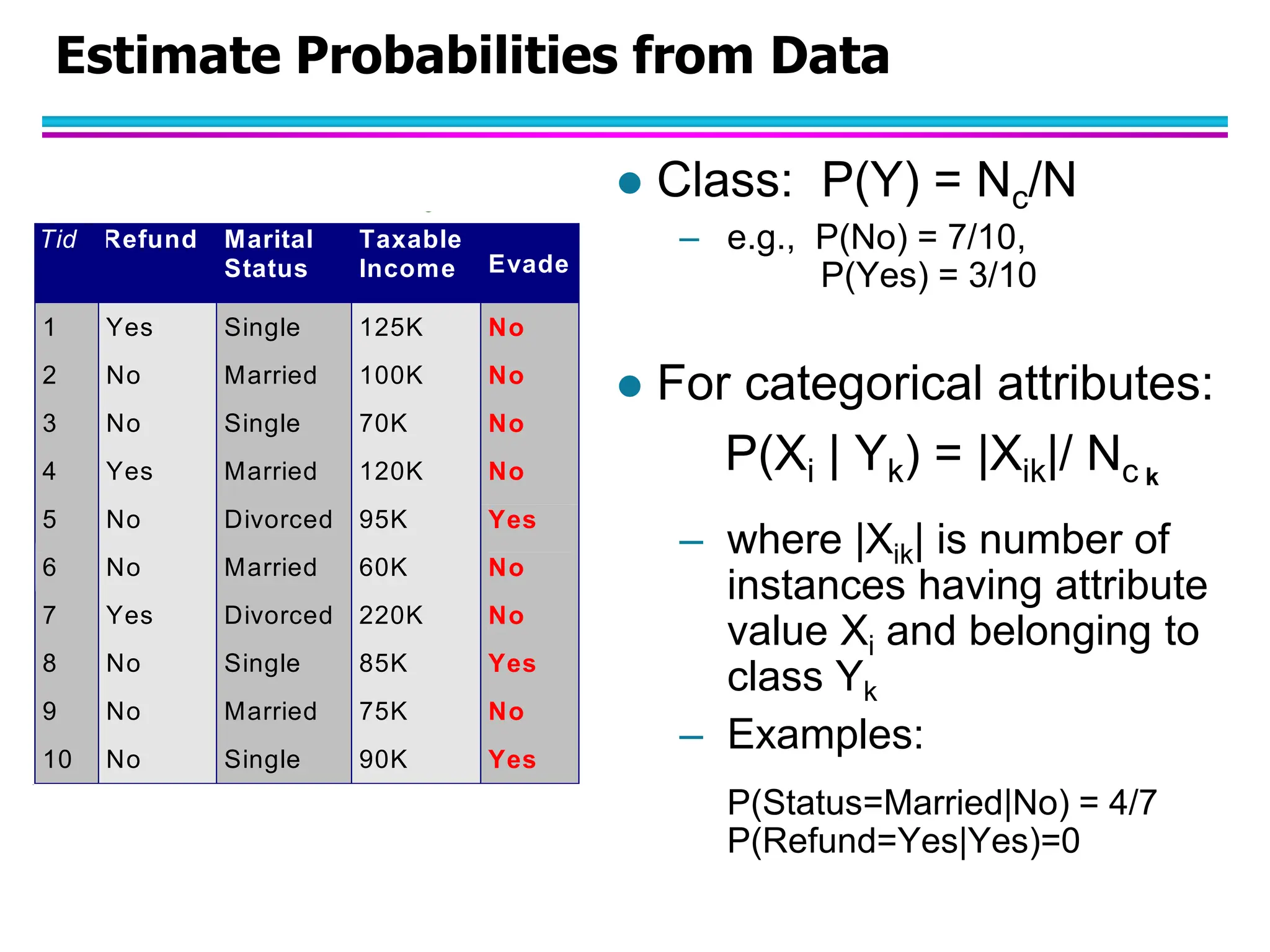
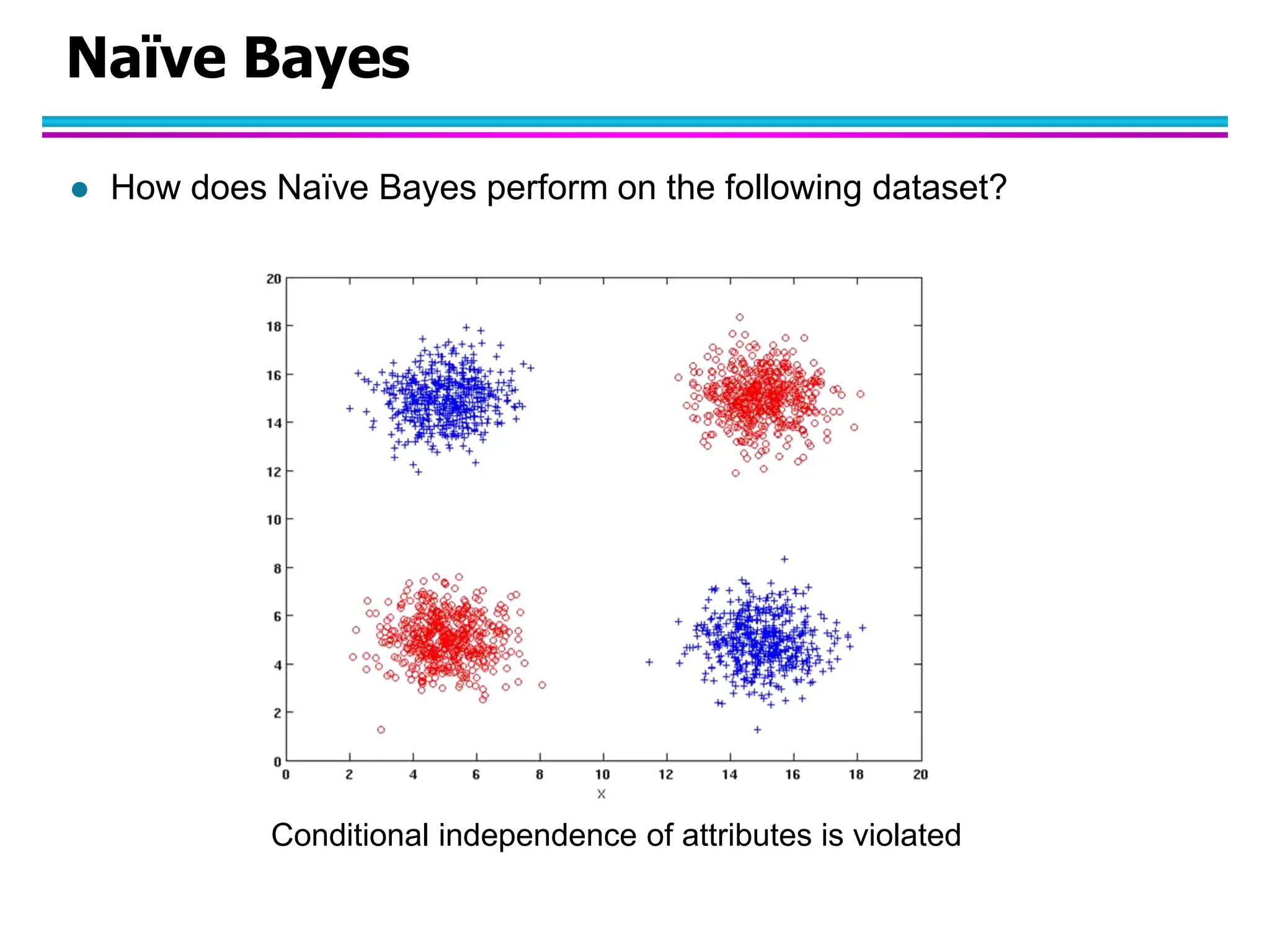
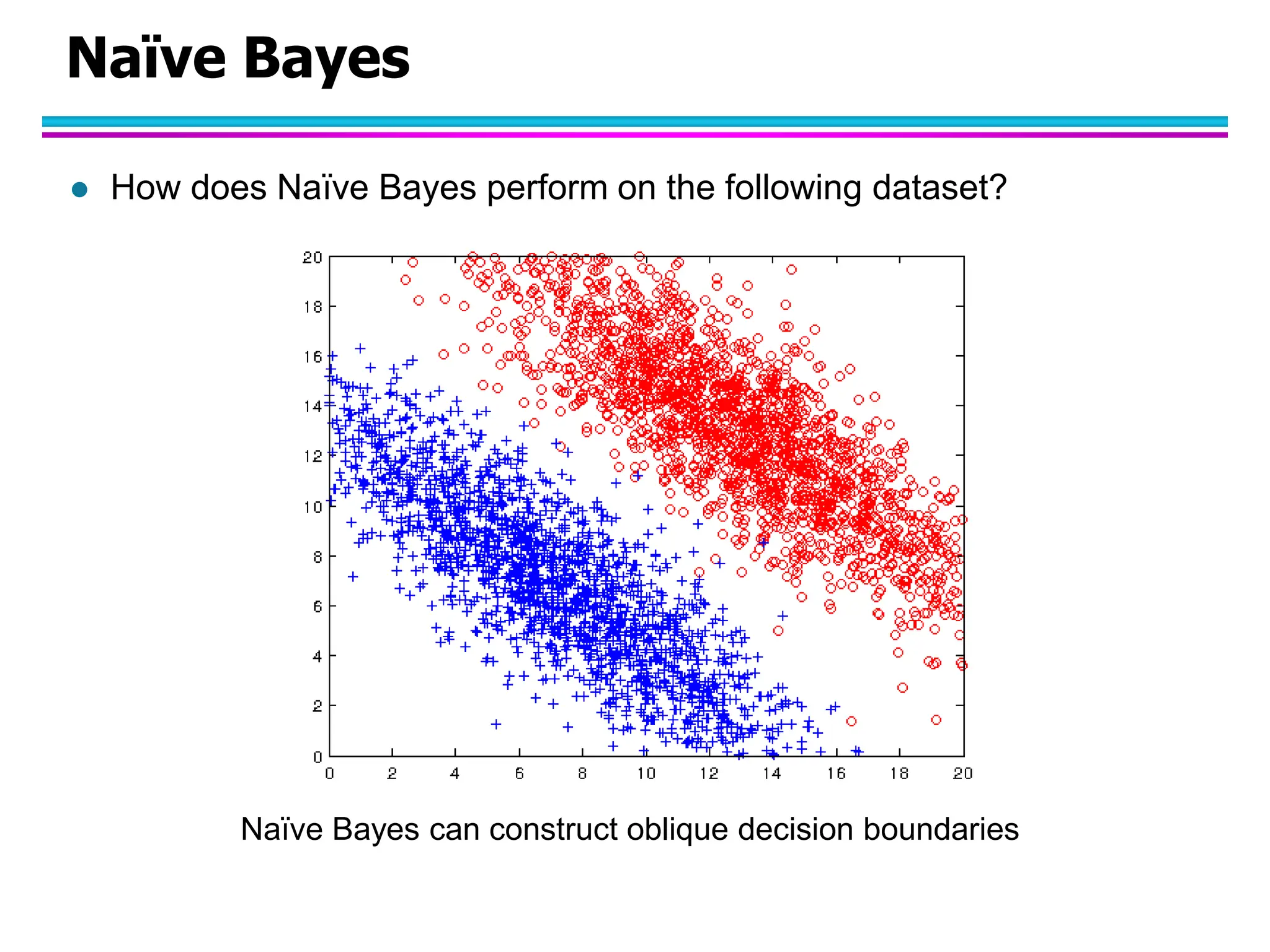
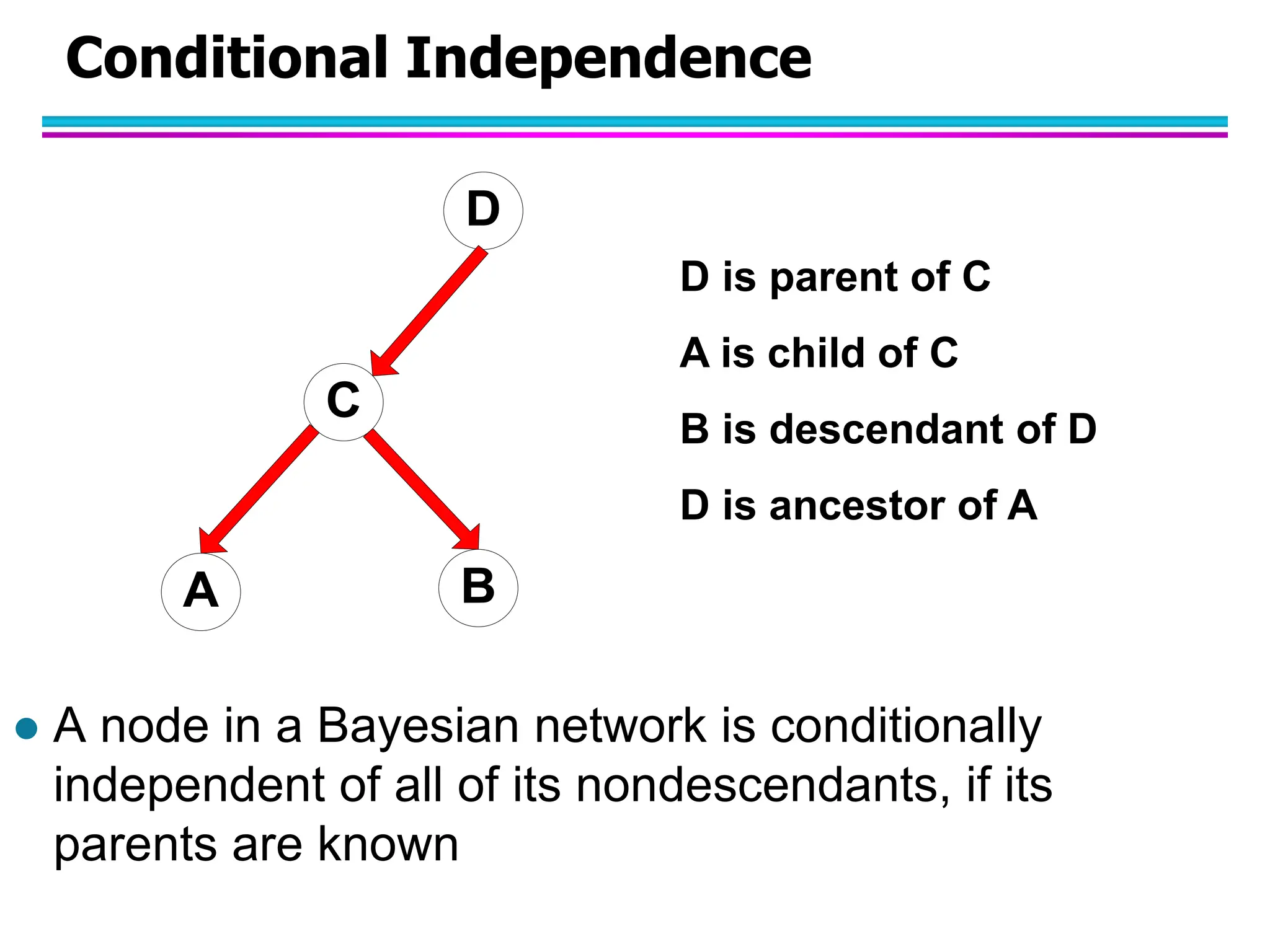
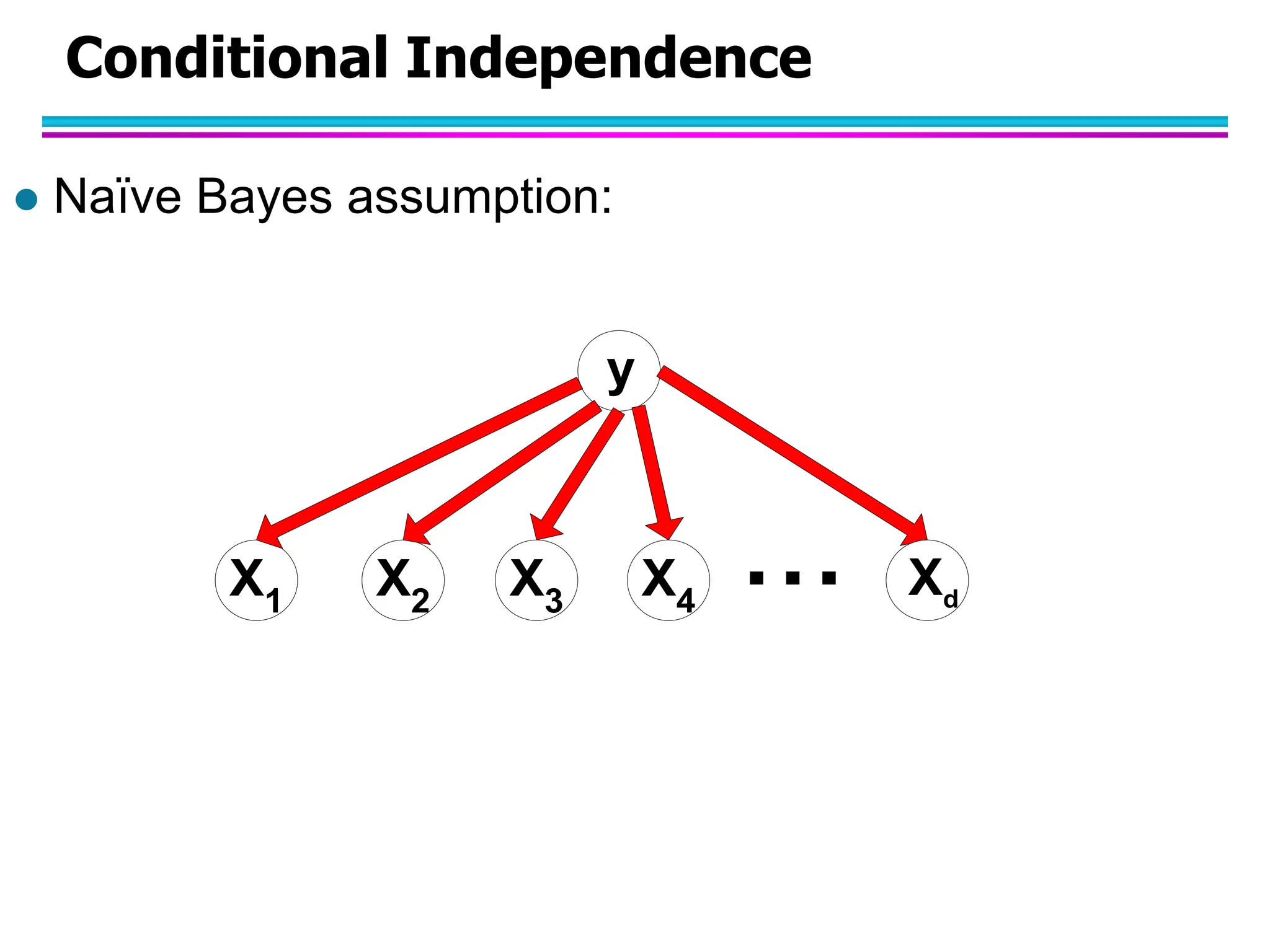
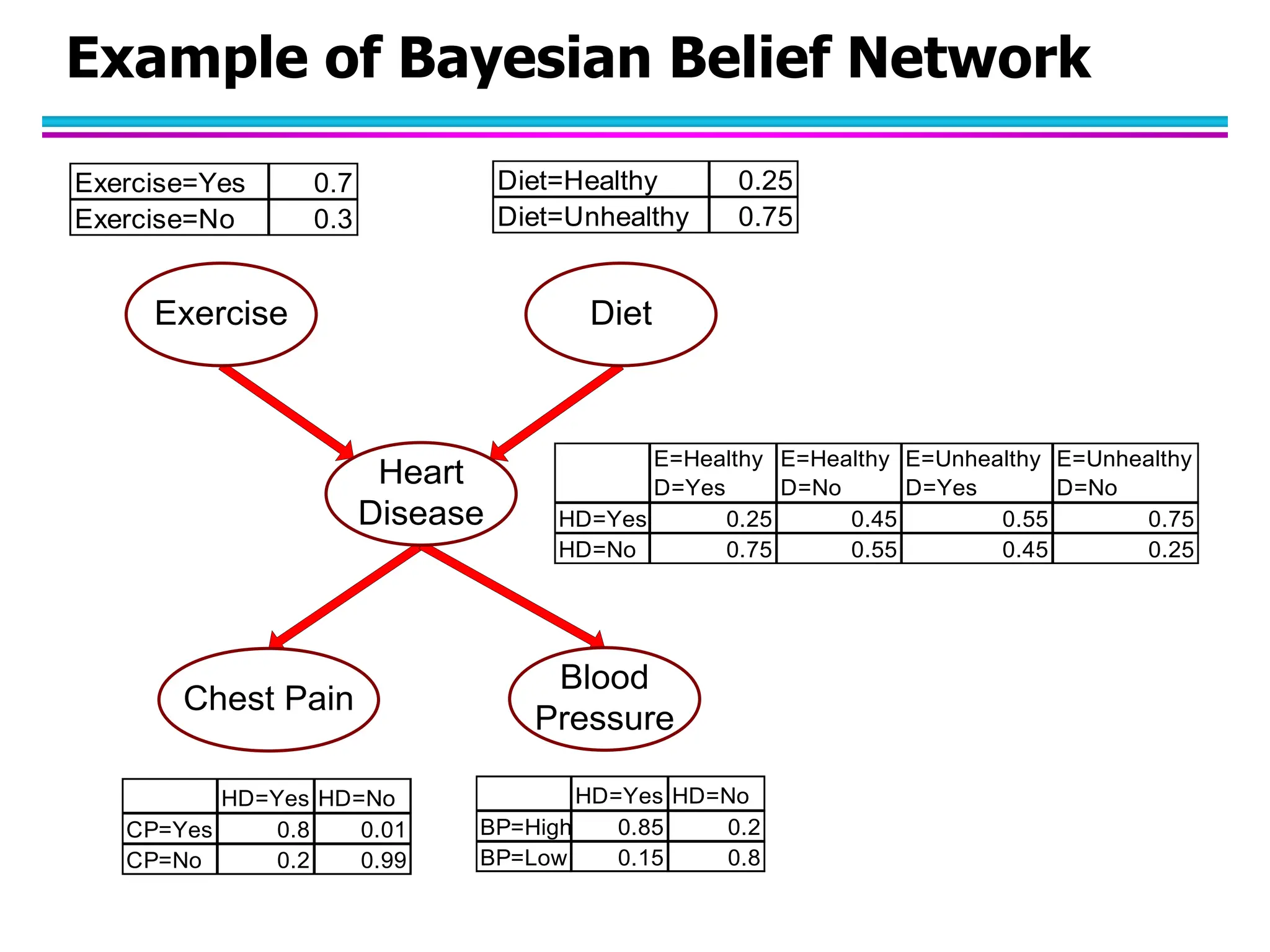
The document discusses Bayesian classifiers, particularly focusing on Naive Bayes classifiers and their application in data mining for classification tasks. It explains Bayes' theorem, how to calculate probabilities for classification, and common issues such as handling zero probabilities in training data. The document also highlights the robustness of Naive Bayes against noise and irrelevant attributes, while addressing its limitations regarding the independence assumption among attributes.