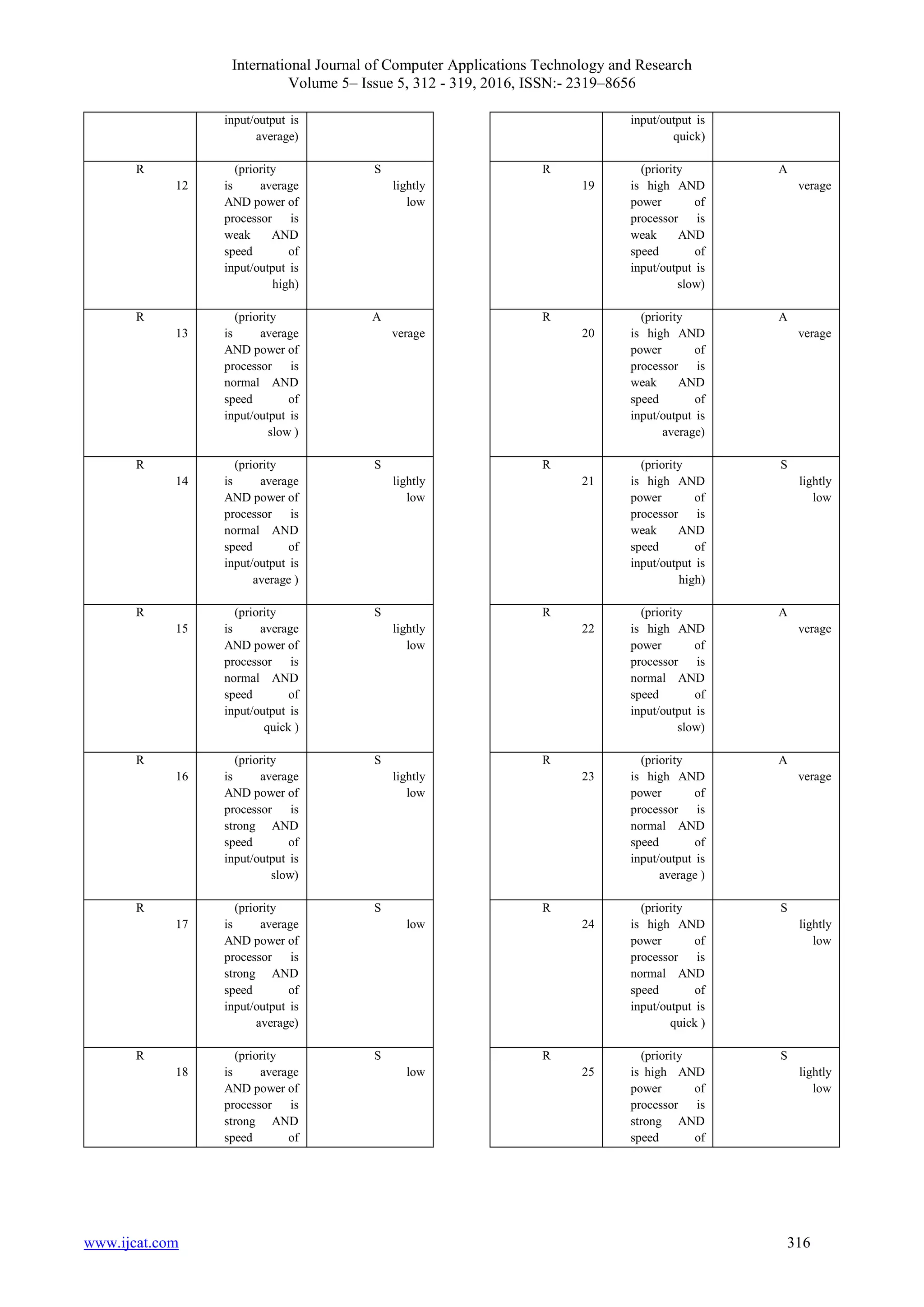
The document presents a novel algorithm for task scheduling in grid computing based on a Mamdani fuzzy system, aiming to improve efficiency by utilizing fuzzy models to measure response times. It outlines the three stages of task scheduling: resource detection, information collection, and task execution, while comparing its performance against existing algorithms. The proposed method shows significant improvements in criteria for scheduling algorithms, such as completion and waiting times.



![International Journal of Computer Applications Technology and Research Volume 5– Issue 5, 312 - 319, 2016, ISSN:- 2319–8656 www.ijcat.com 315 In the second stage, rules database is created. Generally, it can be said that, in fuzzy inference stage, linguistic variables are executed on the basis of input linguistic variables, system rules and membership function, (fuzzy values). In Mamdani method, the methods of “multiplication-maximum” and “minimum- maximum” are used. In our proposed method, “maximum- minimum” method is used for fuzzy inference. The formula used for this purpose is as follows. 𝑶𝑹 = 𝝁 𝑶𝑹 𝑨𝑩(𝒙) = 𝐦𝐚𝐱[𝝁𝑨(𝒙), 𝝁𝑩(𝒙)] 𝑨𝑵𝑫 = 𝝁 𝑨𝑵𝑫 𝑨𝑩(𝒙) = 𝐦𝐢𝐧[𝝁𝑨(𝒙), 𝝁𝑩(𝒙)] After identifying formula, we follow fuzzy rules of knowledge base. According to input criteria and linguistic variables, rules of knowledge base are defined as follows. Table 1. The rules of knowledge base of Mamdani fuzzy system Response Time C on dition R ule H igh t hen (priority is low AND power of processor is weak AND speed of input/output is slow) R 1 if H igh (prio rity is low AND power of processor is weak AND speed of input/output is average) R 2 S lightly high (priority is low AND power of processor is weak AND speed of input/output is high) R 3 S lightly high (priority is low AND power of processor is normal AND speed of R 4 input/output is slow ) S lightly high (priority is low AND power of processor is normal AND speed of input/output is average ) R 5 A verage (priority is low AND power of processor is normal AND speed of input/output is quick ) R 6 A verage (priority is low AND power of processor is strong AND speed of input/output is slow) R 7 A verage (priority is low AND power of processor is strong AND speed of input/output is average) R 8 A verage (priority is low AND power of processor is strong AND speed of input/output is quick) R 9 A verage (priority is average AND power of processor is weak AND speed of input/output is slow) R 10 A verage (priority is average AND power of processor is weak AND speed of R 11](https://image.slidesharecdn.com/ijcatr05051013-160703091943/75/Presenting-an-Algorithm-for-Tasks-Scheduling-in-Grid-Environment-along-with-Increasing-Efficiency-by-using-Fuzzy-Models-4-2048.jpg)
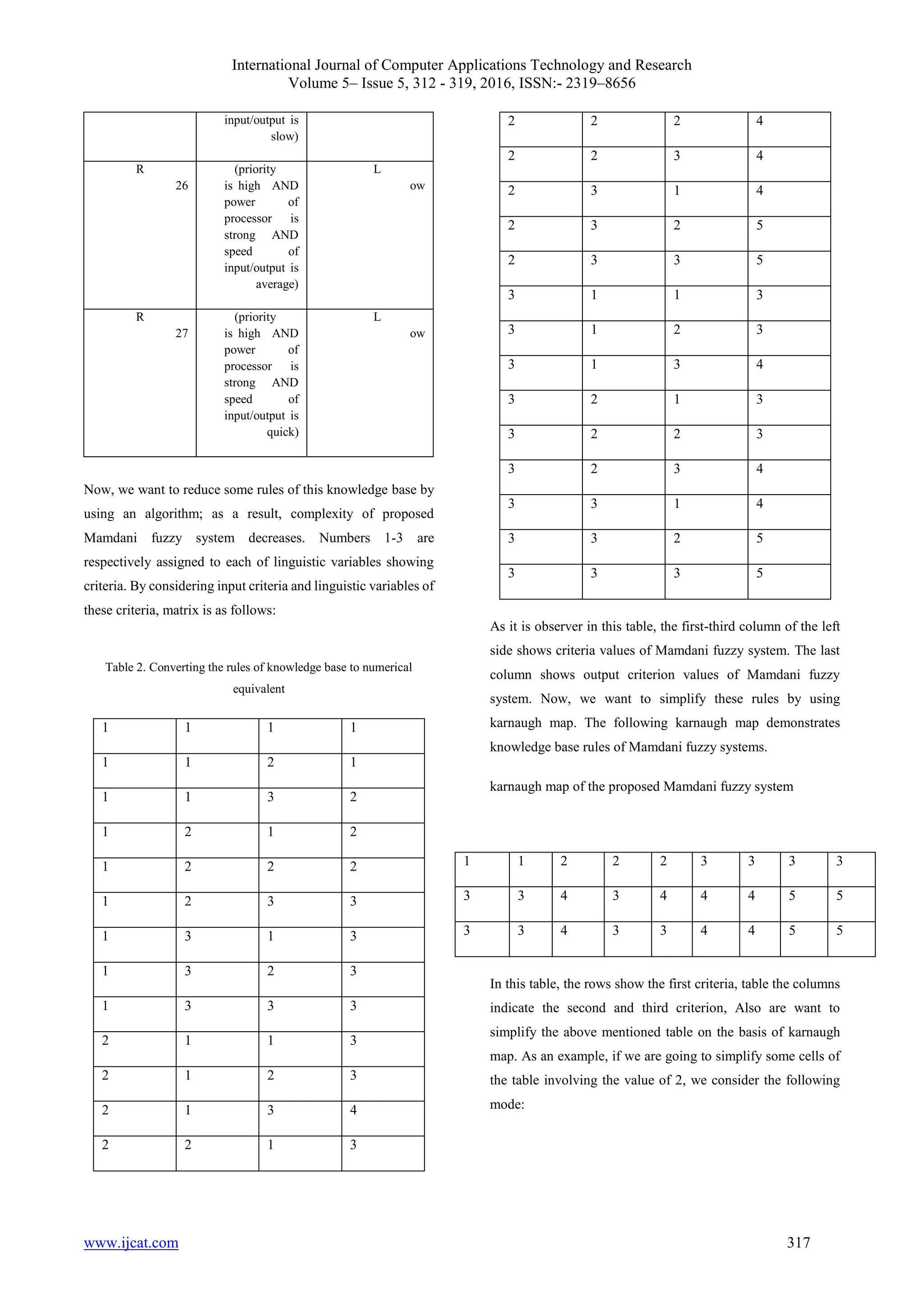
![International Journal of Computer Applications Technology and Research Volume 5– Issue 5, 312 - 319, 2016, ISSN:- 2319–8656 www.ijcat.com 318 Table 3. Classification of karnaugh map with numerical values of 2 1 1 2 2 2 3 3 3 3 3 3 4 3 4 4 4 5 5 3 3 4 3 3 4 4 5 5 =1)OR3=2)] AND [(x2=1) OR(x2=1) AND [(x1If((x =2final=3)]) THEN X3(x=2)OR3(x In this rule, X1-X3 shows input criteria, and Xfinal demonstrated output parameter. Table 4. The rules of knowledge base after simplification Rule Condition Response Time Rule R1 If((x1=1)AND (x2=1)AND(x3=1 OR 2)) HIGH R1 R2 If((x1=1) AND [(x2=1) OR(x2=2)] AND [(x3=1)OR (x3=2)OR (x3=3)]) THEN SLOWLY HIGH R2 According to the rules obtained from above table, it is observed that the rules reduce from 27 to 11 rules, and in this case, complexity of Mamdani system decreases. For example, we consider the action of and as 8 units, then we have: For 27 rules: Execution time 27*2*2=108 For 11 rules: Execution time=22*2+21*1=65 3.3 Case Study Now, we want to implement our proposed algorithm on a system, and measure reliability and response time in the mentioned methods. In case studies, we try to find small and comprehensive examples. In this case, there isn't any complexity, and it is a small sample of other big and real examples. The example of bank ATM lacks much complexity, and it involves architecture products. In this example, appropriate architecture frame of CαISR has been taken into account. We compute reliability and response time by using the proposed method and executable model simulation. 3.4 Implementation The following table shows the values of input criteria in the proposed system for processes. Table 5. The values of each input parameters ATM system S.I/OP.O.PA.PET 43118 9732 2221 5964 3653 781112 81713 ET is execution time of the process, A.P is real priority of the process, P.O.P refers to the processor's power and S.I/O points to execution speed of input and output operations. Also, it is supposed that all processes enter the system in zero time. After entering required parameters of proposed Mamdani system, we should determine the priority of processes for execution by using the mentioned membership function of the algorithm. The following table shows this procedure as well as possible. Table 6. converting each value of input parameters to fuzzy equivalents Linguistic variable for new priority μnewμpμb Low0.0830.08330.0528 High0.8950.250.8948 High0.950.1660.9474 High0.790.50.7895 High0.840.41660.8422 High0.9170.91660.3685 Average0.580.58330.3158 After obtaining a new priority for processes, execution procedure of these processes is as follows: P3,P6,P2,P5,P4,P7,P1 After identifying execution procedure of processes, the response time is as follows. Waiting time= 14.86 Response time= 33 After determining input parameters positions, we follow the heart of Mamdani system called inference system of knowledge base. After implementing Mamdani system in CPN, we use MATLAB to obtain output results and to display output membership functions by using input membership functions. X1 X2X3](https://image.slidesharecdn.com/ijcatr05051013-160703091943/75/Presenting-an-Algorithm-for-Tasks-Scheduling-in-Grid-Environment-along-with-Increasing-Efficiency-by-using-Fuzzy-Models-7-2048.jpg)
![International Journal of Computer Applications Technology and Research Volume 5– Issue 5, 312 - 319, 2016, ISSN:- 2319–8656 www.ijcat.com 319 Figure 5. Obtained diagram for response time by implementing the system on MATLAB As it can be observed in the figure, we can measure response time of ATM system by using simple Mamdani fuzzy system. 4. CONCLUSION Computing grids provide inexpensive and reliable accessing to others, computing resources. These recourses are heterogeneous, and they are distributed. Also, they are commonly used. On the other side, resources in grid belong to different organizations having managerial policies, models and costs for various users in different time. In this way, owners and users of resources have different objectives, strategies and different supply and demands. In order to manage such a complex environment, common methods trying to optimize efficiency in system level cannot be used to manage the resources. In this thesis, a new method has been presented to schedule tasks in computing grid environment. In this method applied on the basis of Mamdani fuzzy system, execution time parameter is considered to improve efficiency and performance. In this algorithm, parameters required to evaluate the response time are firstly calculated by using membership functions in Mamdani fuzzy system. Then, the criterion of response time is measured for Mamdani fuzzy system by using output MATLAB software. The results indicate priority of the proposed algorithm in comparison with other previous algorithms. 5. SUGGESTIONS One of the ideas stated about heuristic algorithm is to study and present new scheduling methods combining other parameters like reliability, load balance and etc and obtaining interesting results. In terms of using Mamdani fuzzy system algorithm, it can be proposed that this algorithm is used in combination with other algorithms. Another suggestion is using some mechanisms for applications classification and dividing the problems to subtasks. If we can do this task by a mechanism with high precision and speed and by considering tasks duration as a determinant of load balance in distributed systems especially grid system, then scheduling precision and speed will be high. In this case, resources are appropriately dedicated, and efficiency and performance increases in grid system. Future suggestions a terms of scheduling in grid environment are as follows: 1) Studying the methods of error tolerance in proposed algorithms 2) Presenting scheduling in hierarchical order 3) Measuring several parameters in Mamdani fuzzy system 6. REFERENCES [1] Afzal, A., McGough, A.S., Darlington, J., "Capacity planning and scheduling in Grid computing environment", Journal of Future Generation Computer Systems 24 , pp 404-414, 2008. [2] BenDaly Hlaoui Y., Jemni BenAyed L.; "Toward anUML-based Composition of Grid Services Workflows",Research Unit of Technologies of Information and Communication, Tunisia, ACM,AUPC’08, July 2008. [3] . Dai, Y.S., Levitin, G., "Optimal Resource Allocation for Maximizing Performance and Reliability in Tree- Structured Grid Services", IEEE Transaction on Reliability, Vol. 56, No.3, September 2007. [4] Dai, Y.S., Xie, M., Poh, K.l., "Reliability of grid service systems", Computers & Industrial Engineering 50, pp.130-147, Elsevier, 2006. [5] Foster, I., Kesselman, C., The Grid 2: Blueprint for a New Computing Infrastructure, Los Alios, Morgan- Kuffman,2003. [6] G. Murugesan1, An Economic-based Resource Management and Scheduling for Grid Computing Applications, IJCSI International Journal of Computer Science Issues, Vol. 7, Issue 2, No 5, March 2010 [7] Kordic V., Petri Net Theory and Applications, Chapter:Model Checking of Time Petri Nets, Chapter Author:Boucheneb H., Hadjidj R., I-Tech Education and Publishing, Vienna, Austria, First Edition, February 2008. [8] Levitin, G., Dai, Y.S., "Service reliability and performance in grid system with star topology", Reliability Engineering and System Safety 92, pp. 40-46, Elsevier, 2007. [9] Li, M., Baker, M., The Grid Core Technologies, John Wiley & Sons Publishing, 2005 [10] Yagoubi, B., Slinani, Y., "Task Load Balancing Strategy for Grid Computing", Journal of Computer Science 3 (3),pp. 186-194, 2007 [11] Saeed Parsa. Fereshteh- Azadi Parand. 2012.Estimation of service reliability and performance in gr id environment: Journal of King Saud Univer sity Engineer ing Sciences vol: 24,pp: 151 157.. Cihan H. Dagli. 2011. Modified SPEA2 for Probabilistic Reliability Assessment: Procedia Computer Science volume 6 ,pp: 435 44.](https://image.slidesharecdn.com/ijcatr05051013-160703091943/75/Presenting-an-Algorithm-for-Tasks-Scheduling-in-Grid-Environment-along-with-Increasing-Efficiency-by-using-Fuzzy-Models-8-2048.jpg)