Quality Python Homework Help

For any help regarding Python Homework Help visit : - https://www.pythonhomeworkhelp.com/, Email :- support@pythonhomeworkhelp.com or call us at :- +1 678 648 4277

1 Difference Equations System 1: Consider the system represented by the following difference equation where x th [n] and y[n] represent the n samples of the input and output signals, respectively 1.1 Poles Determine the pole(s) of this system. number of poles: 2 list of pole(s): 3 and −1/2 1.2 Behavior Does the unit-sample response of the system converge or diverge as n → ∞? converge or diverge: diverge

Briefly explain. System 2: Consider a different system that can be described by a difference equation of the form y[n] = x[n] + Ay[n − 1] + By[n − 2] where A and B are real-valued constants. The system is known to have two poles, given by 1/2 ±j 1/3 . 1.3 Coefficients Determine A and B. A = 1 B = -13/36 1.4 Behavior Does the unit-sample response of the system converge or diverge as n → ∞?

converge or diverge: converge Briefly explain. 2 Geometry OOPs We will develop some classes and methods to represent polygons. They will build on the following class for representing points. class Point: def __init__(self, x, y): self.x = x self.y = y

def distanceTo(self, p): return math.sqrt((self.x - p.x)**2 + (self.y - p.y)**2) def __str__(self): return ’Point’+str((self.x, self.y)) __repr__ = __str__ 2.1 Polygon class Define a class for a Polygon, which is defined by a list of Point instances (its vertices). You should define the following methods: • __init__: takes a list of the points of the polygon, in a counter-clockwise order around the polygon, as input • perimeter: takes no arguments and returns the perimeter of the polygon >>> p = Polygon([Point(0,0),Point(1,0),Point(1,1),Point(0,1)]) >>> p.perimeter() 4.0

class Polygon: def __init__(self, p): self.points = p def perimeter(self): p = self.points n = len(p) per = 0 for i in range(n): per += p[i].distanceTo(p[(i+1)%n]) return per 2.2 Rectangles Define a Rectangle class, which is a subclass of the Polygon class, for an axis-aligned rectangle which is defined by a center point, a width (measured along x axis), and a height (measured along y axis). >>> s = Rectangle(Point(0.5, 1.0), 1, 2) This has a result that is equivalent to >>> s = Polygon([Point(0, 0), Point(1, 0), Point(1, 2), Point(0, 2)])

Define the Rectangle class; write as little new code as possible. class Rectangle(Polygon): def __init__(self, pc, w, h): points = [Point(pc.x - w/2.0, pc.y - h/2.0), Point (pc.x + w/2.0, pc.y - h/2.0), Point(pc.x + w/2.0, pc.y + h/2.0), Point(pc.x - w/2.0, pc.y + h/2.0)] Polygon.__init__(self, points) 2.3 Edges Computing the perimeter, and other algorithms, can be conveniently organized by iterating over the edges of a polygon. So, we can describe the polygon in terms of edges, as defined in the following class: class Edge: def __init__(self, p1, p2): self.p1 = p1 self.p2 = p2 def length(self): return self.p1.distanceTo(self.p2)

def determinant(self): return self.p1.x * self.p2.y - self.p1.y * self.p2.x def __str__(self): return ’Edge’+str((self.p1, self.p2)) __repr__ = __str__ Assume that the __init__ method for the Polygon class initializes the attribute edges to be a list of Edge instances for the polygon, as well as initializing the points. Define a new method, sumForEdges, forthe Polygon class that takes a procedure as an argument, which applies the procedure to each edge and returns the sum of the results. The example below simply returns the number of edges in the polygon. >>> p = Polygon([Point(0,0),Point(2,0),Point(2,1),Point(0,1)]) >>> p.sumForEdges(lambda e: 1) def sumForEdges(self, f): return sum([f(e) for e in self.edges])

2.4 Area A very cool algorithm for computing the area of an arbitrary polygon hinges on the fact that: The area of a planar non-self-intersection polygon with vertices (x0, y0), . . . ,(xn, yn) is where |M| denotes the determinant of a matrix, defined in the two by two case as: Note that the determinant method has already been implemented in the Edge class. Use the sumForEdges method and any other methods in the Edge class to implement an area method for the Polygon class. def area(self): return 0.5*self.sumForEdges(Edge.determinant) or def area(self): return 0.5*self.sumForEdges(lambda e: e.determinant())

or def aux(e): return e.determinant() def area(self): return 0.5*self.sumForEdges(aux) 3 Signals and Systems Consider the system described by the following difference equation: y[n] = x[n] + y[n − 1] + 2y[n − 2] . 3.1 Unit-Step Response Assume that the system starts at rest and that the input x[n] is the unit-step signal u[n].

Find y[4] and enter its value in the box below. y[4] = 21 We can solve the difference equation by iterating, as shown in the following table. n x[n] y[n − 1] y[n − 2] y[n] 0 1 0 0 1 1 1 1 0 2 2 1 2 1 5 3 1 5 2 10 4 1 10 5 21 3.2 Block Diagrams The system that is represented by the following difference equation y[n] = x[n] + y[n − 1] + 2y[n − 2] can also be represented by the block diagram below (left).

It is possible to choose coefficients for the block diagram on the right so that the systems represented by the left and right block diagrams are “equivalent”.1 Enter values of p0, p1, A, and B that will make the systems equivalent in the boxes below p0 = 2 A = 2/3 p1 = −1 B = 1/3 For the left diagram, Y = X + RY + 2R2Y so the system function is For the right diagram,

The two systems are equivalent if Equating denominators, p0p1 = −2 and p0 + p1 = 1, i.e., p0 = 2 and p1 = −1. Equating numerators, A + B = 1 and p1A + p0B = 0, i.e., A = 2/3 and B = 1/3. 4 Robot SM In Design Lab 2, we developed a state machine for getting the robot to follow boundaries. Here, we will develop a systematic approach for specifying such state machines. We start by defining a procedure called inpClassifier, which takes an input of type io.SensorInput and classifies it as one of a small number of input types that can then be used to make decisions about what the robot should do next.

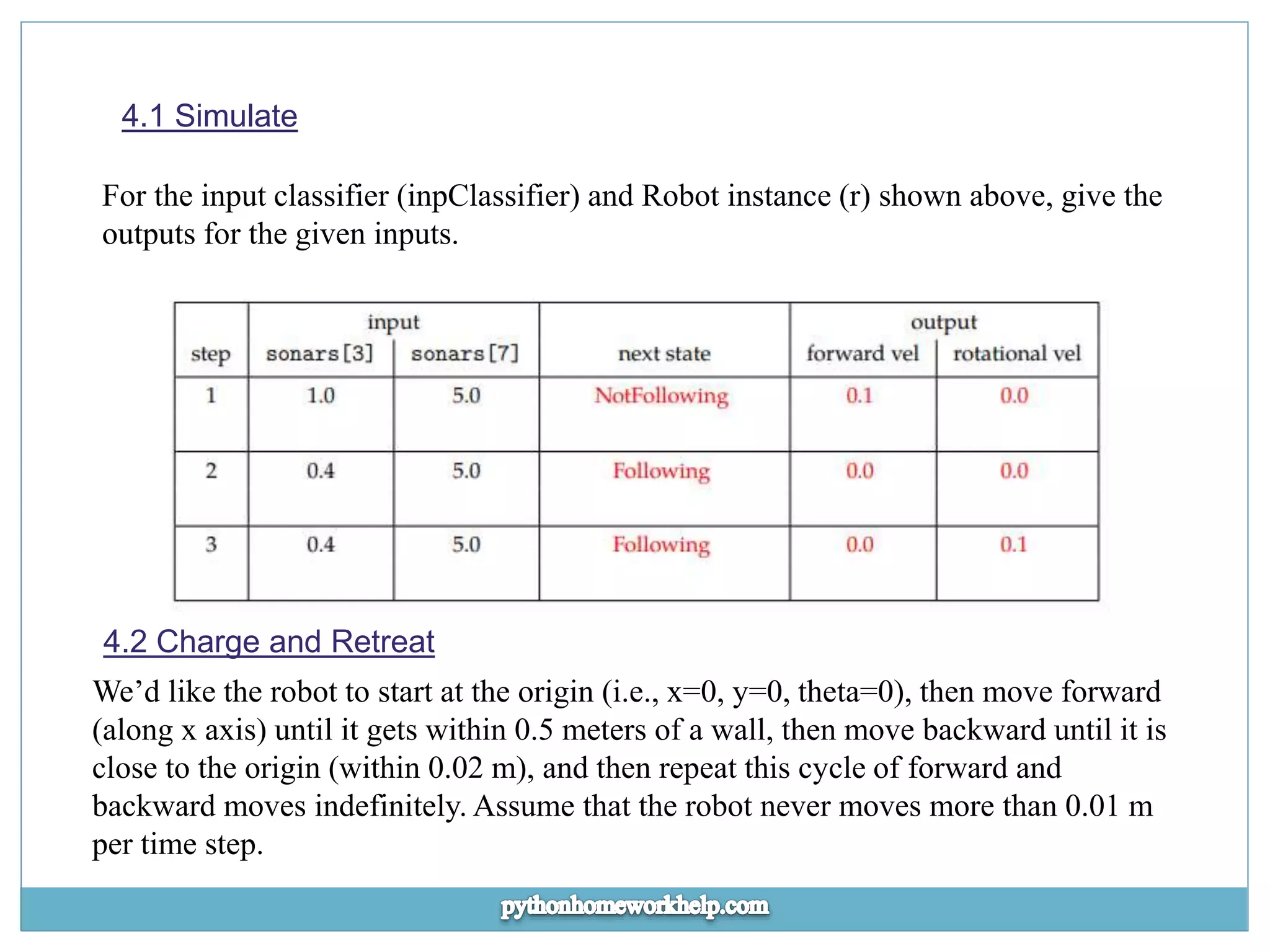
Recall that instances of the class io.SensorInput have two attributes: sonars, which is a list of 8 sonar readings and odometry which is an instance of util.Pose, which has attributes x, y and theta. Here is a simple example: def inpClassifier(inp): if inp.sonars[3] < 0.5: return ’frontWall’ elif inp.sonars[7] < 0.5: return ’rightWall’ else: return ’noWall’ Next, we create a class for defining “rules.” Each rule specifies the next state, forward velocity and rotational velocity that should result when the robot is in a specified current state and receives a particular type of input. Here is the definition of the class Rule: class Rule: def __init__(self, currentState, inpType, nextState, outFvel, outRvel): self.currentState = currentState self.inpType = inpType self.nextState = nextState self.outFvel = outFvel self.outRvel = outRvel

Thus, an instance of a Rule would look like this: Rule(’NotFollowing’, ’frontWall’, ’Following’, 0.0, 0.0) which says that if we are in state ’NotFollowing’ and we get an input of type ’frontWall’, we should transition to state ’Following’ and output zero forward and rotational velocities. Finally, we will specify the new state machine class called Robot, which takes a start state, a list of Rule instances, and a procedure to classify input types. The following statement creates an instance of the Robot class that we can use to control the robot in a Soar brain. r = Robot(’NotFollowing’, [Rule(’NotFollowing’, ’noWall’, ’NotFollowing’, 0.1, 0.0), Rule(’NotFollowing’, ’frontWall’, ’Following’, 0.0, 0.0), Rule(’Following’, ’frontWall’, ’Following’, 0.0, 0.1)], inpClassifier) Assume it is an errorif a combination of state and input type occurs that is not covered in the rules. In that case, the state will not change and the output will be an action with zero velocities.

4.1 Simulate For the input classifier (inpClassifier) and Robot instance (r) shown above, give the outputs for the given inputs. 4.2 Charge and Retreat We’d like the robot to start at the origin (i.e., x=0, y=0, theta=0), then move forward (along x axis) until it gets within 0.5 meters of a wall, then move backward until it is close to the origin (within 0.02 m), and then repeat this cycle of forward and backward moves indefinitely. Assume that the robot never moves more than 0.01 m per time step.

Write an input classifier for this behavior. def chargeAndRetreatClassifier(inp): if inp.sonars[3] < 0.5: return ’frontWall’ el if inp.odometry.x < 0.02: return ’origin’ else: return ’between’ 4.3 Robot instance Write an instance of the Robot class that implements the charge-and-retreat behavior described above. Make sure that you cover all the cases. FB = Robot(’Forward’, [Rule(’Forward’, ’between’, ’Forward’, 0.1, 0), Rule(’Forward’, ’origin’, ’Forward’, 0.1, 0), Rule(’Forward’, ’frontWall’, ’Reverse’, 0.0, 0), Rule(’Reverse’, ’frontWall’, ’Reverse’, -0.1, 0.0), Rule(’Reverse’, ’between’, ’Reverse’, -0.1, 0.0), Rule(’Reverse’, ’origin’, ’Forward’, 0.0, 0.0)], chargeAndRetreatClassifier)

4.4 Matching Write a procedure match(rules, inpType, state) that takes a list of rules, an input type classification, and a state, and returns the rule in rules that matches inpType and state if there is one, and otherwise returns None. def match(rules, inpType, state): for r in rules: if r.inpType == inpType and r.currentState == state: return r return None Complete the definition of the Robot class below; use the match procedure you defined above. Recall that, at each step, the output must be an instance of the io.Action class; to initialize an instance of io.Action, you must provide a forward and a rotational velocity. If a combination of state and input type occurs that is not covered in the rules, remain in the same state and output an action with zero velocity. class Robot(sm.SM): def __init__(self, start, rules, inpClassifier): self.startState = start self.rules = rules self.inpClassifier = inpClassifier

def getNextValues(self, state, inp): inpType = self.inpClassifier(inp) r = match(self.rules, inpType, state) if r: return (r.nextState, io.Action(r.outFvel, r.outRvel) else: return (state, io.Action(0, 0)) 5 Feedback Assume that the system function for H can be written as a ratio of polynomials in R with constant, real-valued, coefficients. In this We investigate when The System H is equivalent to the following feedback system

where F is also a ratio of polynomials in R with constant, real-valued coefficients. Example 1: Systems 1 and 2 are equivalent when H = H1 = Example 2: Systems 1 and 2 are equivalent when H = H2 = 5.1 Generalization Which of the following expressions for F guarantees equivalence of Systems 1 and 2? Enter FA or FB or FC or FD or None: FC Let E represent the output of the adder. Then Y = FE = F(X + Y) Y − FY = FX

H − HF = F H = F + HF 5.2 Find the Poles Let H3 = Determine the pole(s) of H3 and the pole(s) of Pole(s) of H3: -1/2 Pole(s) of 1/7 Substitute 1/ z for R in H3: The denominator has a root at z = −1/2. Therefore there is a pole at −1/2. Substitute H3 into FB3:

Now substitute 1/ z for R: The denominator has a root at z = 1/7. Therefore there is a pole at 1/7. 5.3 SystemFunction Write a procedure insideOut(H): • the input H is a sf.SystemFunction that represents the system H, and • the output is a sf.SystemFunction that represents You may use the SystemFunction class and other procedures in sf: Attributes and methods of SystemFunction class:

__init__(self, numPoly, denomPoly) poles(self) poleMagnitudes(self) dominantPole(self) numerator denominator Procedures in sf sf.Cascade(sf1, sf2) sf.FeedbackSubtract(sf1, sf2) sf.FeedbackAdd(sf1, sf2) sf.Gain(c) def insideOut(H): return sf.FeedbackAdd(H, sf.Gain(1)) or return sf.SystemFunction(H.numerator,H.denominator-H.numerator) Robot SM: Reference Sheet

In Design Lab 2, we developed a state machine for getting the robot to follow boundaries. Here, we will develop a systematic approach for specifying such state machines. We start by defining a procedure called inpClassifier, which takes an input of type io.SensorInput and classifies it as one of a small number of input types that can then be used to make decisions about what the robot should do next. Recall that instances of the class io.SensorInput have two attributes: sonars, which is a list of 8 sonar readings and odometry which is an instance of util.Pose, which has attributes x, y and theta. Here is a simple example: def inpClassifier(inp): if inp.sonars[3] < 0.5: return ’frontWall’ elif inp.sonars[7] < 0.5: return ’rightWall’ else: return ’noWall’ Next, we create a class for defining “rules.” Each rule specifies the next state, forward velocity and rotational velocity that should result when the robot is in a specified current state and receives a particular type of input. Here is the definition of the class Rule:

class Rule: def __init__(self, currentState, inpType, nextState, outFvel, outRvel): self.currentState = currentState self.inpType = inpType self.nextState = nextState self.outFvel = outFvel self.outRvel = outRvel Thus, an instance of a Rule would look like this: Rule(’NotFollowing’, ’frontWall’, ’Following’, 0.0, 0.0) which says that if we are in state ’NotFollowing’ and we get an input of type ’frontWall’, we should transition to state ’Following’ and output zero forward and rotational velocities. Finally, we will specify the new state machine class called Robot, which takes a start state, a list of Rule instances, and a procedure to classify input types. The following statement creates an instance of the Robot class that we can use to control the robot in a Soar brain.

r = Robot(’NotFollowing’, [Rule(’NotFollowing’, ’noWall’, ’NotFollowing’, 0.1, 0.0), Rule(’NotFollowing’, ’frontWall’, ’Following’, 0.0, 0.0), Rule(’Following’, ’frontWall’, ’Following’, 0.0, 0.1)], inpClassifier) Assume it is an errorif a combination of state and input type occurs that is not covered in the rules. In that case, the state will not change and the output will be an action with zero velocities.

Quality Python Homework Help

More Related Content

What's hot

Similar to Quality Python Homework Help

More from Python Homework Help

Recently uploaded

Quality Python Homework Help