Simulation of convolutional encoder

Simulation of convolutional encoder

• 1.
  IJRET: International Journalof Research in Engineering and Technology eISSN: 2319-1163 | pISSN: 2321-7308 __________________________________________________________________________________________ Volume: 03 Issue: 03 | Mar-2014, Available @ http://www.ijret.org 557 SIMULATION OF CONVOLUTIONAL ENCODER Sneha Bawane1 , V.V.Gohokar2 1 M.E student, Dept of Electronics and Telecommunication, SSGMCE Shegaon, Maharashtra-444203, India 2 Professor, Dept of Electronics and Telecommunication, SSGMCE Shegaon, Maharashtra-444203, India Abstract Convolutional encoding is a Forward Error Correction (FEC) technique used in continuous one-way and real time communication links. Wireless devices such as hand phones and broadband modems rely heavily on forward error correction techniques for their proper functioning, thus sending and receiving information with minimal or no error, while utilizing the available bandwidth. Major requirements for modern digital wireless communication systems include high throughput, low power consumption and physical size. This paper presents the simulation of convolutional encoder using MATLAB. The performance and analysis has done by changing rates of convolutional encoder and error of binary symmetric channel. Keywords: Constraint Length, Convolutional Encoder, Data rates, Generator polynomials, Poly2trellis structure. -----------------------------------------------------------------------***----------------------------------------------------------------------- 1. INTRODUCTION Convolutional encoding is a method of adding redundancy to a data stream in a controlled manner to give the destination the ability to correct bit errors without asking the source to retransmit. Convolutional codes, and other codes which can correct bit errors at the receiver, are called forward error correcting (FEC). The ever increasing use of wireless digital communication has led to a lot of effort invested in FEC (Forward Error Correction).Convolutional codes are introduced in 1955 by Elias. Convolutional codes are one of the powerful and widely used class of codes, These codes are having many applications, that are used in deep-space communications, voice band modems, wireless standards(such as 802.11) and in satellite communications. Convolutional codes are plays a role in low-latency applications such as speech transmission. 1.1 Convolutional Encoder The convolutional encoder maps a continuous information bit stream into a continuous bit stream of encoder output. The convolutional encoder is a finite state machine, which is a machine having memory of past inputs and also having a finite number of different states. Convolutional codes are commonly specified by three parameters; (n, k, m). n = number of output bits k = number of input bits m = number of memory registers Where, n>k The quantity k/n is called as code rate. it is a measure of the efficiency of the code . Commonly k and n parameters range from 1 to 8, m from 2 to 10 and the code rate from 1/8 to 7/8 except for deep space applications where code rates as low as 1/100 or even longer have been employed. here The quantity L is called the constraint length of the code and is defined by Constraint Length, L = k (m-1) The constraint length L represents the number of bits in the encoder memory that affect the generation of the n output bits. The constraint length L is also referred to by the capital letter K, which can be confusing with the lower case k, which represents the number of input bits. In some books K is defined as equal to product the of k and m. Often in commercial specifications, the codes are specified by (r, K), where r = the code rate k/n and K is the constraint length. 1.2 Generator Polynomials Generator Polynomial is defined by- g(i) (D)=g0 (i) +g1 (i) (D)+ g2 (i) (D2 )+……..+gM (i) (DM ) Where, D = unit delay variable M = number of stages of shift registers.
• 2.
  IJRET: International Journalof Research in Engineering and Technology eISSN: 2319-1163 | pISSN: 2321-7308 __________________________________________________________________________________________ Volume: 03 Issue: 03 | Mar-2014, Available @ http://www.ijret.org 558 Example:- Fig-1: Convolutional Encoder From above the generator polynomials codes are- G1=133(OCT) and G2=171(OCT) G1=x0+x2+x3+x5+x6 =1011011=133(OCT) G2=x0+x1+x2+x3+x6 =1111001=171(OCT) 1.3. Poly2trellis Syntax: trellis=poly2trellis( ConstraintLength, CodeGenerator) The poly2trellis function accepts a polynomial description of a convolutional encoder and returns the corresponding trellis structure description. The output of poly2trellis is suitable as an input to the convenc and vitdec functions, and as a mask parameter for the Convolutional Encoder, Viterbi Decoder in the Communications Blockset. Trellis=poly2trellis (ConstraintLength, CodeGenerator) Performs the conversion for a rate k/n feedforward encoder. Constraint Length is a 1-by-k vector that specifies the delay for the encoder's k input bit streams. Code Generator is a k-by- n matrix of octal numbers that specifies the n output connections for each of the encoder's k input bit streams. 2. PERFORMANCE ANALYSIS OF CONVOLUTIONAL ENCODER 2.1 Rate 1/2 Convolutional Encoder Fig-2(a): trellis= poly2trellis (3, [7 5]) From the above diagram it shows 3 shift-registers where the first one takes the incoming data bit and the rest, form the memory of the encoder. When we perform Exclusive ORing we get the generator polynomials as- G1=111=7 and G2=101=5, it shows trellis =poly2trellis(3,[7 5]) If suppose input code is 11, we have- First Step: Initially if S0=0 S1=0 and S2=0 then the coded bits are- First coded bit= 0 XOR 0 XOR 0 = 0 Second coded bit = 0 XOR 0 = 0 Thus, if input=0 then output=00 ,it shows output for rate ½ convolutional encoder. Second Step: If input =1 , shift registers perform shifting and we get S0=1 S1=0 and S2=0 First coded bit= 1 XOR 0 XOR 0 = 1 Second coded bit = 1 XOR 0 = 1 Thus, if input=1 then output=11 Third Step: Similarly if input=1, then S0=1 S1=1 and S2=0 First coded bit= 1 XOR 1 XOR 0 = 0 Second coded bit = 1 XOR 0 = 1 Thus, if input= 1 then output=01
• 3.
  IJRET: International Journalof Research in Engineering and Technology eISSN: 2319-1163 | pISSN: 2321-7308 __________________________________________________________________________________________ Volume: 03 Issue: 03 | Mar-2014, Available @ http://www.ijret.org 559 Same performance has done by using different poly2trellis, constraint length and data rates of convolutional encoder. 2.2 Rate 1/3 Convolutional Encoder g1 = 111, g2 = 011, g3=101 Fig-2(b): trellis = poly2trellis (3, [7 3 5]) 2.3. Rate 2/3 Convolutional Encoder Fig-2(c): trellis=poly2trellis ([5 4], 23 35 0; 0 5 13) The first paragraph under each heading or subheading should be flush left, and subsequent paragraphs should have a five- space indentation. A colon is inserted before an equation is presented, but there is no punctuation following the equation. All equations are numbered and referred to in the text solely by a number enclosed in a round bracket (i.e., (3) reads as "equation 3"). Ensure that any miscellaneous numbering system you use in your paper cannot be confused with a reference [4] or an equation (3) designation. 3. SIMULATION Fig-3: Simulink Model
• 4.
  IJRET: International Journalof Research in Engineering and Technology eISSN: 2319-1163 | pISSN: 2321-7308 __________________________________________________________________________________________ Volume: 03 Issue: 03 | Mar-2014, Available @ http://www.ijret.org 560 Fig-3(a): Simulation results by changing encoder with same BSC error Fig-3(b): Simulation results by changing error of BSC with same encoder
• 5.
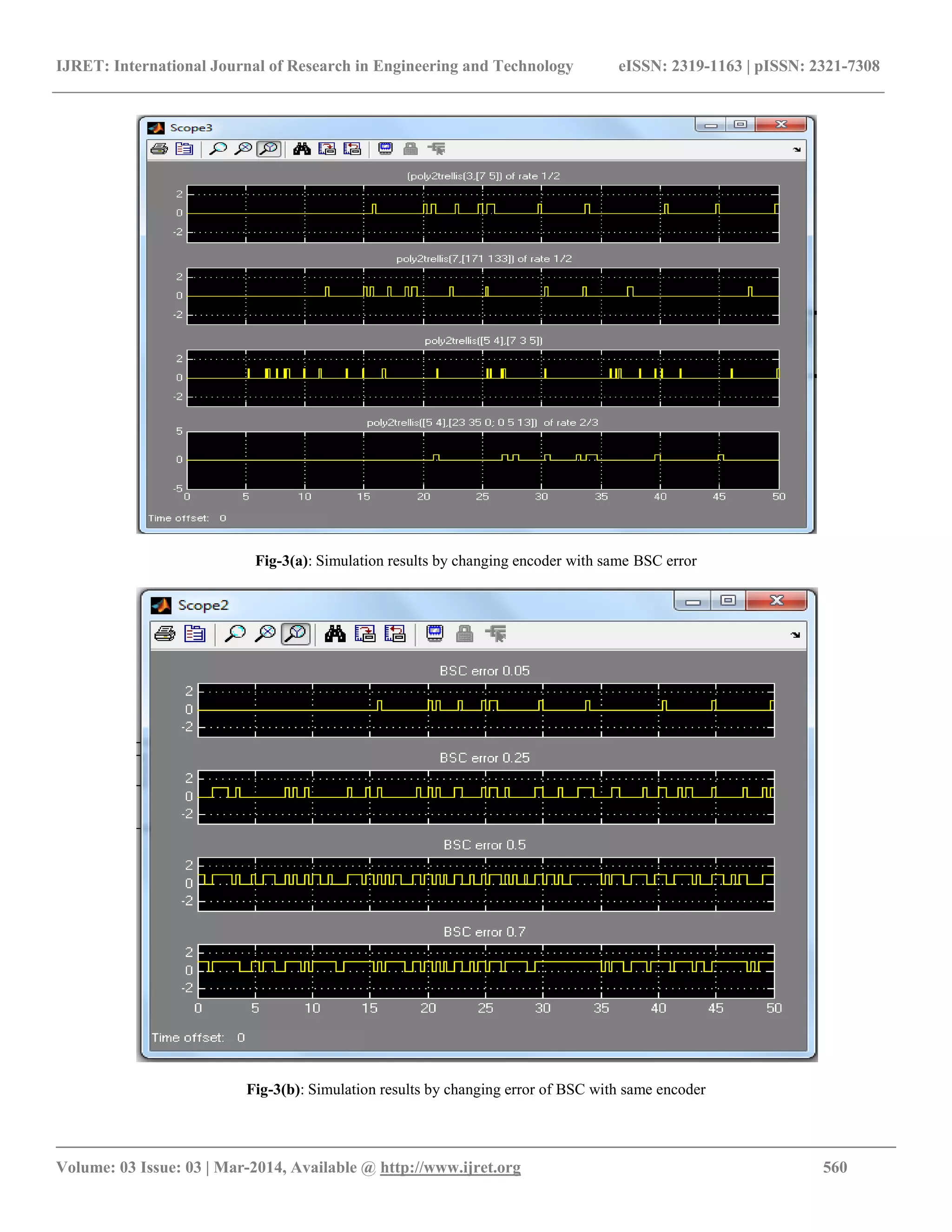
  IJRET: International Journalof Research in Engineering and Technology eISSN: 2319-1163 | pISSN: 2321-7308 __________________________________________________________________________________________ Volume: 03 Issue: 03 | Mar-2014, Available @ http://www.ijret.org 561 4. CONCLUSIONS Simulation has done by using MATLAB .When signal to noise ratio changes the change in the output of convolutional encoder occurs. From the above results,[3(a)] by keeping signal to noise ratio constant and by changing data rates of convolutional encoder it can be seen that rate 2/3 gives better result than 1/2 and 1/3 and [3(b)] by keeping date rate 1/2 and changing signal to noise ratio it shows that with the minimum S/N ratio it gives better result. REFERENCES [1]. Yan Sun1, Zhizhong Ding2, “ FPGA Design and Implementation of a Convolutional Encoder and a Viterbi Decoder Based on 802.11a for OFDM”, Received March 5th, 2012; revised April 1st, 2012; accepted April 9th, 2012, doi:10.4236/wet.2012.33019. [2]. Zafar Iqbal, Saeid Nooshabadi, Heung-No Lee, “Analysis and Design of Coding and Interleaving in a MIMO-OFDM Communication System”, Vol. 58, No. 3, August 2012. [3]. JOHN WILEY, “ERROR CONTROL CODING”, Peter Sweeney, University of Surrey, Guildford, UK [4]. A. Msir, F. Monteiro*, A. Dandache, B. Lepley, “Design of a high speed parallel encoder for convolutional codes”, Microelectronics Journal 35 (2004) 151–166. BIOGRAPHIES Sneha W. Bawane is a M.E student in Digital Electronics in S.S.G.M.C.E., Shegaon, Maharashtra. She received the BE degree in Electronics Engineering from RTM Nagpur university. Her current research interests include design of convolutional encoder. Vinaya V. Gohokar working as Professor in department of Electronics and Telecommunication Engineering, S.S.G.M.C.E., Shegaon, Maharashtra She received her PhD from Amaravati University in the field of video processing. Her areas of interest are image and video processing, microwave communication and signal processing.