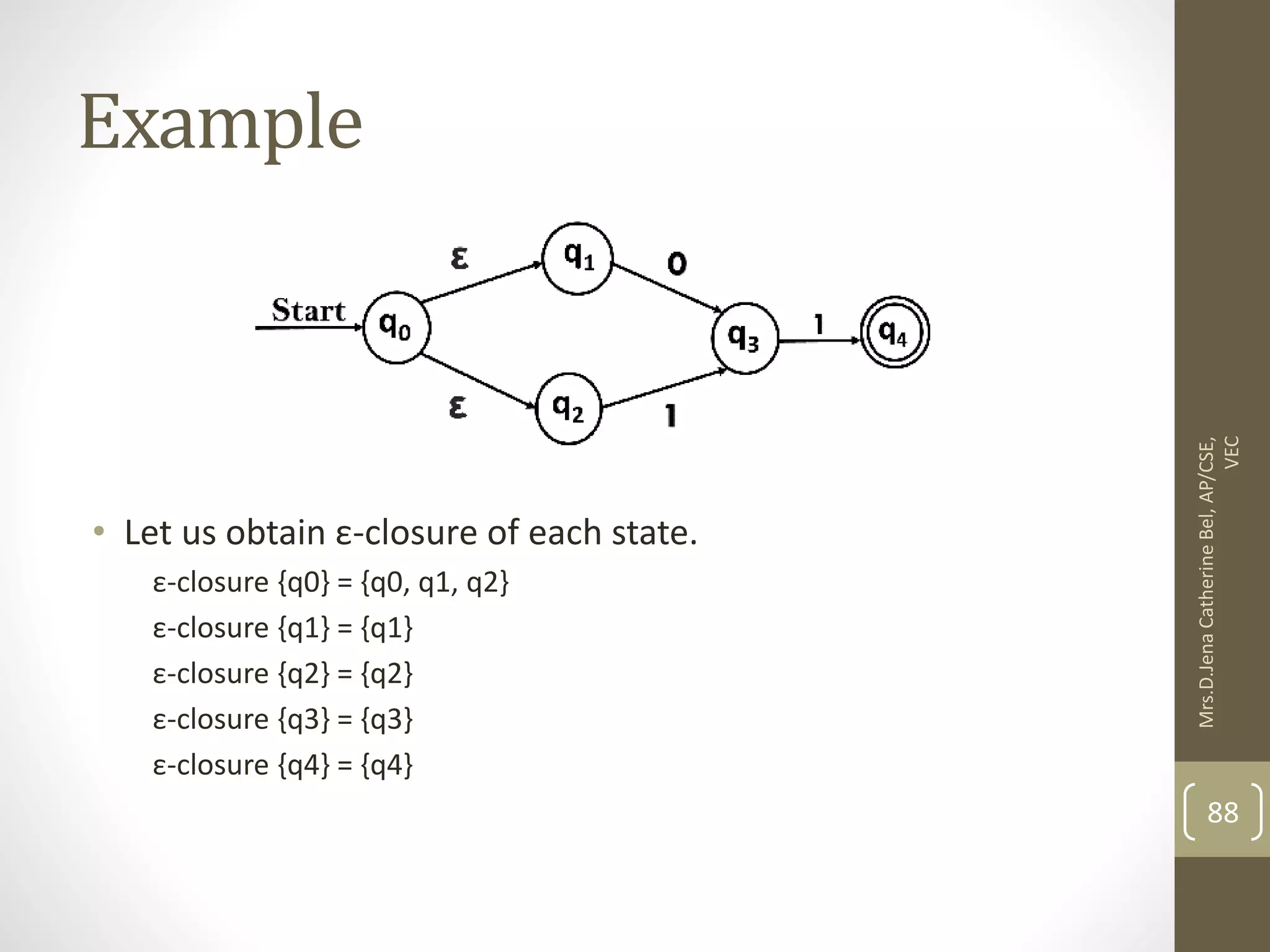
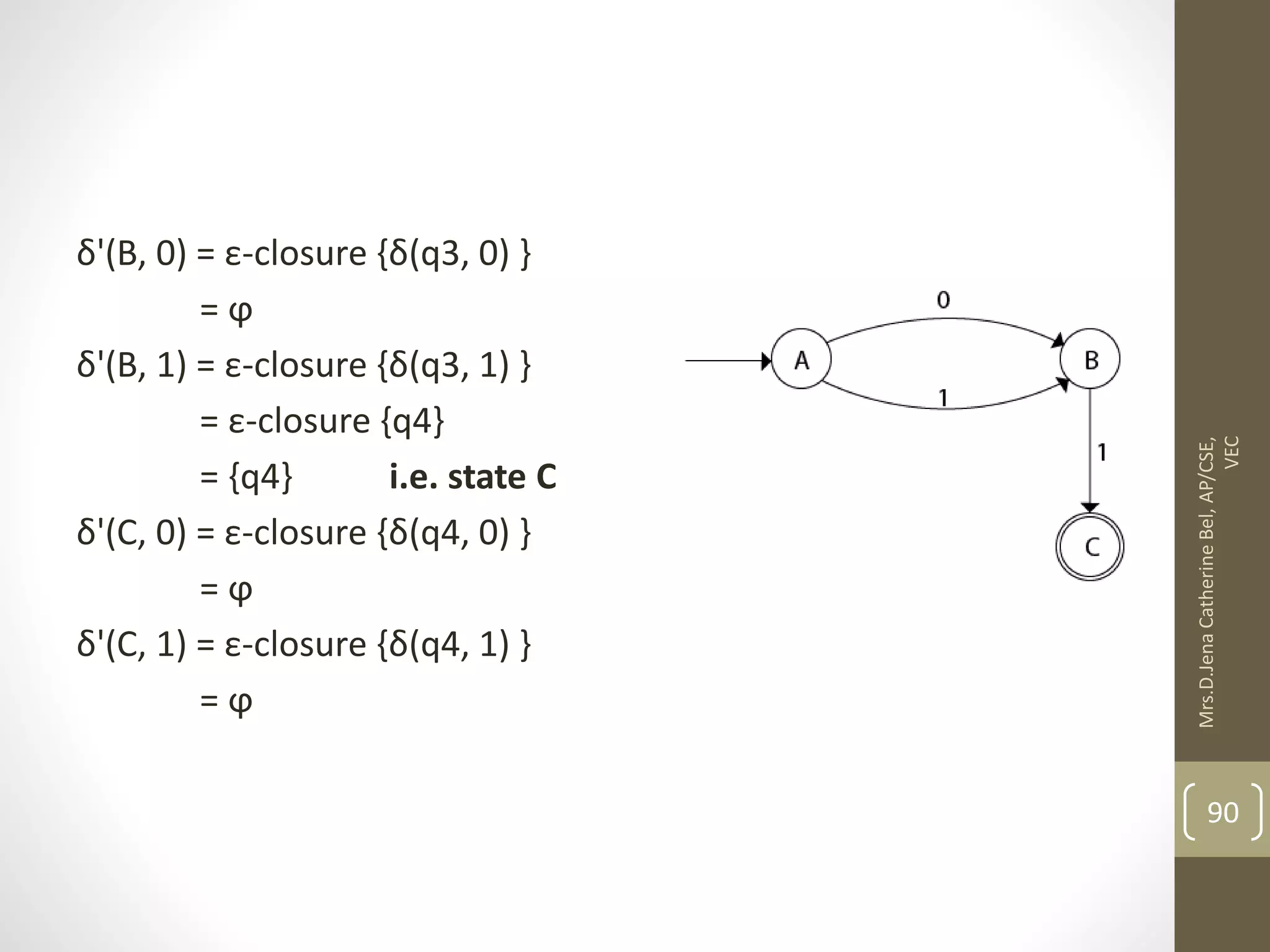
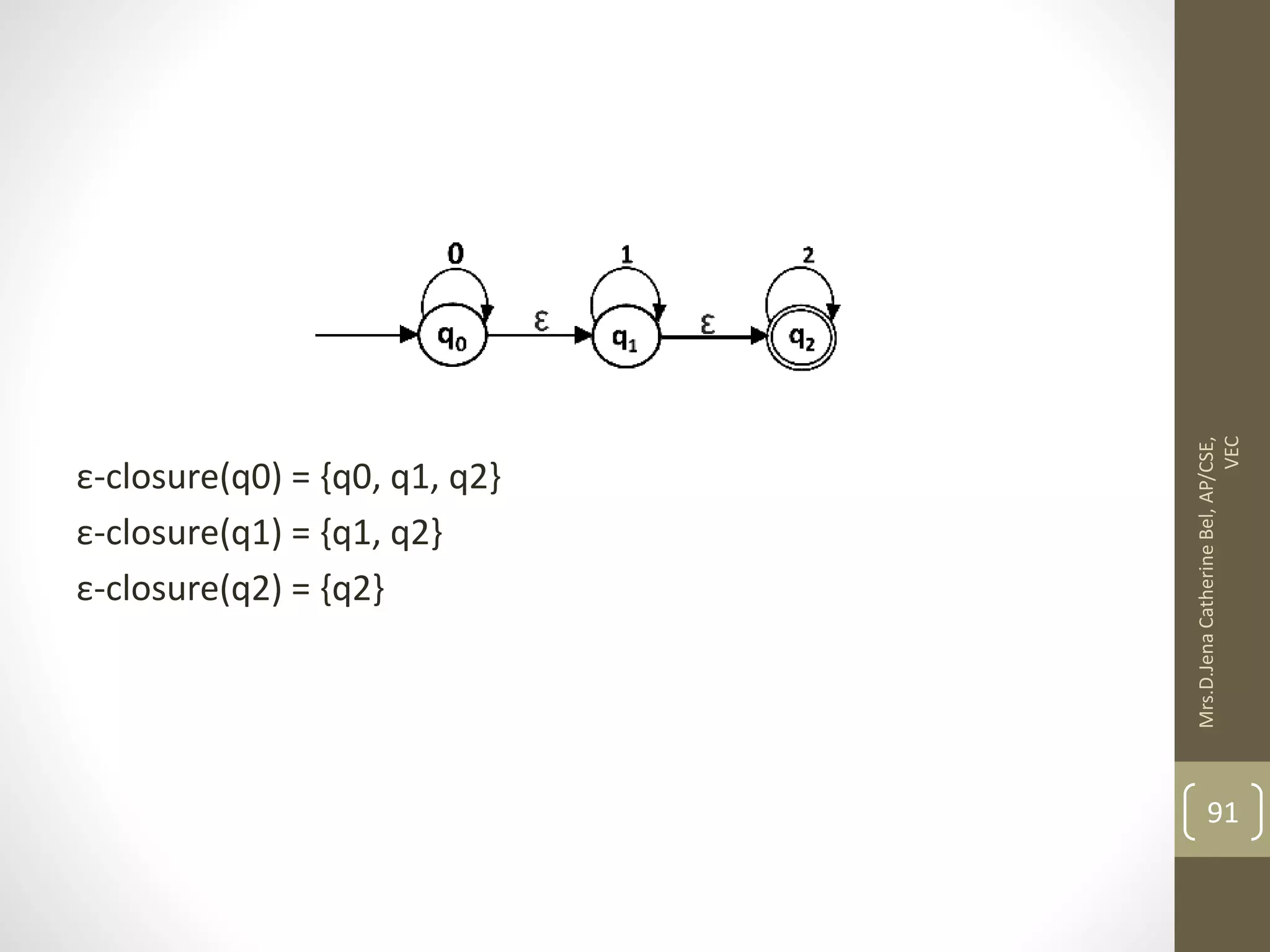
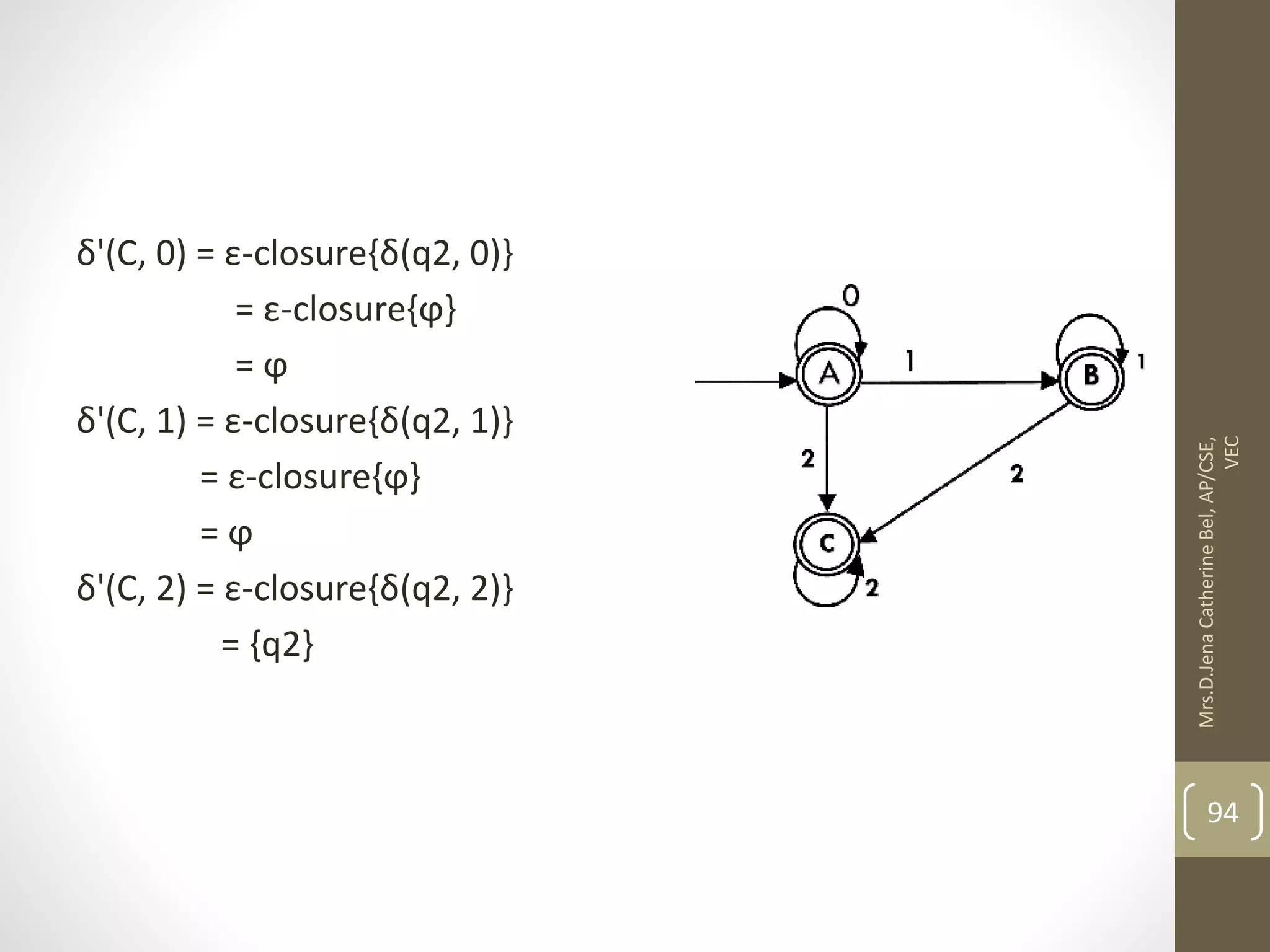
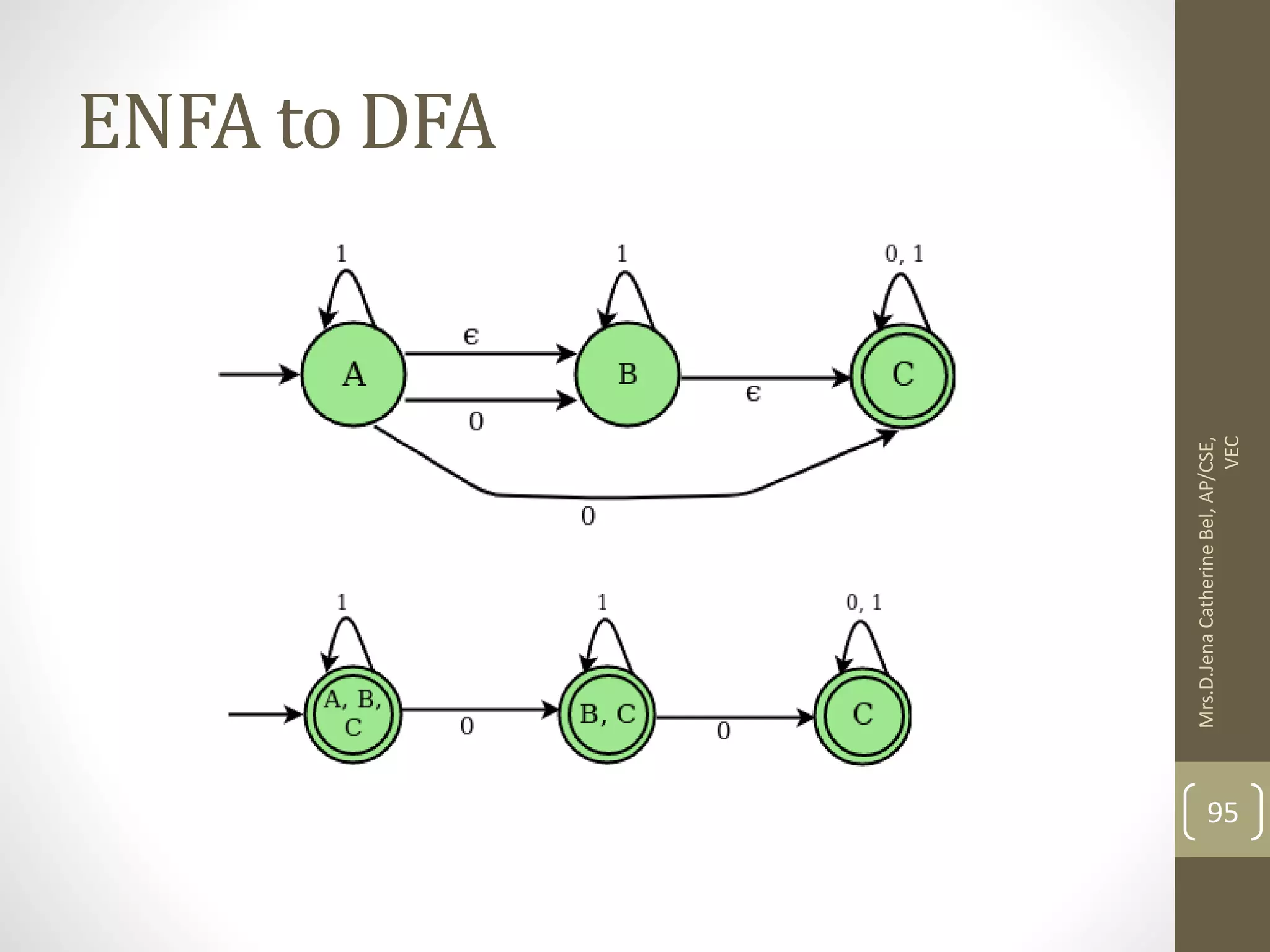
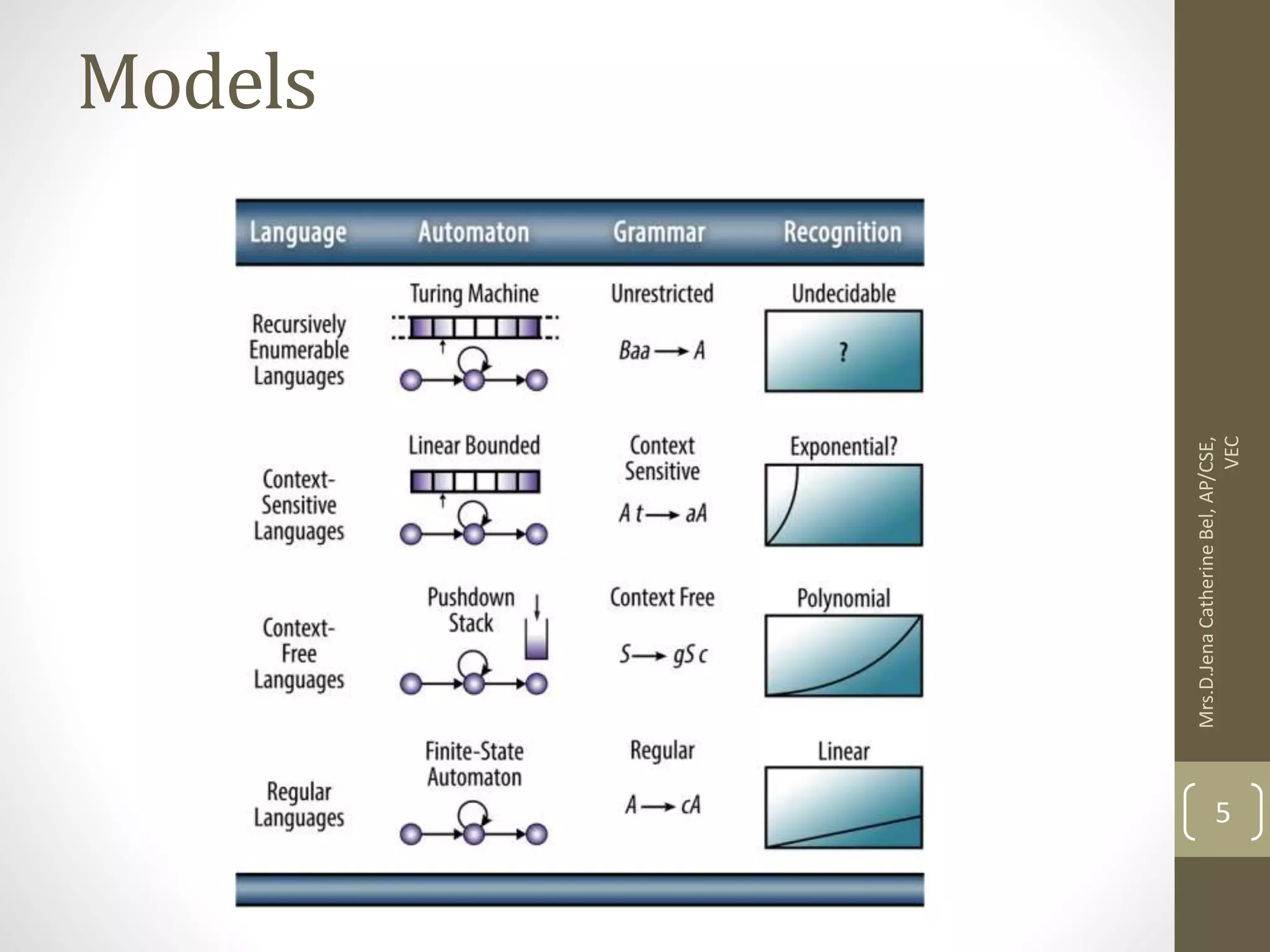
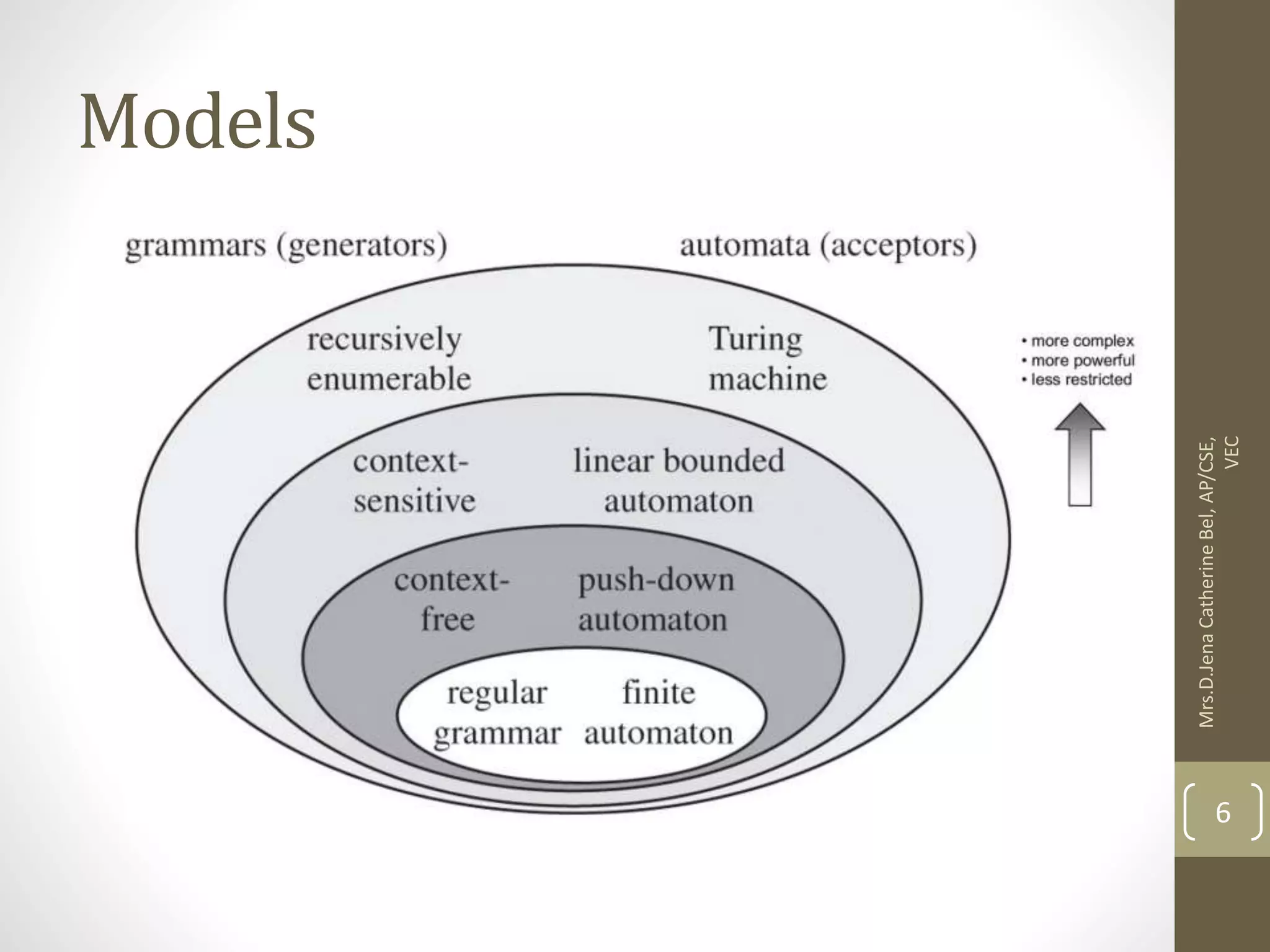
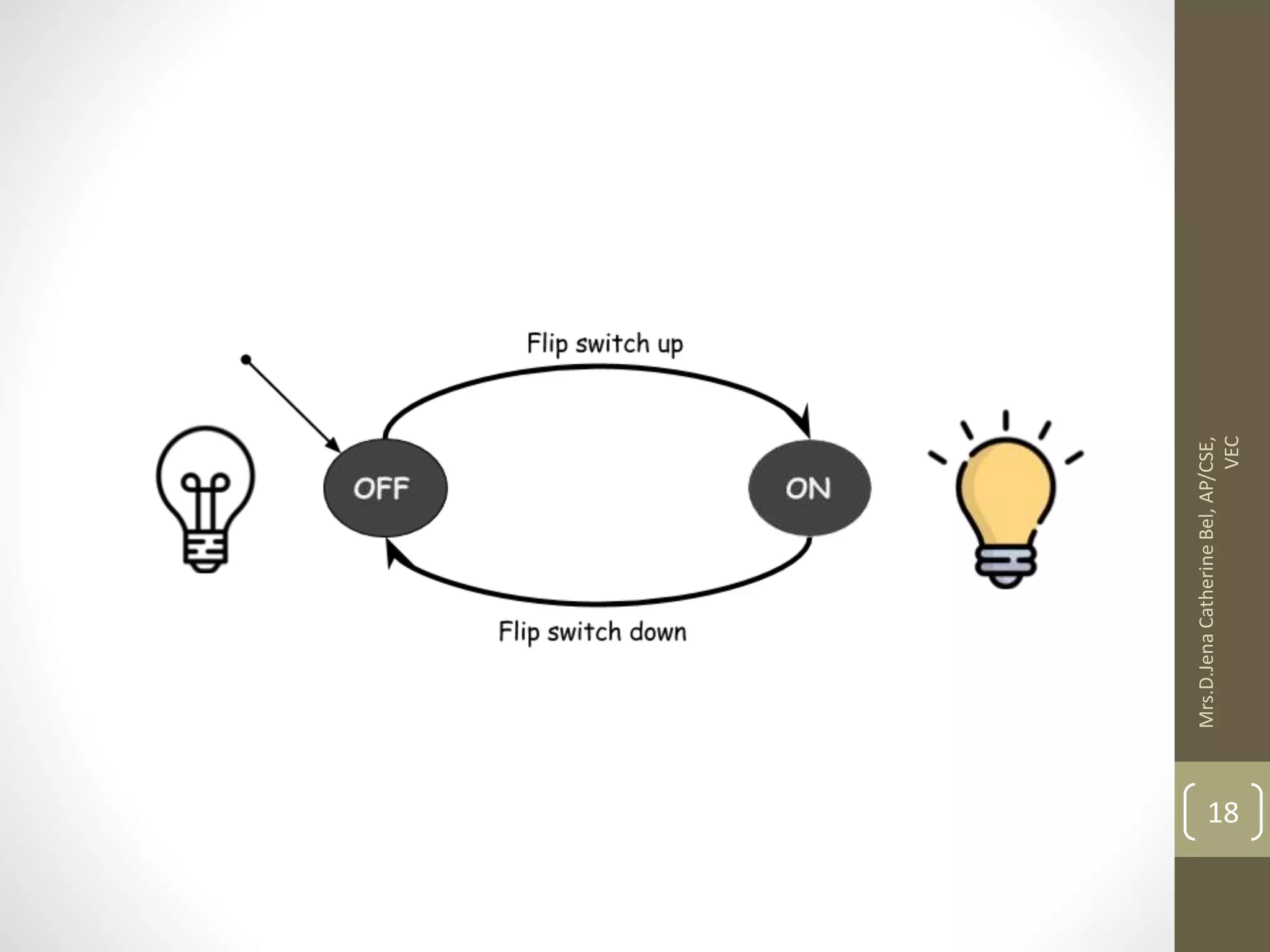
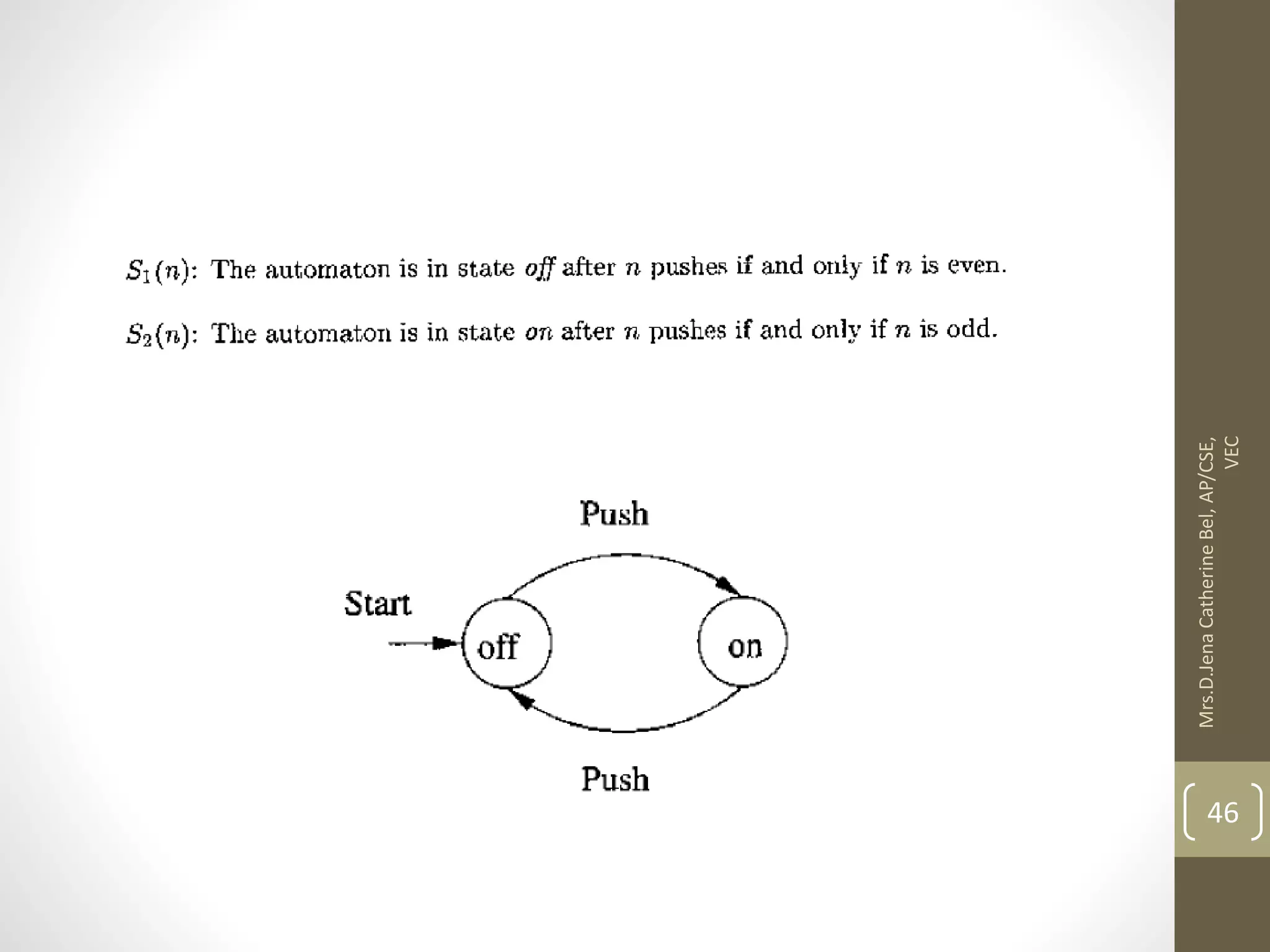
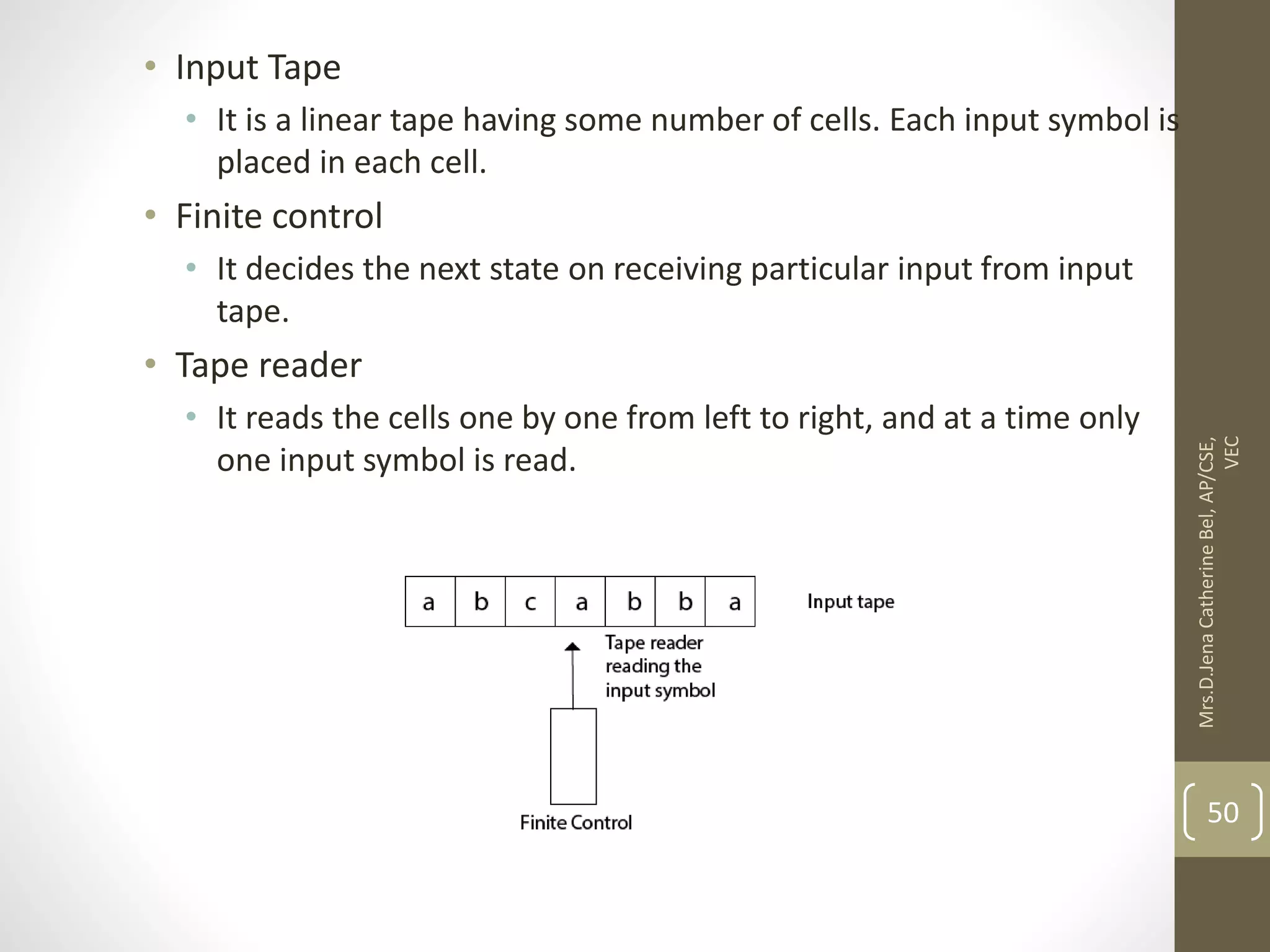
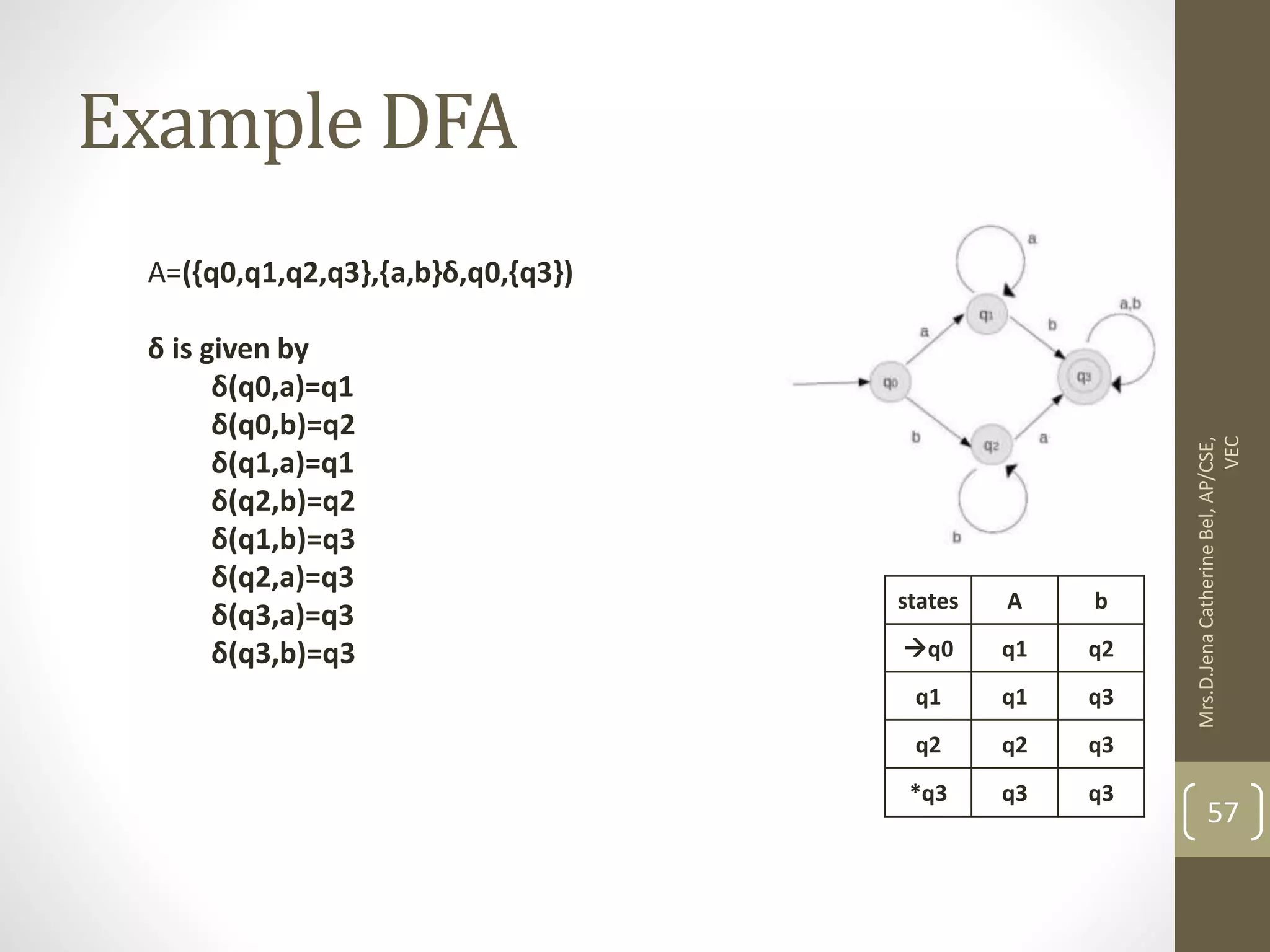
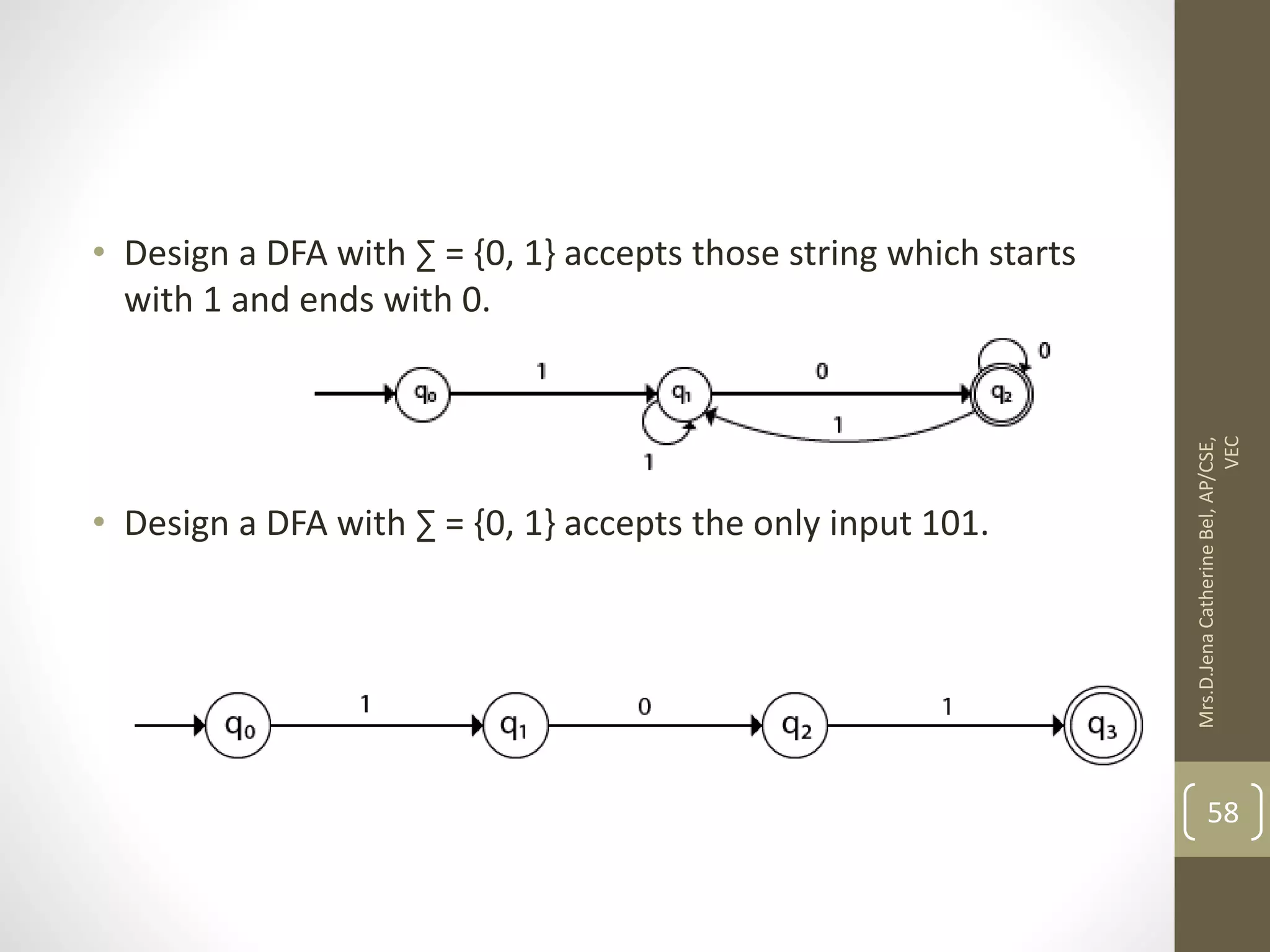
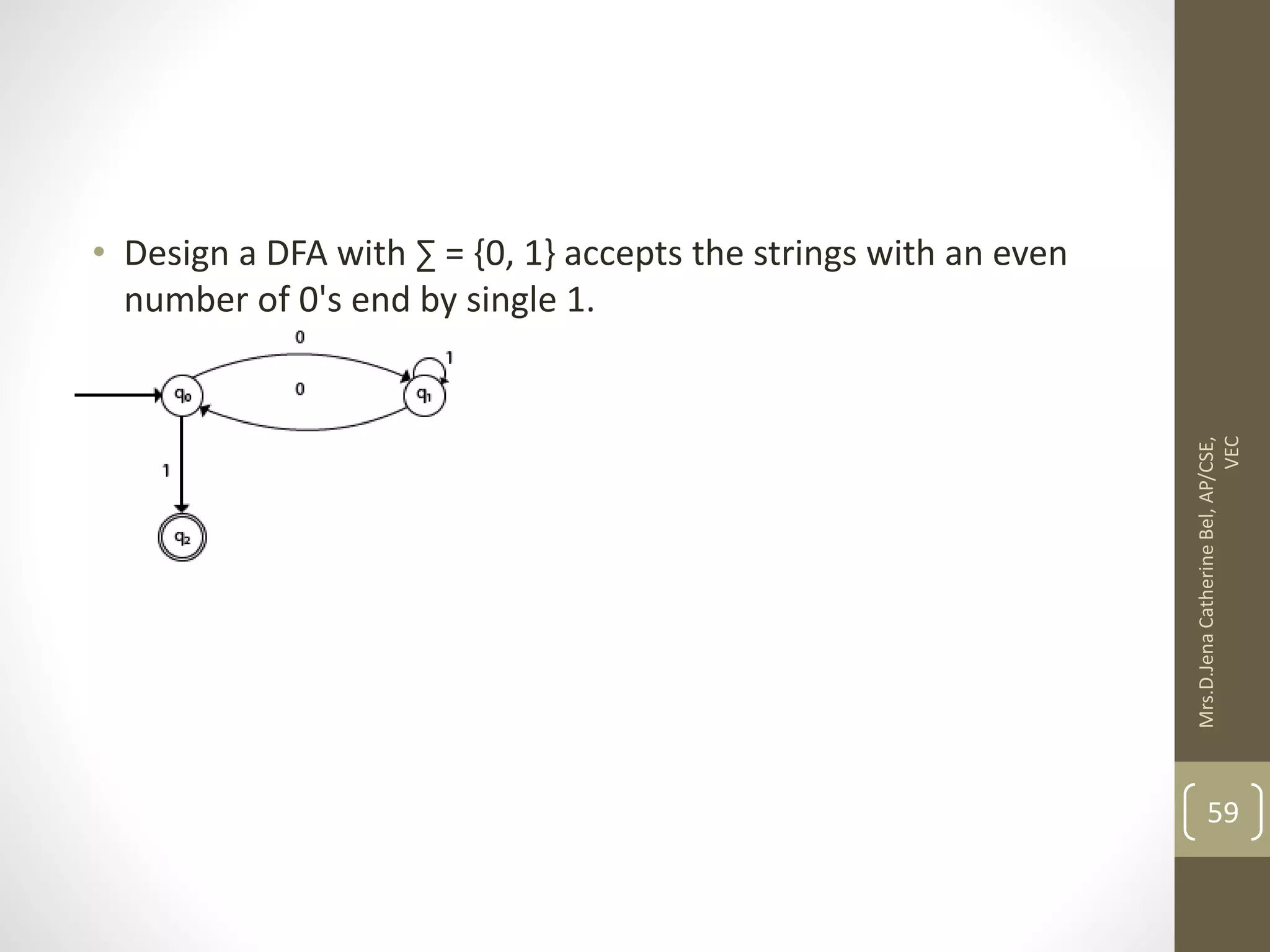
This document describes a course on Theory of Computation. It provides information on the course objectives, which are to understand language hierarchies, construct automata for patterns, design context-free grammars, understand Turing machines and their capabilities, and understand undecidable and NP problems. It outlines 5 units that will be covered: automata fundamentals, regular expressions and languages, context-free grammar and languages, properties of context-free languages, and undecidability. It also provides the course outcomes and lists reference textbooks. The document then begins describing some key concepts from Unit 1, including formal proofs, additional proof forms, inductive proofs, and an introduction to finite automata.













![Example • English • Alphabet – [a-z] • String –{hi,hello,…} • Binary number • Alphabet – [0,1] • String –{0,1,00,01,10,11…} • Hexadecimal • Alphabet –[0-9][a-e] • String –[0,1,1A3,…] 16 Mrs.D.Jena Catherine Bel, AP/CSE, VEC](https://image.slidesharecdn.com/fullunit1-220307085807/75/Theory-of-Computation-Unit-1-16-2048.jpg)




















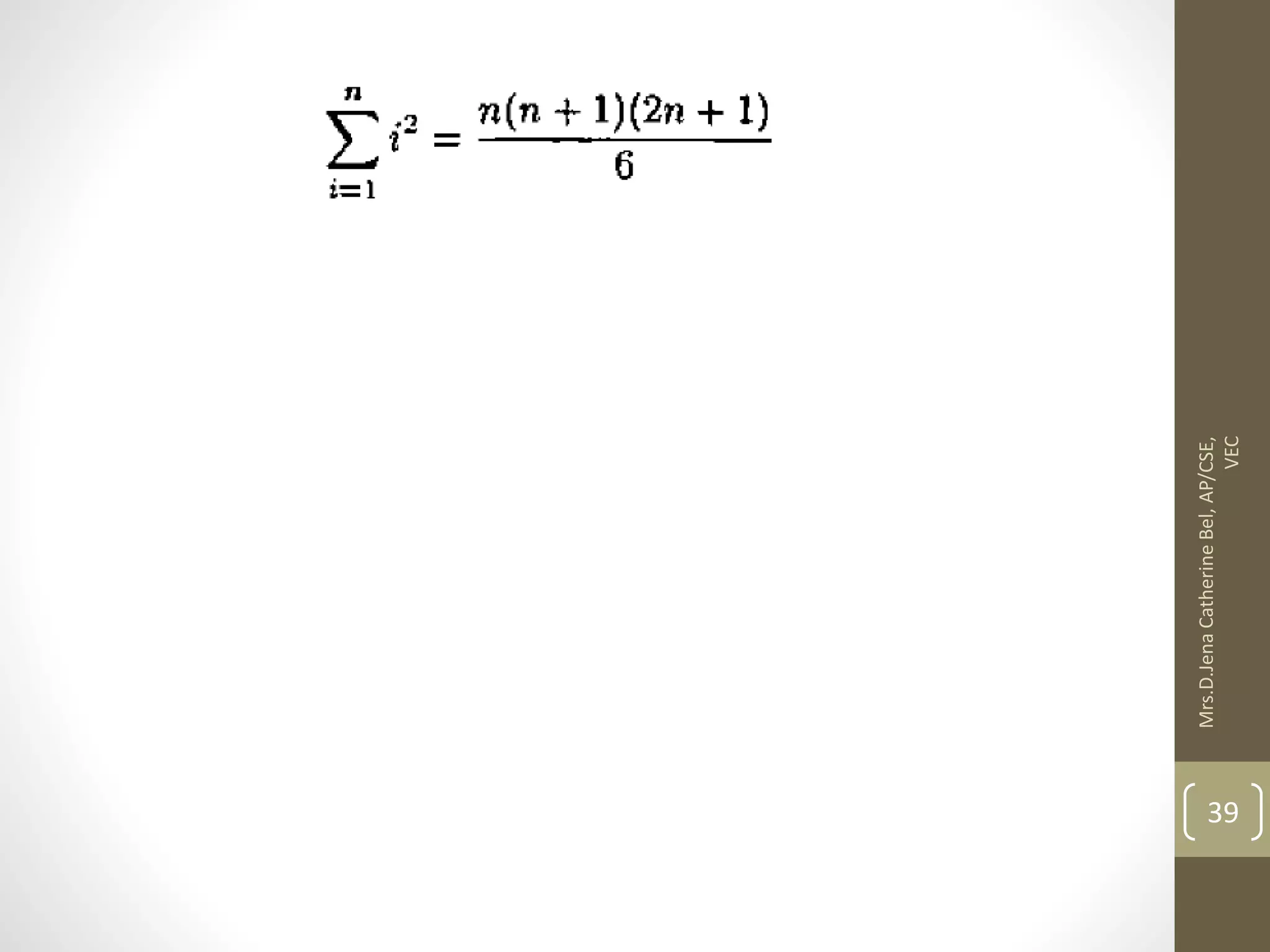
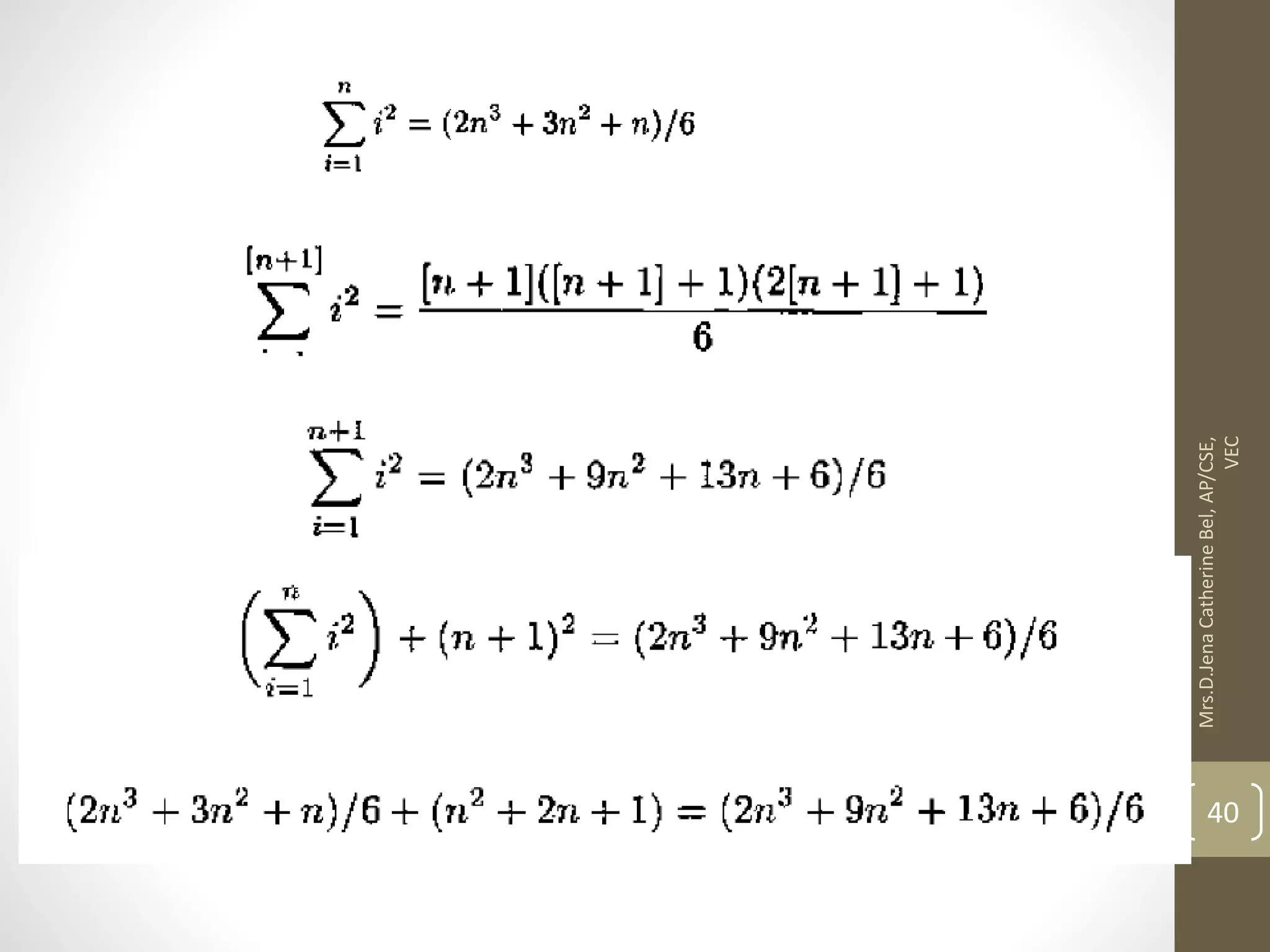




















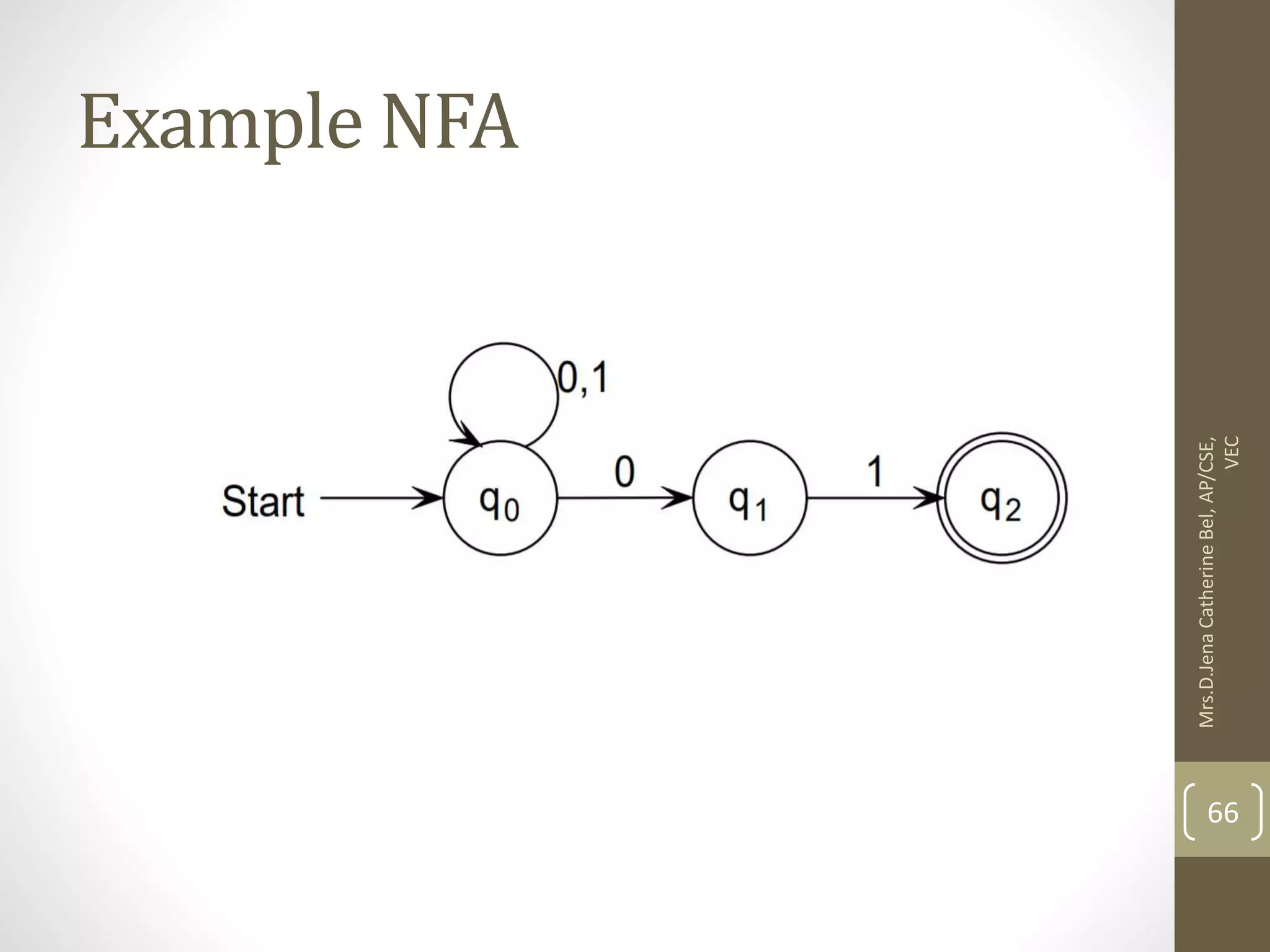
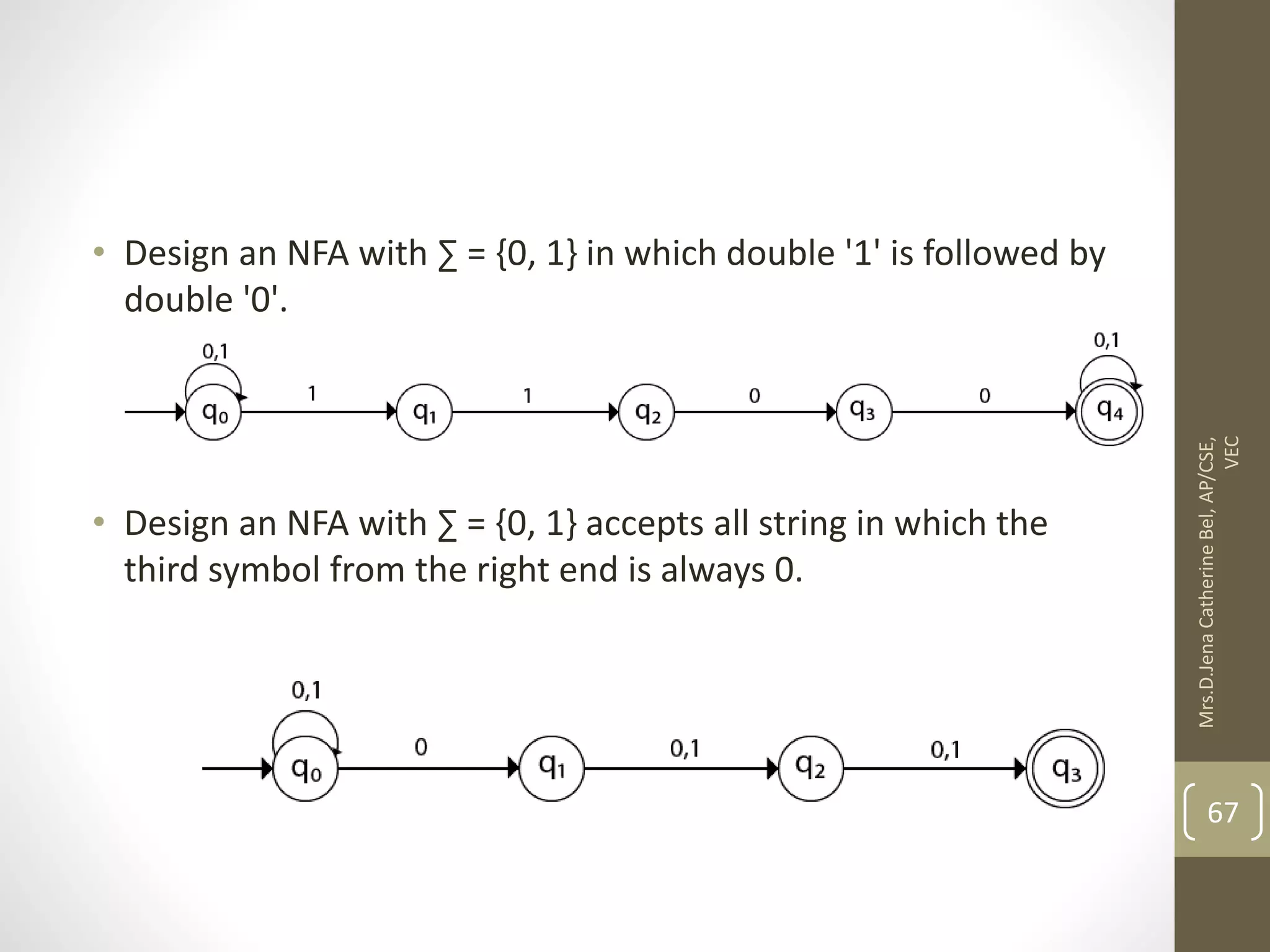



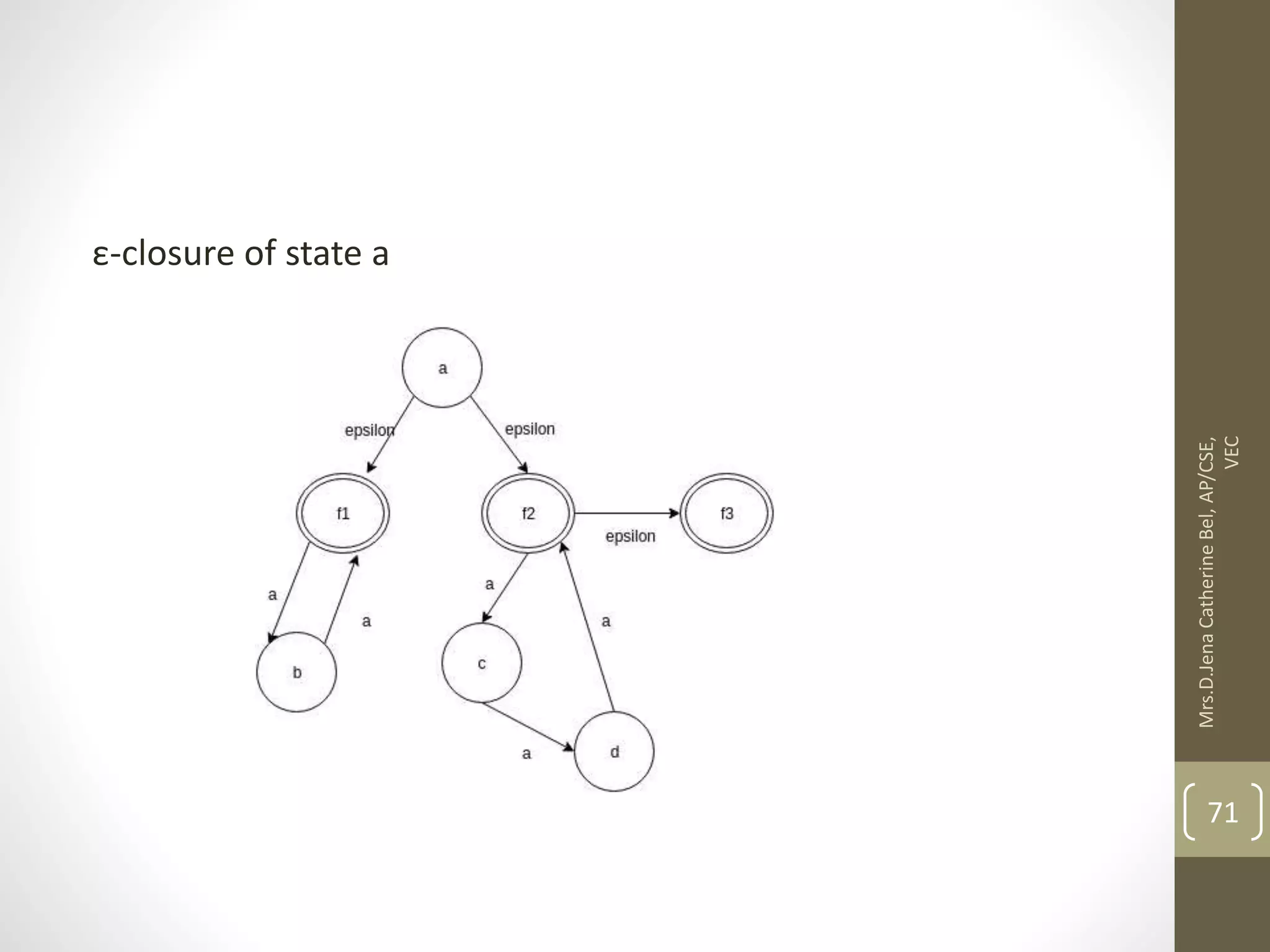
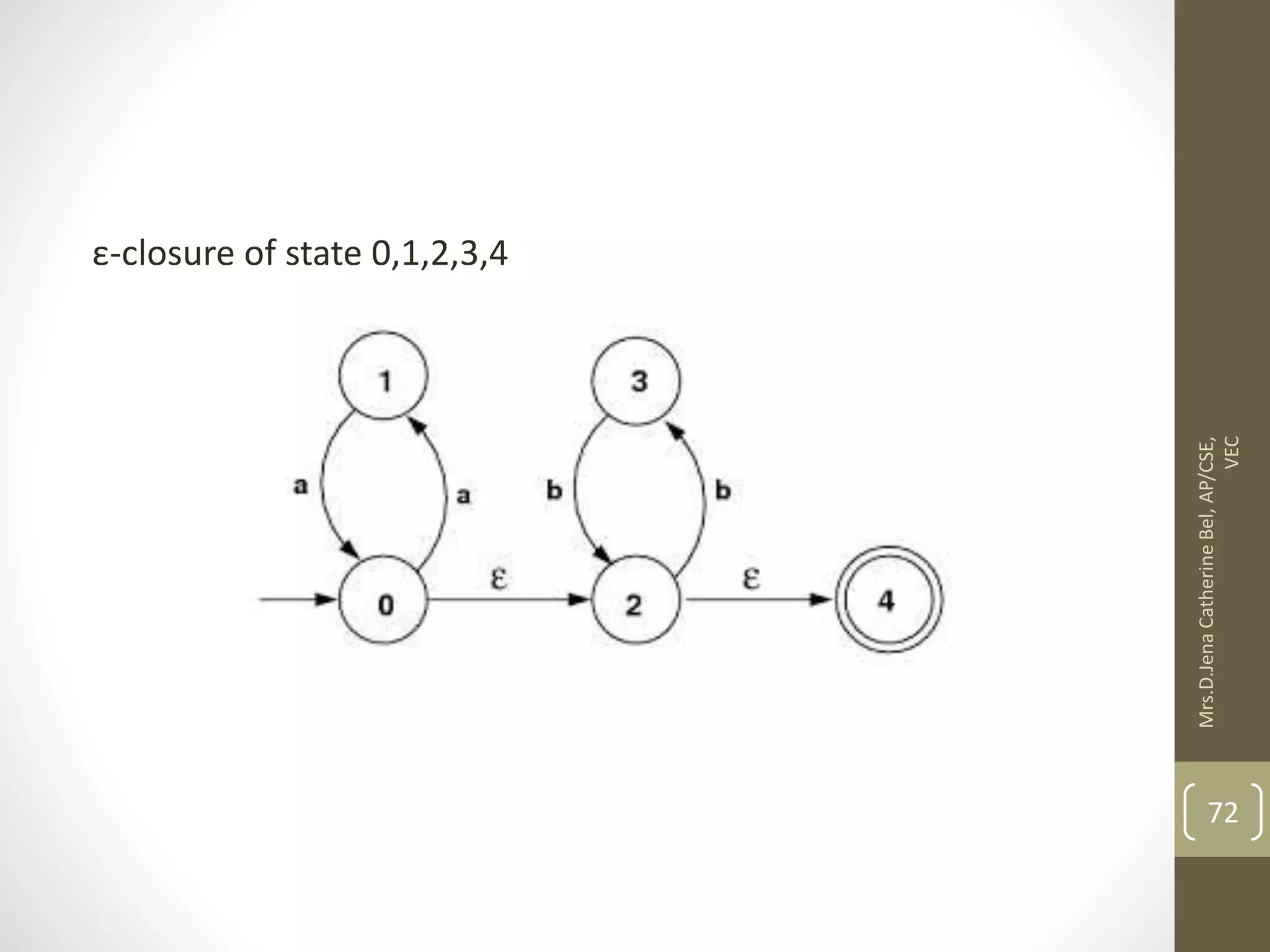




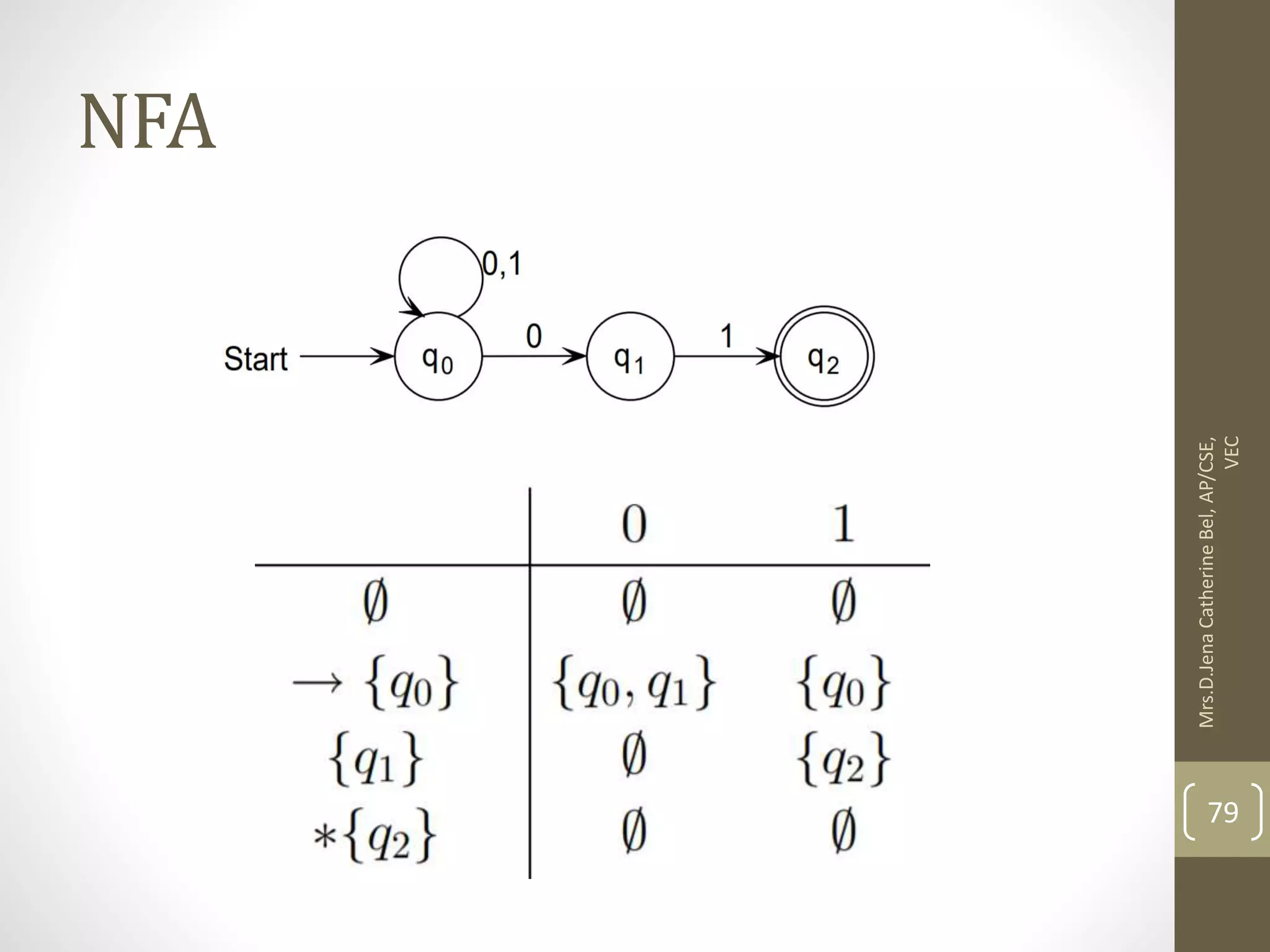

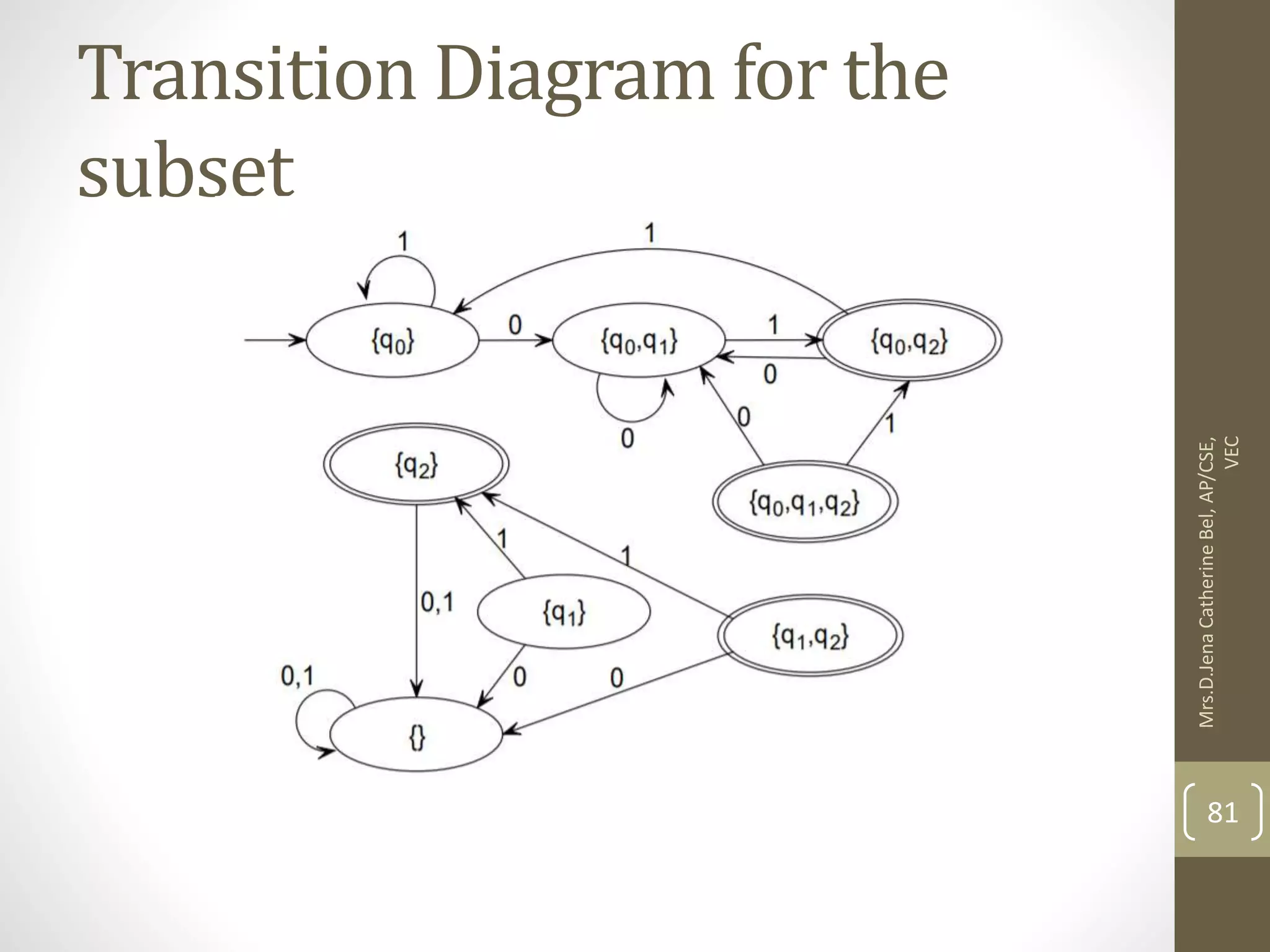
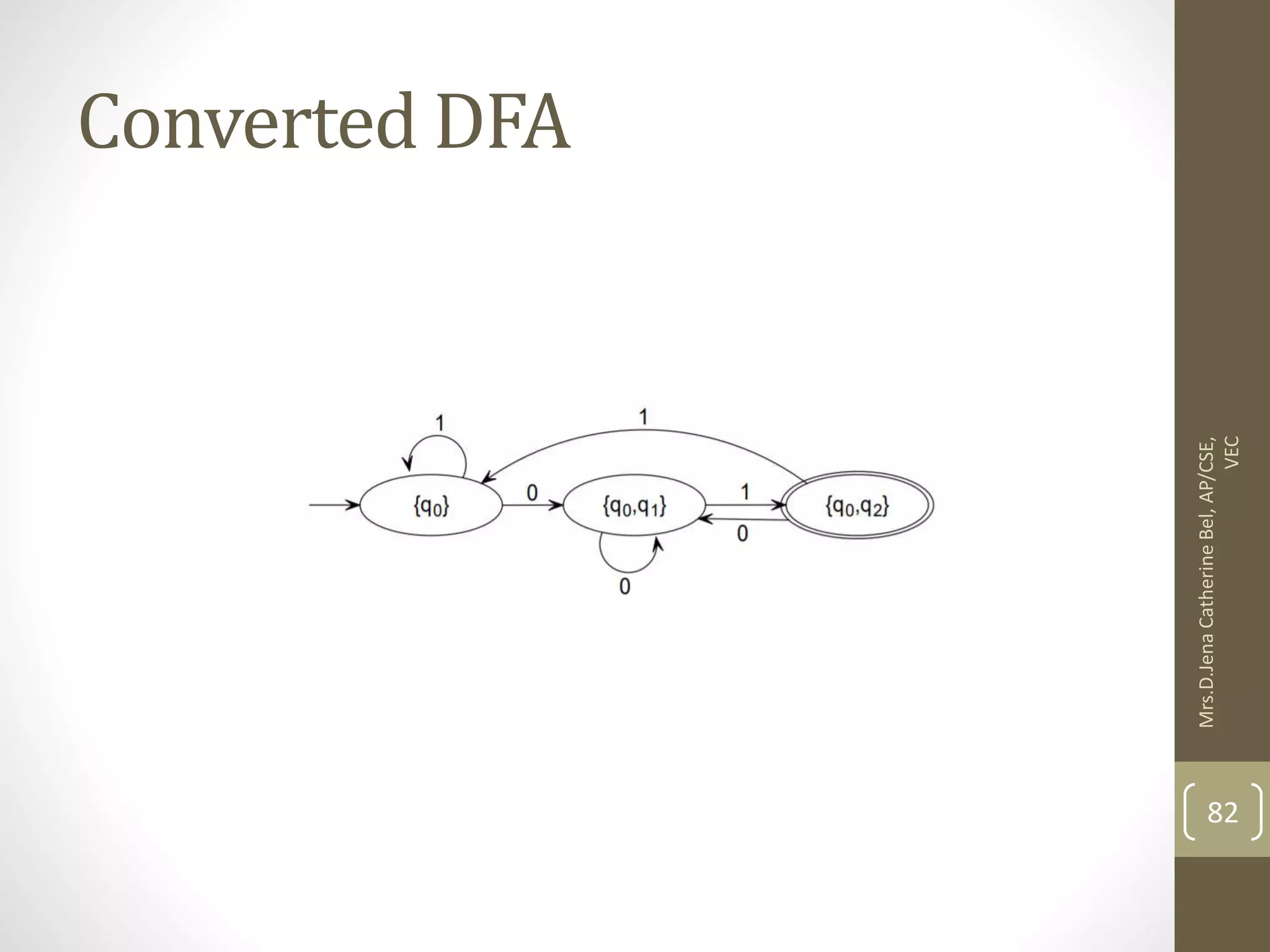
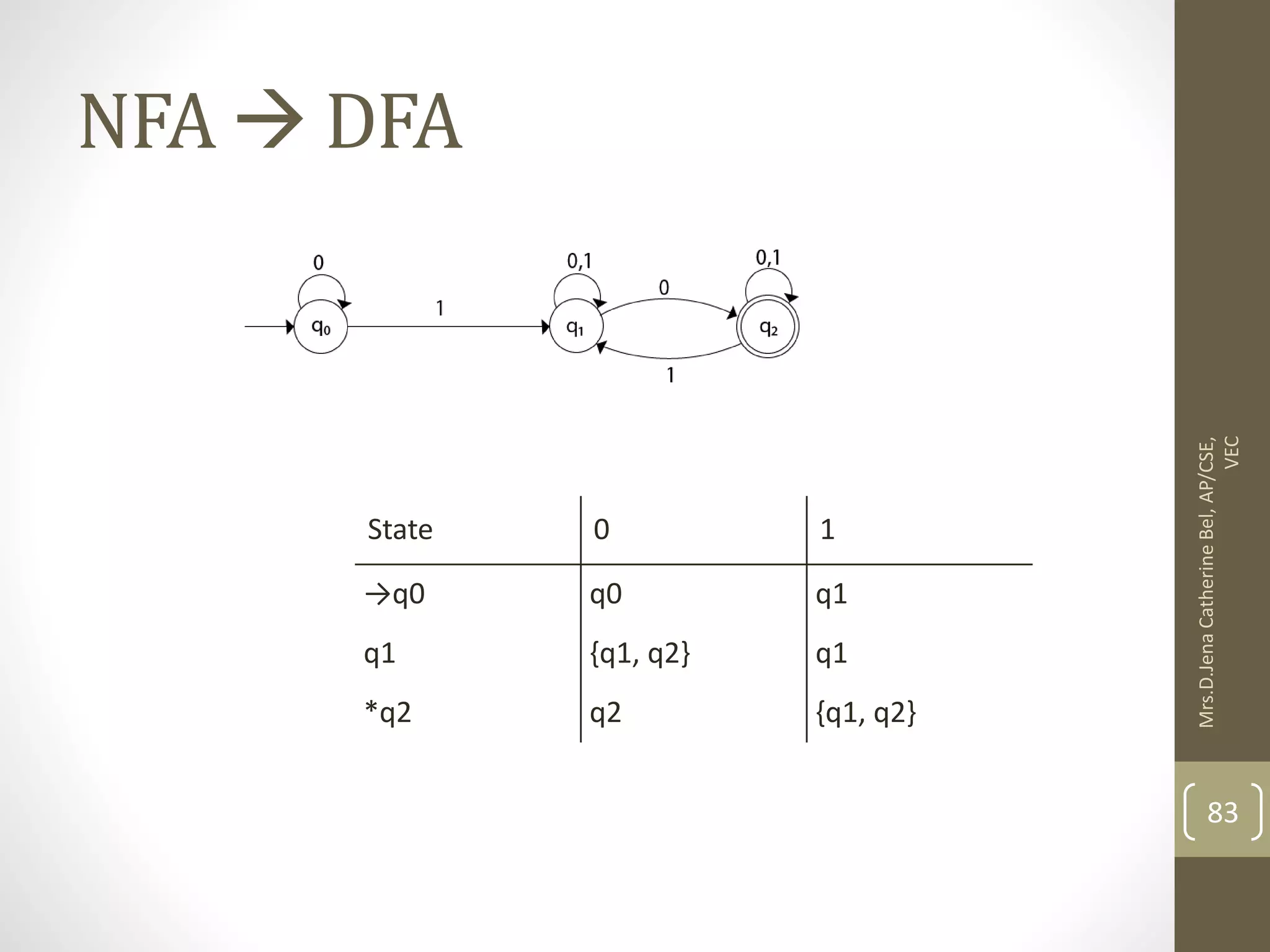
![Now we will obtain δ' transition for state q0. δ'([q0], 0) = [q0] δ'([q0], 1) = [q1] The δ' transition for state q1 is obtained as: δ'([q1], 0) = [q1, q2] (new state generated) δ'([q1], 1) = [q1] 84 Mrs.D.Jena Catherine Bel, AP/CSE, VEC](https://image.slidesharecdn.com/fullunit1-220307085807/75/Theory-of-Computation-Unit-1-84-2048.jpg)
![Now we will obtain δ' transition on [q1, q2]. δ'([q1, q2], 0) = δ(q1, 0) ∪ δ(q2, 0) = {q1, q2} ∪ {q2} = [q1, q2] δ'([q1, q2], 1) = δ(q1, 1) ∪ δ(q2, 1) = {q1} ∪ {q1, q2} = {q1, q2} = [q1, q2] The state [q1, q2] is the final state as well because it contains a final state q2. 85 Mrs.D.Jena Catherine Bel, AP/CSE, VEC](https://image.slidesharecdn.com/fullunit1-220307085807/75/Theory-of-Computation-Unit-1-85-2048.jpg)
![State 0 1 →[q0] [q0] [q1] [q1] [q1, q2] [q1] *[q1, q2] [q1, q2] [q1, q2] The transition table for the constructed DFA will be: 86 Mrs.D.Jena Catherine Bel, AP/CSE, VEC](https://image.slidesharecdn.com/fullunit1-220307085807/75/Theory-of-Computation-Unit-1-86-2048.jpg)