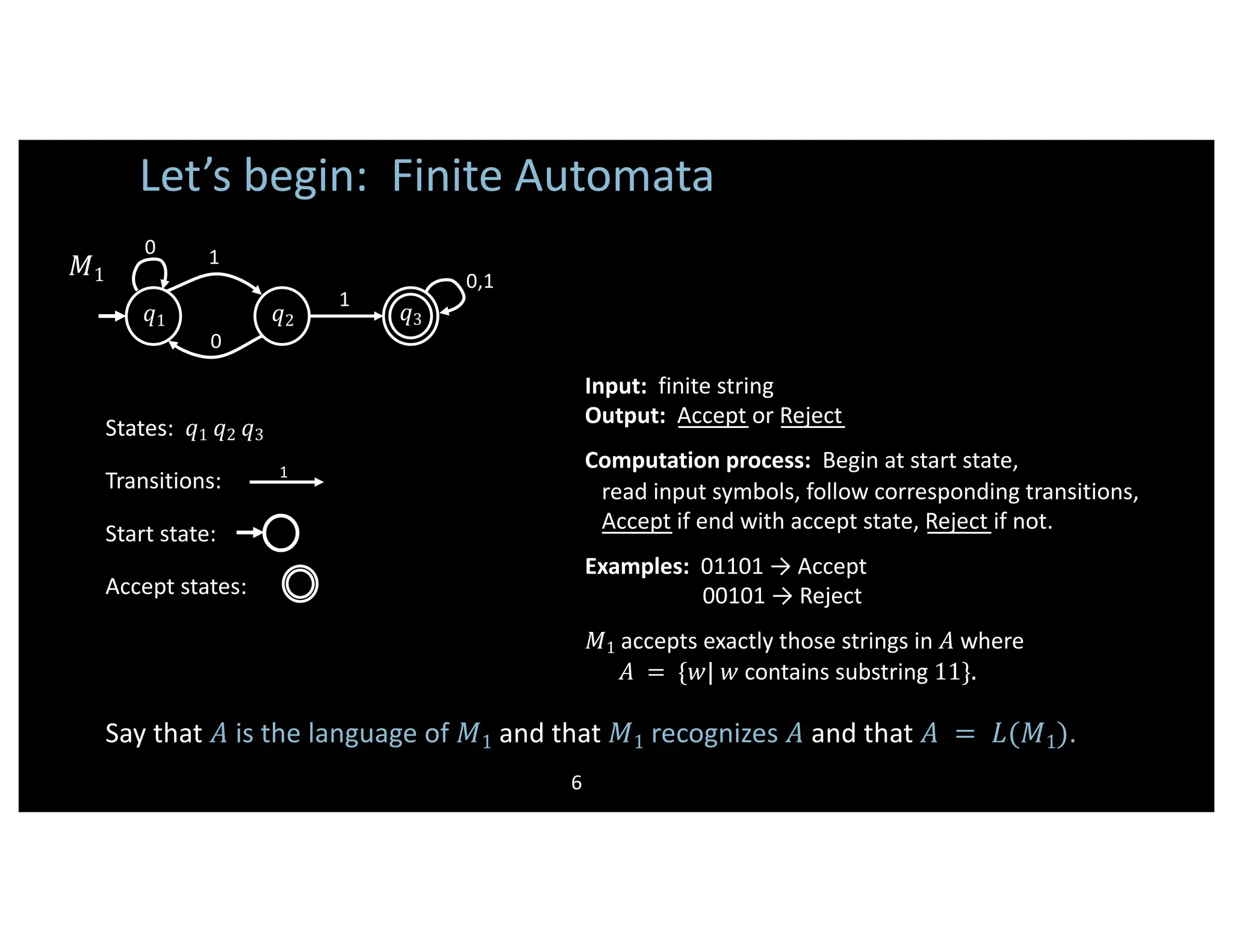
This document provides an overview of the 18.404/6.840 Intro to Theory of Computation course taught by Mike Sipser at MIT. The course covers computability theory from the 1930s-1950s, including models of computation like Turing machines and complexity theory from the 1960s to present, including the P vs NP problem. The course will include lectures, recitations, homework, midterms, and exams. Topics covered will include finite automata, regular languages/expressions, and proofs of closure properties for regular languages.







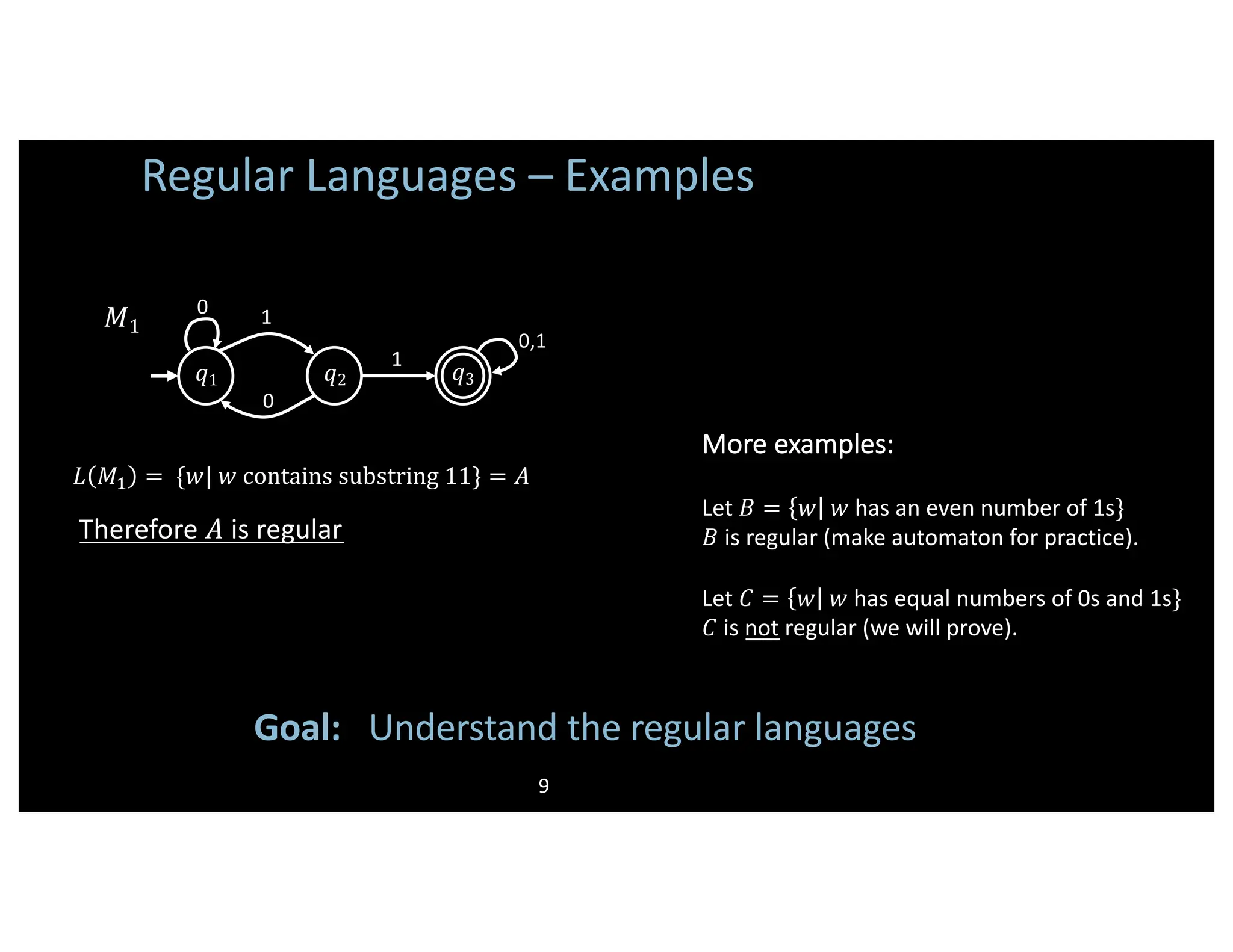
![Regular Expressions Regular operations. Let !, # be languages: - Union: ! ∪ # = & & ∈ ! or & ∈ #} - Concatenation: ! ∘ # = *+ * ∈ ! and + ∈ #} = !# - Star: !∗ = *- … */ each *0 ∈ ! for 1 ≥ 0} Note: ε ∈ !∗ always Example. Let ! = {good, bad} and # = {boy, girl}. - ! ∪ # = {good, bad, boy, girl} - ! ∘ # = !# = {goodboy, goodgirl, badboy, badgirl} - !∗ = {ε, good, bad, goodgood, goodbad, badgood, badbad, goodgoodgood, goodgoodbad, … } Regular expressions - Built from Σ, members Σ, ∅, ε [Atomic] - By using ∪,∘,∗ [Composite] Examples: - 0 ∪ 1 ∗ = Σ∗ gives all strings over Σ - Σ∗ 1 gives all strings that end with 1 - Σ∗ 11Σ∗ = all strings that contain 11 = : ;- Goal: Show finite automata equivalent to regular expressions 10](https://image.slidesharecdn.com/toc1-240310081949-b3491eb3/75/toc1-pdf-the-theory-of-computation-for-master-of-computer-applications-10-2048.jpg)
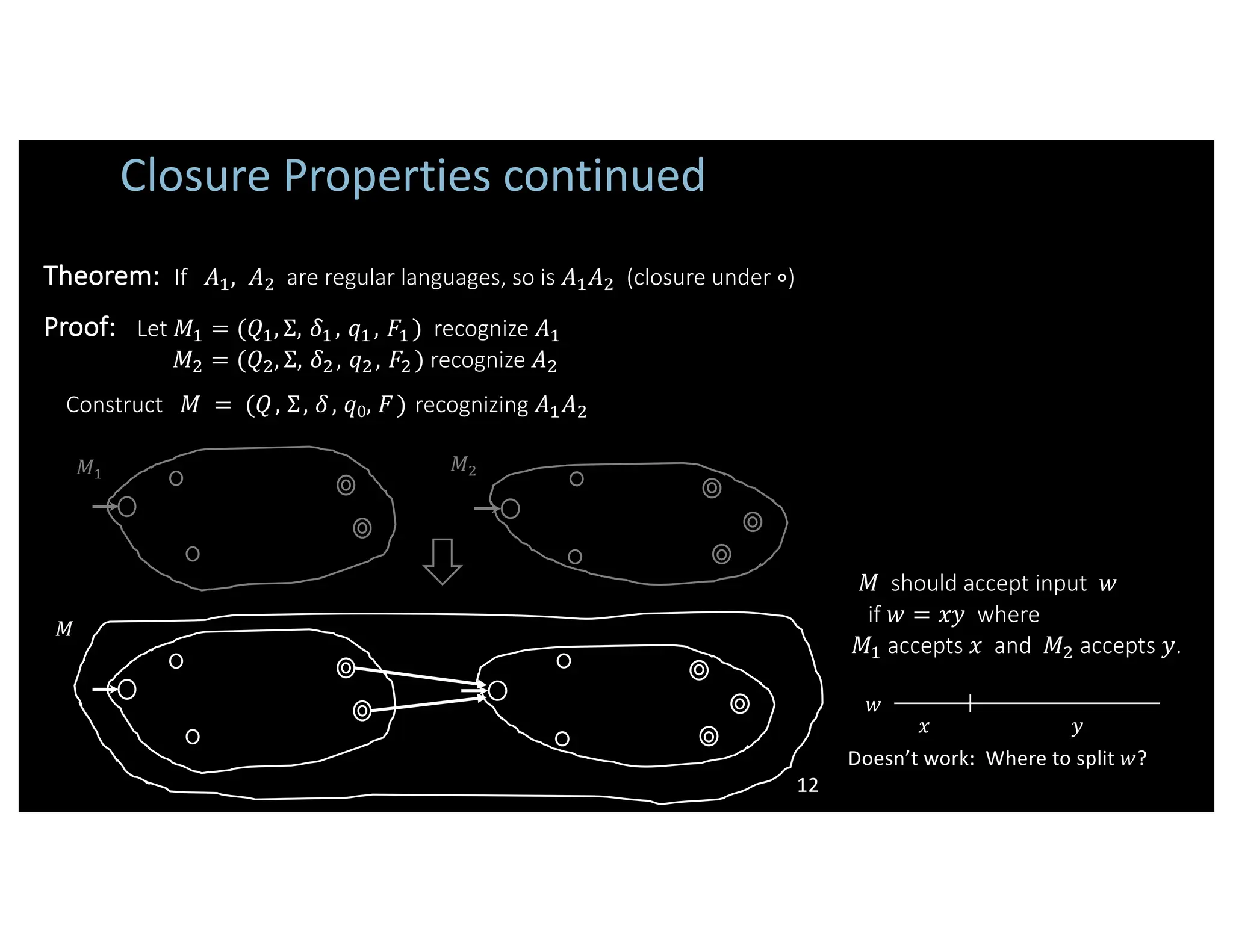
![&$ 1 &" , Closure Properties for Regular Languages Theorem: If !", !$ are regular languages, so is !" ∪ !$ (closure under ∪) Proof: Let &" = ()", Σ, +" , ," , -" ) recognize !" &$ = ()$, Σ, +$ , ,$ , -$ ) recognize !$ Construct & = (), Σ, +, ,0, -) recognizing !" ∪ !$ & should accept input 0 if either &" or &$ accept 0. Components of 2: Check-in 1.1 ) = )"×)$ In the proof, if &" and &$ are finite automata = ,", ,$ ," ∈ )" and ,$ ∈ )$} where &" has 8" states and &$ has 8$ states ,6 = (,", ,$) Then how many states does & have? (a) 8" + 8$ + ,, 1 , 7 = +" ,, 7 , +$ 1, 7 (b) 8" $ + 8$ $ - = -"×-$ NO! [gives intersection] (c) 8"×8$ - = -"×)$ ∪ )"×-$ Check-in 1.1 11](https://image.slidesharecdn.com/toc1-240310081949-b3491eb3/75/toc1-pdf-the-theory-of-computation-for-master-of-computer-applications-11-2048.jpg)