1
$\begingroup$

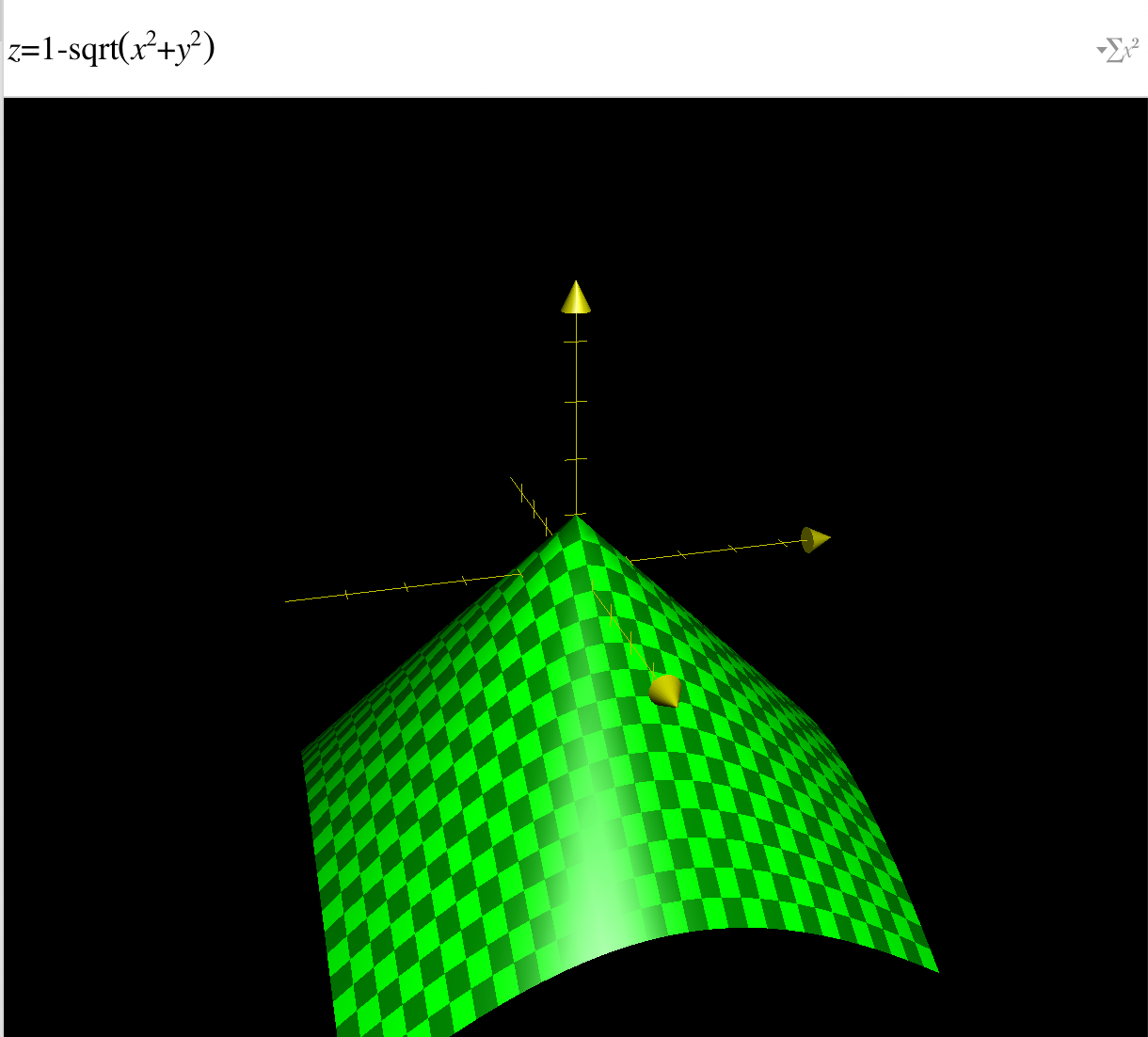
per this post, this formula

$Z = 1 - \sqrt{X^{2} + Y^{2}}$

generates a cone where the point is at (0, 0, 1) and it spreads out below that. It meets the x-y plane at the unit circle

enter image description here

I am trying to reproduce with Python

ax = plt.figure().gca(projection='3d') xx, yy = np.meshgrid(np.arange(-1,1.1,.1), np.arange(-1,1.1,.1)) zz = 1 - np.sqrt(xx**2, yy**2) ax.plot_surface(xx, yy, zz, alpha=.5)

and get this "roof"

enter image description here

each of xx, yy, zz is a 21 by 21 matrix, even if I increase them to 210 by 210, nothing changes, what am I missing?

Improve this question
$\endgroup$
3
  • $\begingroup$ Looks like your mesh is undersampled, in that it only has 6 vertices so its an approximate cone.. Can you increase the resolution some how ? $\endgroup$ Commented Oct 15, 2019 at 2:01
  • $\begingroup$ @PaulHK each of xx, yy, zz is a 21 by 21 matrix, even if I increase them to 210 by 210, nothing changes $\endgroup$ Commented Oct 15, 2019 at 2:13
  • $\begingroup$ What is np.sqrt(xx**2, yy**2)? I would expect something like np.sqrt(xx**2 + yy**2). Otherwise you're getting back an array of square roots, right? $\endgroup$ Commented Oct 15, 2019 at 2:21

1 Answer 1

Reset to default
2
$\begingroup$

You need to change the call to sqrt from:

np.sqrt(xx**2, yy**2)

to:

np.sqrt(xx**2 + yy**2)

Otherwise you're passing an array of values to the function and will be returned an array of values for the answer.

See here for details:

>>> np.sqrt([1,4,9])

array([ 1., 2., 3.])

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.