17
$\begingroup$

I'm trying to get into animation using Mathematica, and I want to create a simple animation where a sphere in a black space gets "morphed" into a cube. I know how to generate a cube and how to generate a sphere using Graphics3D:

Graphics3D[Sphere[]] Graphics3D[Cuboid[]]

But I'm not sure how to generate a "movie" of one morphing into another.

Improve this question
$\endgroup$
0

3 Answers 3

Reset to default
21
$\begingroup$

Slow, but it works:

Animate[ RegionPlot3D[ With[{u = Sin[t]^2*10 + 2}, Abs[x]^u + Abs[y]^u + Abs[z]^u < 1], {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, PerformanceGoal -> "Quality"], {t, 0, \[Pi]}]

enter image description here

Improve this answer
$\endgroup$
2
  • $\begingroup$ Can you explain how you got the formula? $\endgroup$ Commented Jun 7, 2018 at 15:08
  • 4
    $\begingroup$ @TreFox It's a fairly well-known formula in higher math. $\endgroup$ Commented Jun 7, 2018 at 15:24
17
$\begingroup$ 
reg = DiscretizeRegion[Cuboid[{-1, -1, -1}, {1, 1, 1}], MaxCellMeasure -> .01]; DynamicModule[{pts = MeshCoordinates[reg], norms = Norm /@ MeshCoordinates[reg]} , Animate[ Graphics3D@GraphicsComplex[ Dynamic[ pts /(1 - t + t norms) ], {EdgeForm@None, MeshCells[reg, {2}]} ] , {t, 0, 1}, AnimationRate -> 1, AnimationDirection -> ForwardBackward] ]

enter image description here

Improve this answer
$\endgroup$
2
  • $\begingroup$ Can you provide a short explanation of how you put this code together? $\endgroup$ Commented Jun 7, 2018 at 15:41
  • 2
    $\begingroup$ @TreFox cuboid -> cuboid's mesh -> coordinates + polygons. Then, normalized coordinates of this cuboid are on a sphere so I just scale the norm between 1 and original one. I'm encouraging your to take this code apart and experiment, see what's inside. $\endgroup$ Commented Jun 7, 2018 at 16:35
7
$\begingroup$

Updated

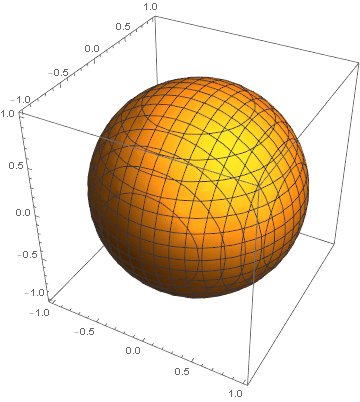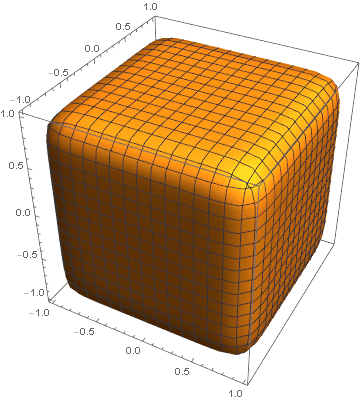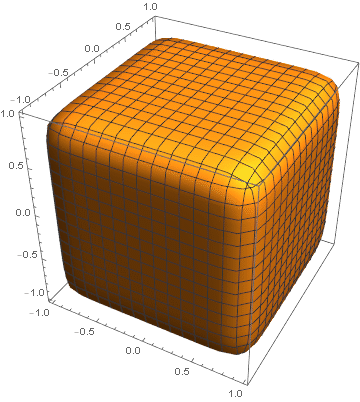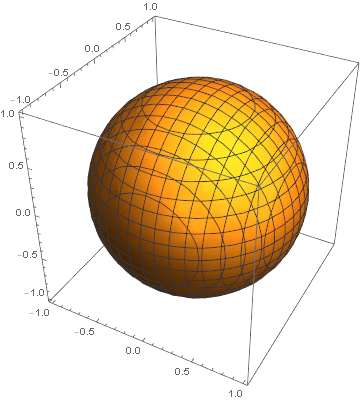
plt=ParametricPlot3D[{Cos[ϕ]*Sin[θ], Sin[θ]*Sin[ϕ], Cos[θ]}, {θ, 0, Pi}, {ϕ, 0, 2*Pi}, PlotPoints -> 200, PlotRange -> 1, ImageSize -> 400, Axes -> False, ColorFunction -> (Hue[#5, 1, 1, 0.75] &)]; cf = Compile[{{v, _Real, 1}, t}, (1 - t) v + t v/(Sqrt[2] Max[Abs[v]]), RuntimeAttributes -> {Listable}]; Manipulate[plt /. GraphicsComplex[pts_, rest___] :> GraphicsComplex[cf[pts, t], rest], {t, 0., 1}]

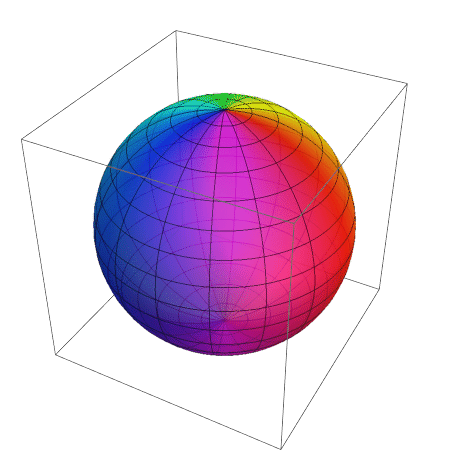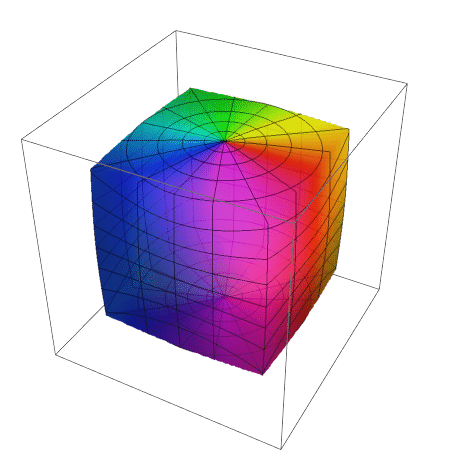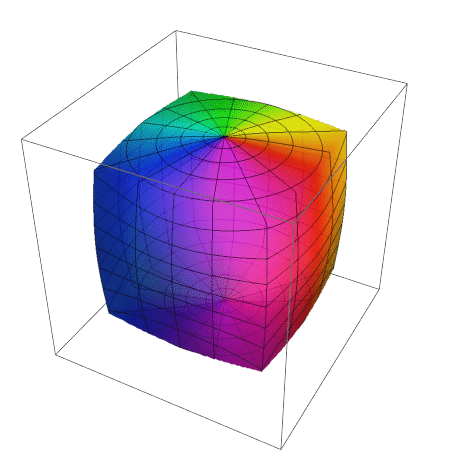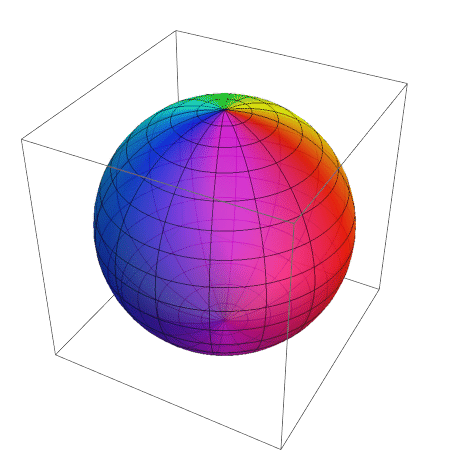
enter image description here

Previous answer:

Rectangle to circle:

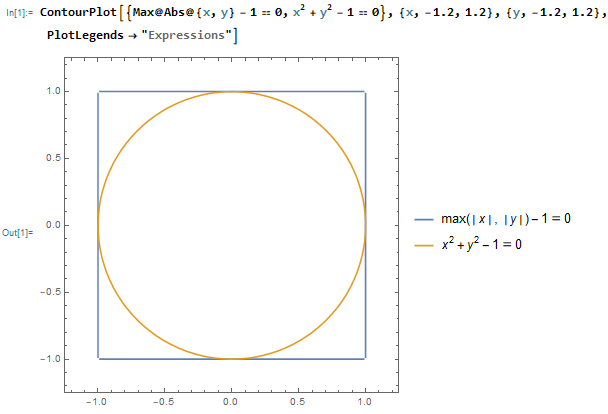
enter image description here

Manipulate[ ContourPlot[(1 - t) (Max@Abs@{x, y} - 1) + t (x^2 + y^2 - 1) == 0, {x, -1.2, 1.2}, {y, -1.2, 1.2}, PlotPoints -> 80], {t, 0, 1}]

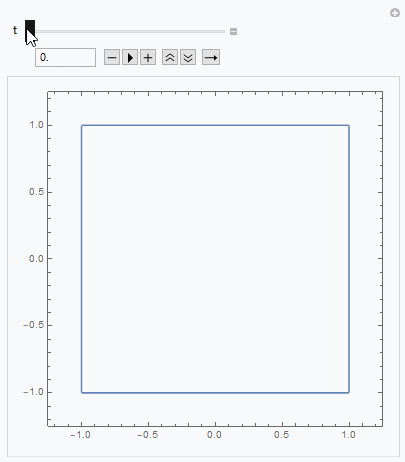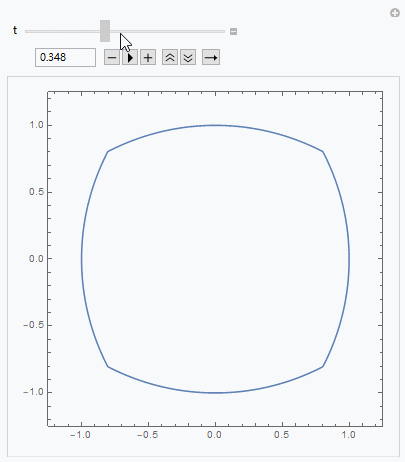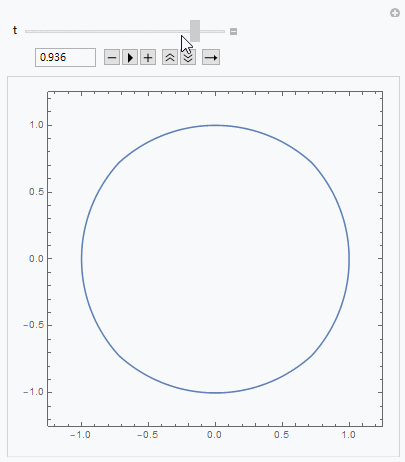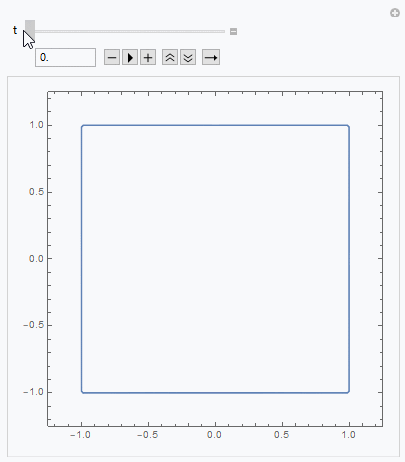
enter image description here

Cube to sphere:

frames = ParallelTable[ ContourPlot3D[(1 - t) (Max[Abs@{x, y, z}] - 1) + t (x^2 + y^2 + z^2 - 1) == 0, {x, -#, #}, {y, -#, #}, {z, -#, #}, PlotPoints -> 10, Mesh -> None, Boxed -> False, Axes -> False] &@1.1, {t, 0, 1, 1/50.}]; // AbsoluteTiming Animate[frames[[i]], {i, 1, Length[frames], 1}]

enter image description here

Improve this answer
$\endgroup$
2
  • $\begingroup$ what a beautiful answer! $\endgroup$ Commented May 2, 2022 at 3:17
  • $\begingroup$ @BlackMild Thanks for your appreciation. $\endgroup$ Commented May 4, 2022 at 11:40

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.