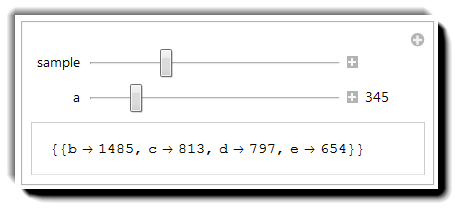
I tried to find a non-trivial integer solution to the equation
$$2012^2=a^2+b^2+c^2+d^2+e^2$$ with Mathematica but the computation takes minutes; I might be doing something wrong.
FindInstance[2012^2 == a^2 + b^2 + c^2 + d^2 + e^2 && a > 0 && b > 0 && c > 0 && d > 0 && e > 0, {a, b, c, d, e}, Integers] But when I try
FindInstance[2012^1 == a^2 + b^2 + c^2 + d^2 + e^2 && a > 0 && b > 0 && c > 0 && d > 0 && e > 0, {a, b, c, d, e}, Integers] I get an immediate result.