2
$\begingroup$

I want to solve a Laplace PDE in a polar coordinate system with finite difference method, but I have a problem with boundary conditions at r = 0.

Here is what I found on the Internet: http://homepages.see.leeds.ac.uk/~amt6xw/Distance%20Learning/CFD5030/node10.html

The formula for discretization is here: 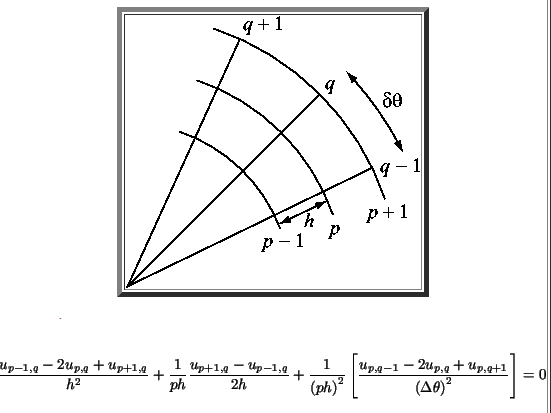enter image description here

I started off from a Cartesian coordinate system, from a rectangle grid. I tried to transfrom it into polar coordinates, but I don't know how to add/define the boundary conditions at r = 0, but in r = R = 0.

R = 0.04; n = 10; m = 10; Δr = R/n; Δθ = R/m; ϕ[n, j_] = 0;(*???*) ϕ[i_, m] = 0;(*???*) vars = Flatten[Table[ϕ[i, j], {i, 1, n - 1}, {j, 1, m - 1}]]; eqns = Flatten[Table[1/Δr^2 (1 - 1/(2 m)) ϕ[i - 1, j] - 2 ϕ[i, j] + (1 - 1/(2 m)) ϕ[i + 1, j] + 1/(m Δθ)^2 (ϕ[i, j + 1] - 2 ϕ[i, j] + ϕ[i, j - 1]) == 0, {i, 1, n - 1}, {j, 1, m - 1}]]; sol = Solve[eqns, vars][[1]]; ϕsol = Interpolation[ Flatten[Table[{i Δr, j Δθ, ϕ[i, j]}, {i, 0, n}, {j, 0, m}] /. sol, 1]];

When I solve analitycal the result is here: 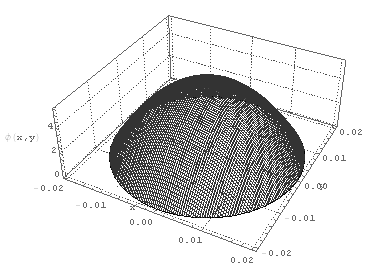enter image description here

But I don't know how to solve numerically

Improve this question
$\endgroup$
4
  • $\begingroup$ A previous version of this question was closed. To avoid the same fate with this version of the question, you should show what your specific issue in Mathematica is and how you have so far tried to address it. $\endgroup$ Commented Mar 30, 2015 at 16:47
  • $\begingroup$ @Jens I corrected the question $\endgroup$ Commented Mar 30, 2015 at 18:08
  • 1
    $\begingroup$ I think you are looking for the last equation on the slide you shared. $\endgroup$ Commented Mar 30, 2015 at 18:32
  • 1
    $\begingroup$ This PDF shows what to do at $r=0$ to avoid blow up, which is to set one of the constant of integrations to zero. May be you can follow this derivation and apply your numerical solution to the resulting solution. $\endgroup$ Commented Mar 31, 2015 at 14:20

1 Answer 1

Reset to default
2
$\begingroup$

OK, let me kill this unanswered question. As already pointed out in the comment above, one possible treatment for $\nabla^2 U$ at $r=0$ is

$$\nabla^2 U = \frac{4 \left( u_m - u_0 \right)}{\left( \Delta r \right)^2}$$

where $u_m$ is the mean value of $u$ along $r = \Delta r$. Aside from this, there're dozens of simple mistakes in the original code sample and I'd like not to point out them one by one. The last illustration isn't correct either, it's probably a solution of Possion equation (To be more specific, the equation in another question of OP, I guess ). Anyway, the following is the fixed code. The b.c. chosen here is $ϕ(R, θ) = \sin(2 \pi θ)$.

Clear[ϕ] R = 4/100; n = 25; m = 25; Δr = R/n; Δθ = 2 Pi/m; ϕ[0, j_] = ϕ[0, 0]; ϕ[n, j_] = Sin[2 Pi j/m]; ϕ[i_, j_?(! 0 <= # < m &)] = ϕ[i, Mod[j, m]]; vars = Union@Flatten[Table[ϕ[i, j], {i, 0, n - 1}, {j, 0, m}]]; eqns = Flatten@ Table[((ϕ[i - 1, j] - 2 ϕ[i, j] + ϕ[i + 1, j])/Δr^2 + 1/(i Δr) (ϕ[i + 1, j] - ϕ[i - 1, j])/(2 Δr) + 1/(i Δr)^2 (ϕ[i, j + 1] - 2 ϕ[i, j] + ϕ[i, j - 1])/ (Δθ^2)) == 0, {i, 1, n - 1}, {j, 1, m}]; eqadditional = With[{ϕm = Mean@Table[ϕ[1, j], {j, 1, m}]}, (4 (ϕm - ϕ[0, 0]))/Δr^2 == 0]; solrule = NSolve[Flatten@{eqns, eqadditional}, vars][[1]]; solcoord = solrule /. (_[i_, j_] -> val_) :> {i Δr Cos[j Δθ], i Δr Sin[j Δθ], val}; bccoord = Table[{n Δr Cos[j Δθ], n Δr Sin[j Δθ], N@ϕ[n, j]}, {j, 1, m}]; ListPointPlot3D[solcoord~Join~bccoord]

Mathematica graphics

Notice you can select the formula and press Ctrl+Shift+T to make it more readable.

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.