2
$\begingroup$

Consider the following Laplace equation and boundary condition $$\begin{equation}\begin{cases} \Delta \theta(r,\phi)=0 \\ \int d \vec{\ell}\cdot\nabla \theta(r,\phi)=2\pi \end{cases} \end{equation}$$ where $\phi\in[0,2\pi)$, $r\in[0,\infty)$ and the integral is over a circular contour of constant $r$ around the origin such that $d\vec{\ell}=rd\phi \hat{\phi}$ with $\hat{\phi}$ a unit vector in direction $\phi$. The solution to this equation is simply $\theta(r,\phi)=\phi$.

I want to learn how to solve this equation numerically in Mathematica and (approximately) recreate the solution in Cartesian coordinates. To this end, I'm taking a cylindrical domain with an annulus to avoid problems at $r=0$. The outer radius is $R_{1}=1$ and the inner radius is $R_{0}=0.1$. The domain looks like this

enter image description here

Following Solve Laplace equation in Cylindrical - Polar Coordinates, I seem to get the correct solution in polar coordinates but not in Cartesian coordinates and I don't understand why.

Any help is appreciated.

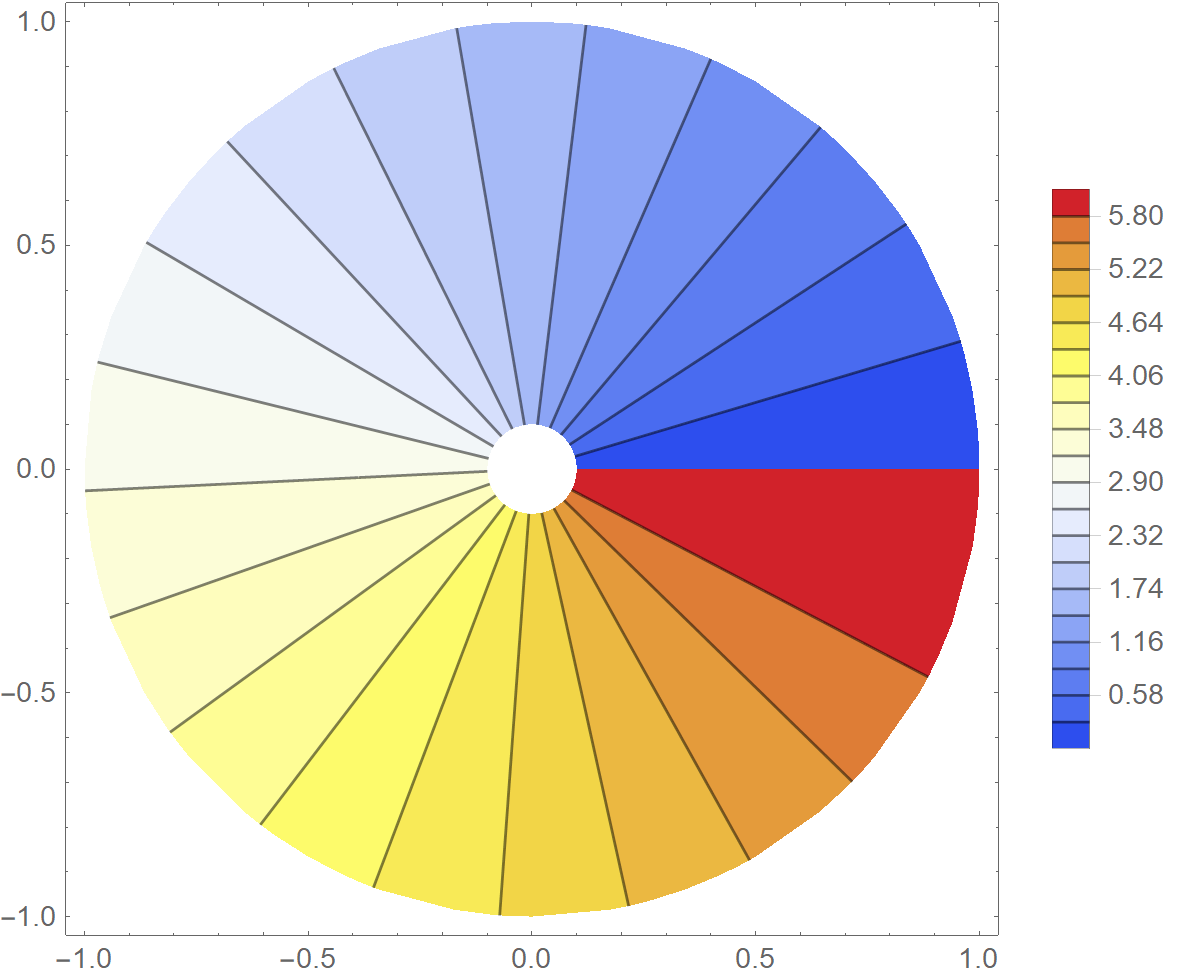
In Polar coordinates I get

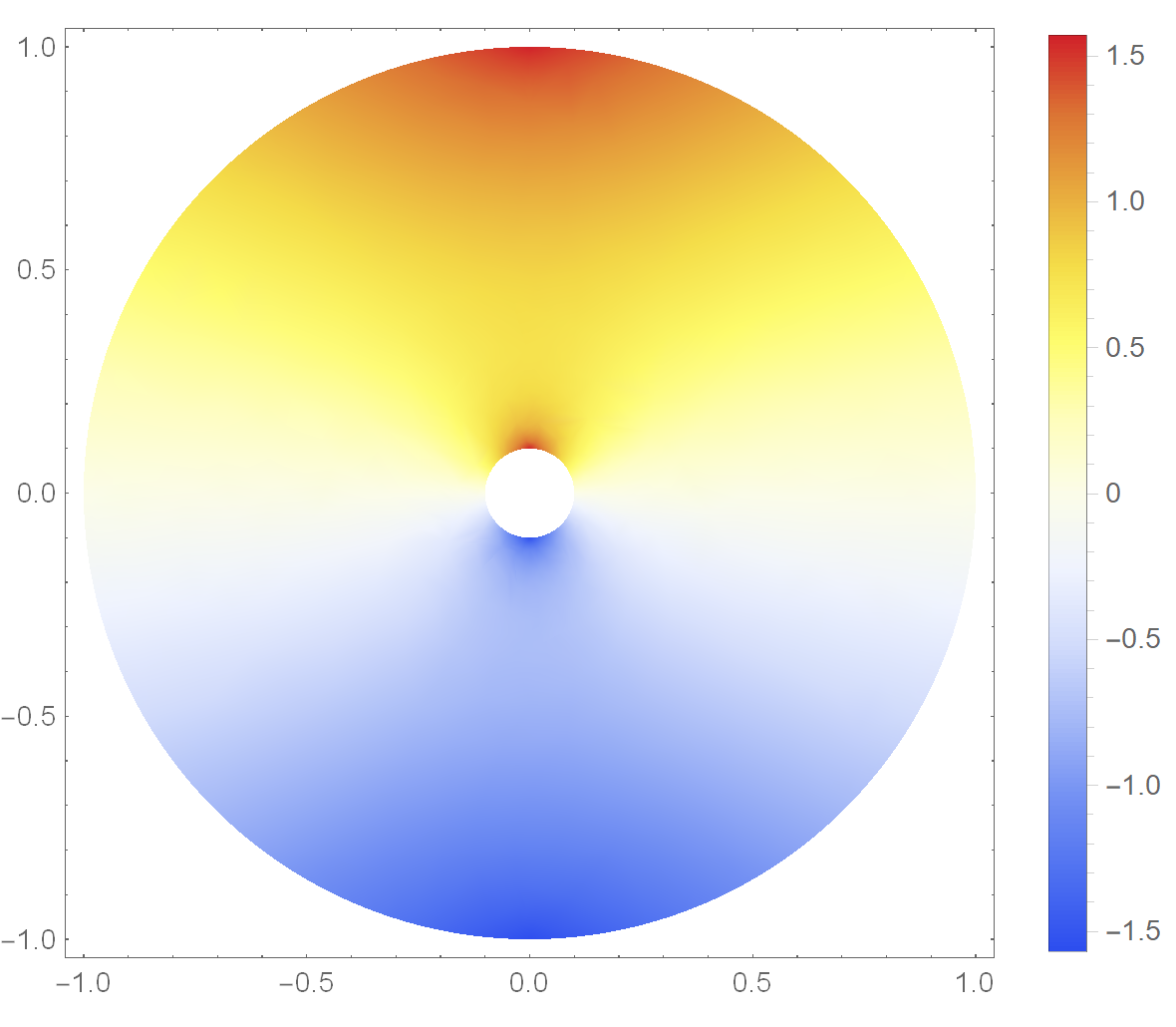
enter image description here

and in Cartesian coordinates I get

enter image description here

This is the code in polar coordinates

R1 = 1; R0 = 0.1; regionCyl = DiscretizeRegion[ RegionDifference[ ImplicitRegion[ 0 <= r <= R1 && 0 <= \[Phi] <= 2 \[Pi], {r, \[Phi]}], ImplicitRegion[ 0 <= r <= R0 && 0 <= \[Phi] <= 2 \[Pi], {r, \[Phi]}]], PrecisionGoal -> 6]; laplacianCil = Laplacian[\[Theta][r, \[Phi]], {r, \[Phi]}, "Polar"]; boundaryConditionCil = {DirichletCondition[\[Theta][ r, \[Phi]] == \[Phi], {r == R0, 0 <= \[Phi] <= 2 \[Pi]}], DirichletCondition[\[Theta][r, \[Phi]] == \[Phi], {r == R1, 0 <= \[Phi] <= 2 \[Pi]}]}; solCyl = NDSolveValue[{laplacianCil == 0, boundaryConditionCil}, \[Theta], {r, \[Phi]} \[Element] regionCyl, MaxSteps -> Infinity]; potentialSquareRepresentation = ContourPlot[ solCyl[r, \[Phi]], {r, \[Phi]} \[Element] solCyl["ElementMesh"], ColorFunction -> "Temperature", Contours -> 20, PlotLegends -> Automatic]; potentialCylindricalRepresentation = Show[potentialSquareRepresentation /. GraphicsComplex[array1_, rest___] :> GraphicsComplex[(#[[1]] {Cos[#[[2]]], Sin[#[[2]]]}) & /@ array1, rest], PlotRange -> Automatic]

and this is the code in Cartesian coordinates 

R1 = 1; R0 = 0.1; regionCyl = DiscretizeRegion[ RegionDifference[ImplicitRegion[Sqrt[x^2 + y^2] <= R1, {x, y}], ImplicitRegion[Sqrt[x^2 + y^2] <= R0, {x, y}]], PrecisionGoal -> 7]; laplacian = Laplacian[\[Theta][x, y], {x, y}]; boundaryCondition = {DirichletCondition[\[Theta][x, y] == ArcSin[y/Sqrt[x^2 + y^2]], {Sqrt[x^2 + y^2] == R0, 0 <= y/Sqrt[x^2 + y^2] <= 2 \[Pi]}], DirichletCondition[\[Theta][x, y] == ArcSin[y/Sqrt[x^2 + y^2]], {Sqrt[x^2 + y^2] == R1, 0 <= y/Sqrt[x^2 + y^2] <= 2 \[Pi]}]}; sol = NDSolveValue[{laplacian == 0, boundaryCondition}, \[Theta], {x, y} \[Element] regionCyl, MaxSteps -> Infinity]; DensityPlot[sol[x, y], {x, y} \[Element] regionCyl, ColorFunction -> "TemperatureMap", PlotLegends -> Automatic, ImageSize -> Medium]
Improve this question
$\endgroup$
2
  • 1
    $\begingroup$ It's not about the solution NDSolveValue being incorrect (I haven't checked but it lookes plausible to me.) The problem is that the pde you gave cannot be interpreted as a pde on the annulus: The boundary condition forbids that. In fact, $(r,\varphi) \mapsto \varphi$ is not a harmonic function on the annulus, in particular, because it must have a jump. $\endgroup$ Commented Feb 13, 2019 at 13:35
  • $\begingroup$ @HenrikSchumacher Then I don't understand why the solution in polar coordinates does agree with the analytical solution (in an infinite domain). How would you model this problem numerically? $\endgroup$ Commented Feb 13, 2019 at 13:52

1 Answer 1

Reset to default
8
$\begingroup$

In Cartesian coordinates, the solution $\theta $ has a gap on the line $y=0$.To get a solution, you need to make a cut and define a solution on both sides of the cut, for example:

R1 = 1; y0 = 0.01; regionCyl = DiscretizeRegion[ RegionDifference[ImplicitRegion[Sqrt[x^2 + y^2] <= R1, {x, y}], ImplicitRegion[-R1 <= x <= 0 && -y0 <= y <= y0, {x, y}]]]; laplacian = Laplacian[\[Theta][x, y], {x, y}]; boundaryCondition = {DirichletCondition[\[Theta][x, y] == ArcTan[x, y], x^2 + y^2 == R1^2], DirichletCondition[\[Theta][x, y] == Pi, y == y0], DirichletCondition[\[Theta][x, y] == -Pi, y == -y0]}; sol = NDSolveValue[{laplacian == 0, boundaryCondition}, \[Theta], {x, y} \[Element] regionCyl, Method -> {"FiniteElement", "InterpolationOrder" -> {\[Theta] -> 2}, "MeshOptions" -> {"MaxCellMeasure" -> 0.0001}}]; {DensityPlot[sol[x, y], {x, y} \[Element] regionCyl, ColorFunction -> "TemperatureMap", PlotLegends -> Automatic, ImageSize -> Medium], ContourPlot[sol[x, y], {x, y} \[Element] regionCyl, ColorFunction -> "TemperatureMap", PlotLegends -> Automatic, ImageSize -> Medium, Contours -> 20]}

fig1

Improve this answer
$\endgroup$
7
  • $\begingroup$ I see your point. Thanks @Alex Trounev $\endgroup$ Commented Feb 14, 2019 at 12:18
  • $\begingroup$ @AsafMiron You're welcome! $\endgroup$ Commented Feb 14, 2019 at 12:22
  • $\begingroup$ just wondering, is it straightforward to generalize this solution if instead of the Laplace equation theta I have two coupled nonlinear PDE for theta and another field? $\endgroup$ Commented Feb 17, 2019 at 18:44
  • $\begingroup$ Does this other field depend on theta and also have a gap? $\endgroup$ Commented Feb 17, 2019 at 19:46
  • $\begingroup$ Both fields are coupled by non-linear equations and depend on both x and y. I'm interested in boundary conditions that, similarly to my original post, are equal to $\phi$ along a circle centered around $x=x_{0},y=0$ and $-\phi$ along a circle centered around $x=-x_{0},y=0$. Thus, there is a gap along the interval $[-x_{0},x_{0}]$. Both circles have radius $R_{0}$ which is much smaller than $R_{1}$, the large outer circle radius. $\endgroup$ Commented Feb 18, 2019 at 7:43

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.