3
$\begingroup$

I have discrete optical spectra data consisting of pairs of wavelengths and intensities, and I would like to make a ListPlot in which the points are both joined, and colored according to the wavelength as is the filling.

Here is an example.

Here's fake data that illustrates the problem:

ListPlot[ Table[Style[{λ, Sin[λ/400]}, ColorData["VisibleSpectrum"][λ]], {λ, 400, 700, 5}], PlotStyle -> PointSize[Medium], Filling -> Axis, FillingStyle -> Function[{λ, y}, ColorData["VisibleSpectrum"][#[[1]] &]]]

I can get the points to be properly colored, but not the filling. Moreover, the ideal is to have a continuous filling underneath curve (as in the linked example), i.e., not discrete bars. I've tried numerous variations on the FillingStyle, without success.

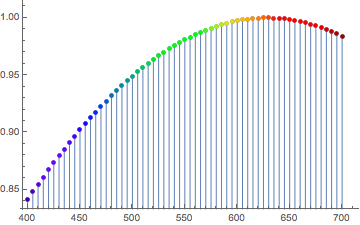
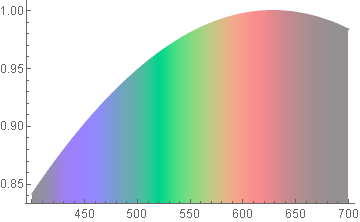
enter image description here

Improve this question
$\endgroup$
3
  • 2
    $\begingroup$ You might want to use the color functions here instead of ColorData["VisibleSpectrum"]. $\endgroup$ Commented Apr 18, 2017 at 1:28
  • $\begingroup$ But VisibleSpectrum takes the wavelength (in nanometers) and renders the color—just as is the form of my data. Shouldn't there be an easy way to call VisibleSpectrum in FillingStyle?! $\endgroup$ Commented Apr 18, 2017 at 1:32
  • 3
    $\begingroup$ My point in making my earlier comment was that "VisibleSpectrum" does not always give accurate colors. It was only a suggestion; if you insist on using "VisibleSpectrum", then sure, you can use it in FillingStyle: ListLinePlot[Table[{x, Sin[x/400]}, {x, 400, 700, 5}], ColorFunction -> (ColorData["VisibleSpectrum", #] &), ColorFunctionScaling -> False, Filling -> Axis] $\endgroup$ Commented Apr 18, 2017 at 1:34

3 Answers 3

Reset to default
5
$\begingroup$ 
fcolor = ColorData["VisibleSpectrum"]; ListPlot[Table[{x, Sin[x/400]}, {x, 400, 700, 5}], Joined -> True, ColorFunction -> Function[{x, y}, fcolor[x]], ColorFunctionScaling -> False, Filling -> Axis]

enter image description here

Improve this answer
$\endgroup$
4
  • $\begingroup$ Almost. I had found such a ColorFunction but 1) the color should be a function of the abscissa ($x$) value (not $y$ value) and 2) it should be colored according to ColorData["VisibleSpectrum"] (not Hue). Any way to fix that in your code? (I couldn't find it.) $\endgroup$ Commented Apr 18, 2017 at 1:22
  • $\begingroup$ Though now I see that JM in the comments has beat me to it... $\endgroup$ Commented Apr 18, 2017 at 1:48
  • $\begingroup$ @bill, I upvoted, don't fret. ;) I didn't answer because I was expecting you'd fix yours. $\endgroup$ Commented Apr 18, 2017 at 1:48
  • $\begingroup$ J.M.: You deserve the "win." Post and I'll accept it. Otherwise, I'll go with bill s. Regardless: Thanks you two! $\endgroup$ Commented Apr 18, 2017 at 1:49
5
$\begingroup$

If you really want to use "VisibleSpectrum" it can be supplied directly in Blend:

ListLinePlot[ Table[{x, Sin[x/400]}, {x, 400, 700, 5}] , ColorFunction -> (Blend["VisibleSpectrum", #] &) , ColorFunctionScaling -> False , Filling -> Axis ]

enter image description here

However I recommend that you do not use that inaccurate function but instead:

ChromaticityPlot; (* pre-load internals *) newVisibleSpectrum = With[ {colors = {Image`ColorOperationsDump`$wavelengths, XYZColor @@@ Image`ColorOperationsDump`tris}\[Transpose]}, Blend[colors, #] & ]; ListLinePlot[ Table[{x, Sin[x/400]}, {x, 400, 700, 5}] , ColorFunction -> newVisibleSpectrum , ColorFunctionScaling -> False , Filling -> Axis ]

enter image description here

See: A better "VisibleSpectrum" function?

Or with newVSgray also from there:

enter image description here

That provides the closest unclipped representation possible within sRGB.

Improve this answer
$\endgroup$
1
$\begingroup$

You can also use Interpolation

data = Table[{λ, Sin[λ/400]}, {λ, 400, 700, 5}]; f = Interpolation[data]; Plot[f[λ], {λ, 400, 700}, ColorFunction -> Function[{x, y}, ColorData["VisibleSpectrum"][x]], ColorFunctionScaling -> False, Filling -> Axis, FillingStyle -> Automatic, Axes -> False, Frame -> {{True, False}, {True, False}}, FrameLabel -> (Style[#, 14, Bold] & /@ {"Wavelength (nm)", "Intensity"})]

enter image description here

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.