4
$\begingroup$

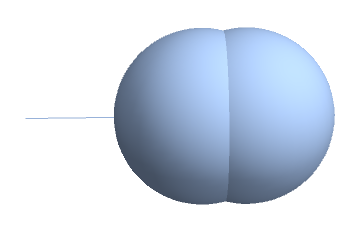
Whenever I try to find the intersection between a two regions, one of which is a derived region using RegionUnion, I get a BooleanRegion with which I can do little. 

s1 = Sphere[{0, 0, 0}, 0.1]; s2 = RegionUnion[Sphere[{0, 0, 0}, 0.1], Sphere[{0.05, 0, 0}, 0.1]]; l = Line[{{-0.2, 0, 0}, {0.01, 0, 0}}]; Show[Region[s2], Region[Line[{{-0.2, 0, 0}, {0.01, 0, 0}}]]]

enter image description here

RegionIntersection[s2, l]

BooleanRegion[(#1 || #2) && #3 &, {Sphere[{0, 0, 0}, 0.1], Sphere[{0.05, 0, 0}, 0.1], Line[{{-0.2, 0, 0}, {0.01, 0, 0}}]}]

RegionIntersection[s1, l]

Point[{{-0.1, 0, 0}}]

I am sure this has been answered somewhere else, or that I am missing something basic, but I can not find a reference

Improve this question
$\endgroup$

1 Answer 1

Reset to default
4
$\begingroup$

I agree that at the present time RegionIntersection can produce simplifications where the equivalent BooleanRegion version does not. Here is a function that converts a BooleanRegion object into an equivalent RegionUnion/RegionIntersection construct so that these additional simplifications have a chance to fire:

simplifyRegion[BooleanRegion[predicate_, regions_]] := With[ {dnf = BooleanConvert[predicate] /. {Or->RegionUnion, And->RegionIntersection}}, dnf @@ regions ]

Using BooleanConvert produces a boolean predicate in DNF form, which means that RegionIntersection fires before RegionUnion. Here is the output of simplifyRegion on your example:

RegionIntersection[s2,l] simplifyRegion @ %

BooleanRegion[(#1 || #2) && #3 &, {Sphere[{0, 0, 0}, 0.1], Sphere[{0.05, 0, 0}, 0.1], Line[{{-0.2, 0, 0}, {0.01, 0, 0}}]}]

BooleanRegion[#1 || #2 &, {Point[{{-0.1, 0, 0}}], Point[{{-0.05, 0, 0}}]}]

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.