1
$\begingroup$

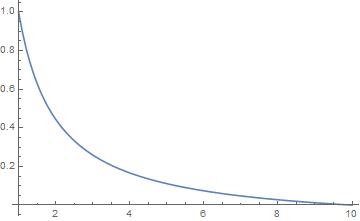
I was trying to solve Laplace's equation for a spherical capacitor, which is not difficult by hand, just to figure out the commands so I can eventually try something more complicated. Then, I ran into trouble.

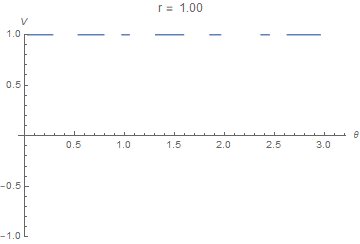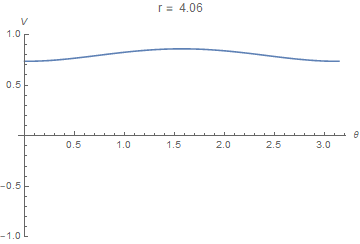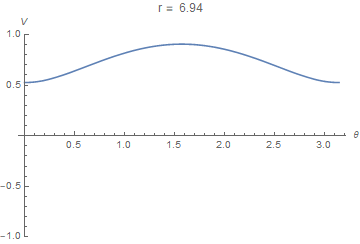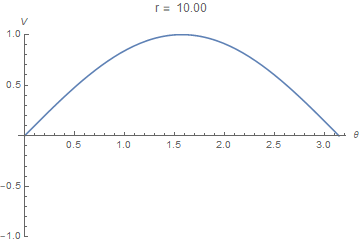
I tried to use spherical coordinates, and I got an error of a non real answer, or sometimes null.

leqn = ( Laplacian[V[r,\[Theta],\[Phi]],{r,\[Theta],\[Phi]},"Spherical" ] ==0 //Simplify) a=1; b=10; NDSolveValue[{leqn,V[a,\[Theta],\[Phi]]==1,V[b,\[Theta],\[Phi]]==0},V,{r,a,b},{\[Theta],0,\[Pi]},{\[Phi],0,2*\[Pi]}]

So I figured I'd try in Cartesian coordinates in order to figure out my error; it worked:

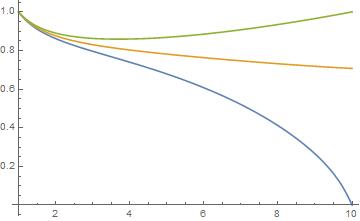
a=1;b=5 NDSolveValue[{Laplacian[u[x,y],{x,y}] == 0, DirichletCondition[u[x,y] == 1,Sqrt[x^2+y^2] ==a ], DirichletCondition[u[x,y] == 0,Sqrt[x^2+y^2] ==b] }, u, {x, y} \[Element]Annulus[{0,0},{a,b}]] Plot3D[%[x, y], {x, y} \[Element] Annulus[{0,0},{a,b}]]

But then if I try to be a little more explicit about the boundary conditions it stops working:

a=1;b=5 NDSolveValue[{Laplacian[u[x,y],{x,y}]== 0, u[x,y] == If[Norm[{x,y}]==a,1], DirichletCondition[u[x,y] == 0,Sqrt[x^2+y^2] ==b] }, u, {x, y} \[Element]Annulus[{0,0},{a,b}]] Plot3D[%[x, y], {x, y} \[Element] Annulus[{0,0},{a,b}]]

Anyway, I still can't figure out why the explicit form of the boundary condition didn't work.

Furthermore, I don't see why the polar version didn't work.

Improve this question
$\endgroup$
4
  • 2
    $\begingroup$ Your spherical coordinate code works for me v11.3. Even changing the bc's to functions of theta and phi works. You could try clearing the kernel unless your version is too old. $\endgroup$ Commented Mar 29, 2019 at 6:25
  • $\begingroup$ @BillWatts I tried both on the Wolfram programing cloud, and in Mathematica version "10.4.0 for Microsoft Windows (64-bit) (February 26, 2016)". I tried restarting the kernel. It still didn't work $\endgroup$ Commented Mar 29, 2019 at 18:48
  • $\begingroup$ @BillWatts 10.4.0 gave me the following error for my spherical coordinate code: NDSolveValue::femcnmd: "The PDE coefficient {{r,0,0},{0,1/r,0},{0,0,Csc[[Theta]]^2/r}} does not evaluate to a numeric matrix of dimensions {3,3} at the coordinate {1.,0.,0.`}" $\endgroup$ Commented Mar 29, 2019 at 18:54
  • $\begingroup$ @BillWatts "11.3.0 for Linux x86 (64-bit) (March 7, 2018)" in the cloud just gives up and it looks like the kernel quits $\endgroup$ Commented Mar 29, 2019 at 19:19

1 Answer 1

Reset to default
1
$\begingroup$

This is what I get.

leqn = (Laplacian[V[r, θ, ϕ], {r, θ, ϕ}, "Spherical"] == 0 // Simplify) a = 1; b = 10; sol = NDSolveValue[{leqn, V[a, θ, ϕ] == 1, V[b, θ, ϕ] == 0}, V, {r, a, b}, {θ, 0, π}, {ϕ, 0, 2*π}] Plot[sol[r, 0, 0], {r, a, b}, PlotRange -> All]

enter image description here

Get a little fancier.

sol = NDSolveValue[{leqn, V[a, θ, ϕ] == 1, V[b, θ, ϕ] == Sin[θ]}, V, {r, a, b}, {θ, 0, π}, {ϕ, 0, 2*π}] Plot[{sol[r, 0, 0], sol[r, π/4, 0], sol[r, π/2, 0]}, {r, a, b}, PlotRange -> All]

enter image description here

gifs = Table[ Plot[sol[r, θ, π/2], {θ, 0, π}, PlotRange -> {-1, 1}, AxesLabel -> {θ, V}, PlotLabel -> "r = " <> ToString[PaddedForm[N[r], {3, 2}]]], {r, a, b, (b - a)/50}]; ListAnimate[gifs]

enter image description here

V11.3 windows 10.

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.