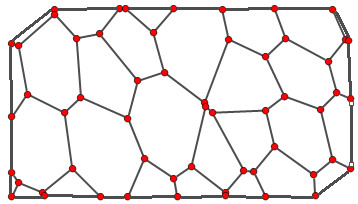
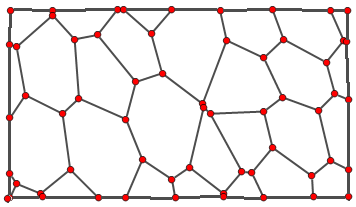
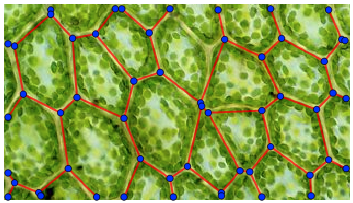
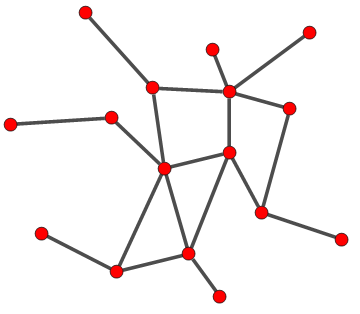
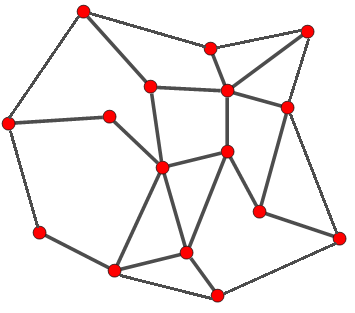
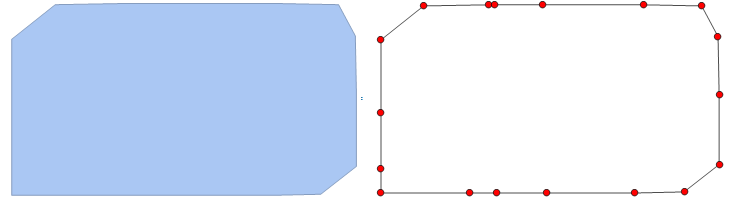
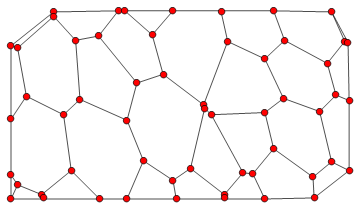
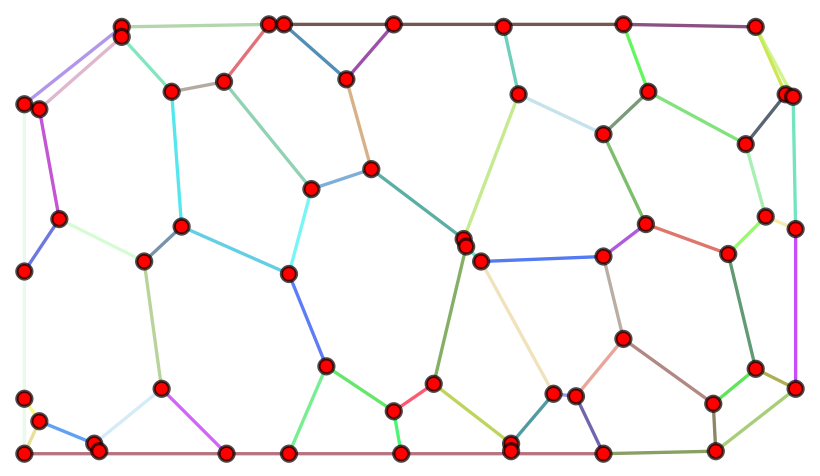
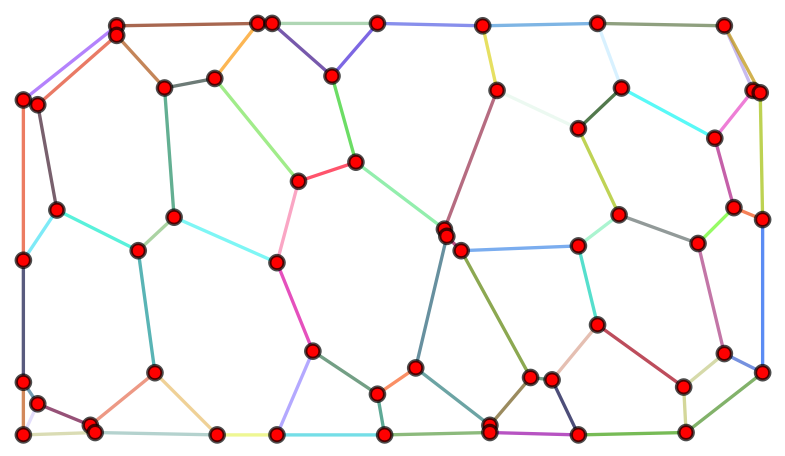
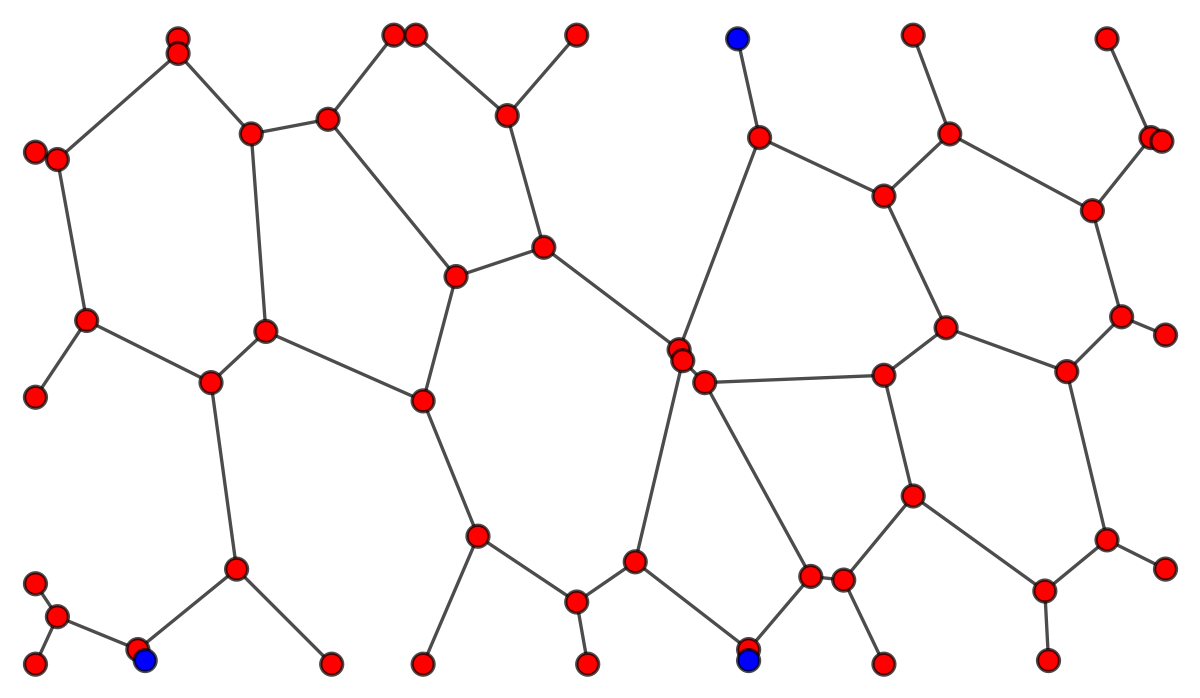
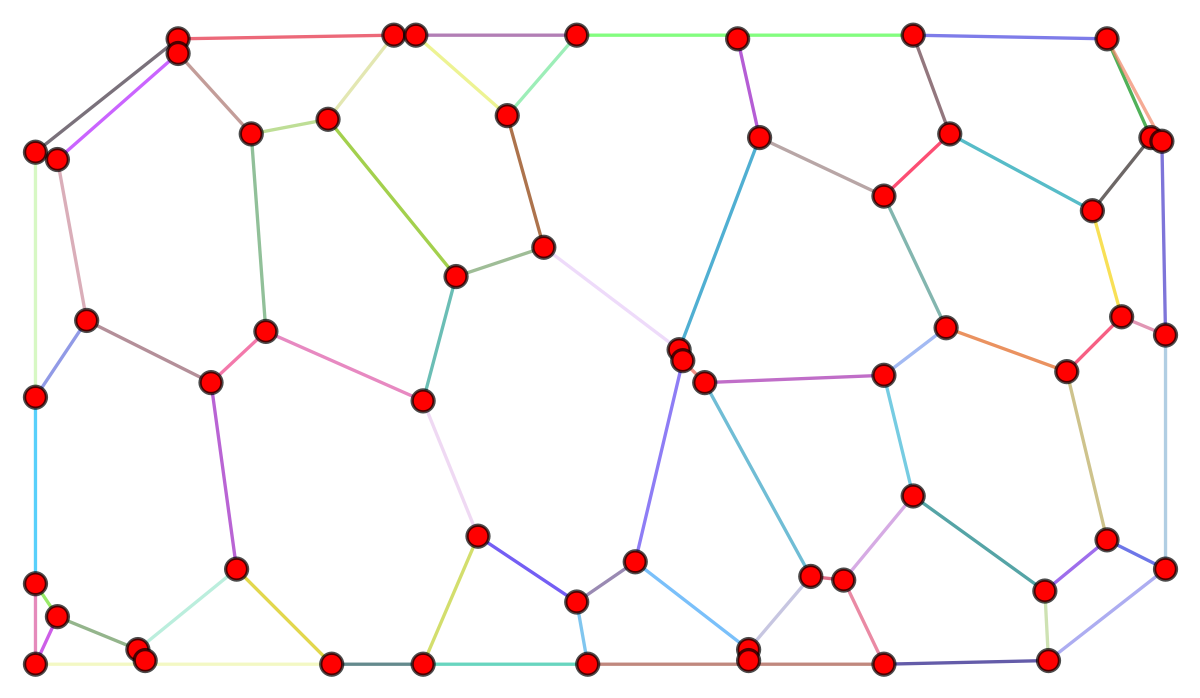
Consider the following graph g
I want to "close" it by adding the following edges
Alternatively, I would also be happy with something like
where I've added four "corner" vertices.
Now, this question is, in a way, a follow up to this answer, where I initially have a picture on which I draw a graph, as follows
Is it possible to turn the picture into a rectangle-shaped graph and then join them in somehow? This would lead to something like the second example.
Alternatively, I also thought about simply uniting 1-degree vertices that are close to each other, creating the first example graph.
In the end, I want a graph that defines a mesh, thus the need of "closing" the graph in this fashion. Ideally, I want KVertexConnectedGraphQ[g] = True for the closed graph.
Any ideas?
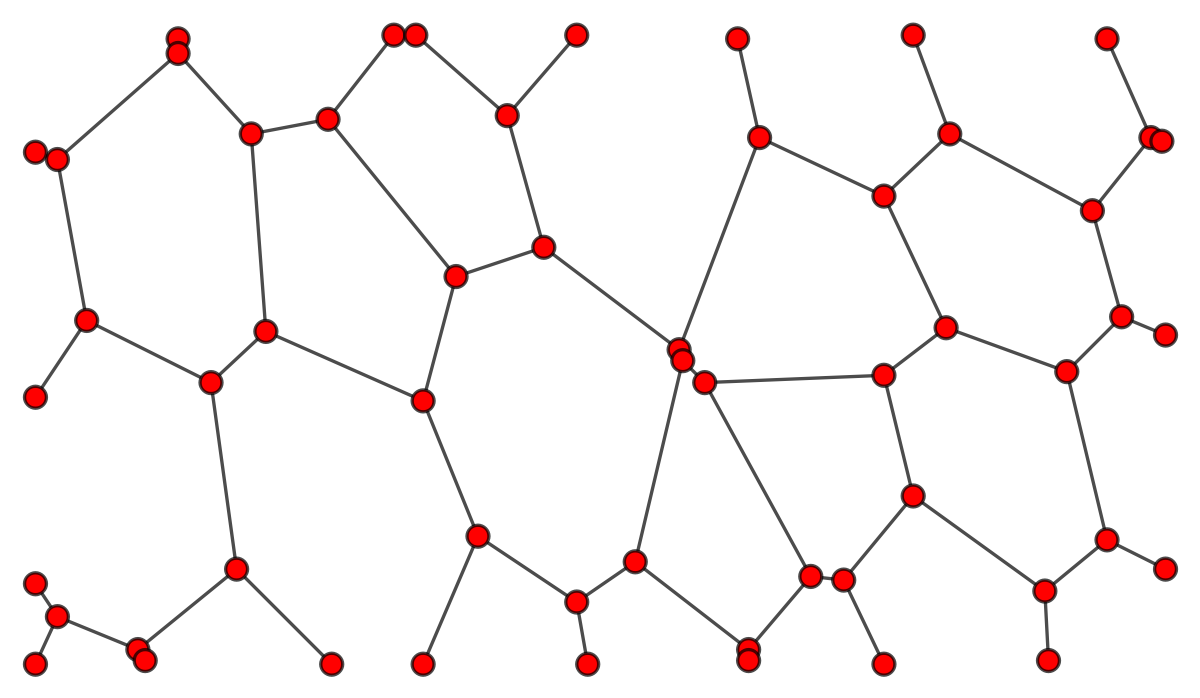
Edit 1: Note that my goal is to be able to do this for general graphs. For example, considering the graph
I want to get something like
I guess using something like ConvexHull (which doesn't correspond to what is drawn) in some matter could help my goal, but at this point I'm entirely sure how.
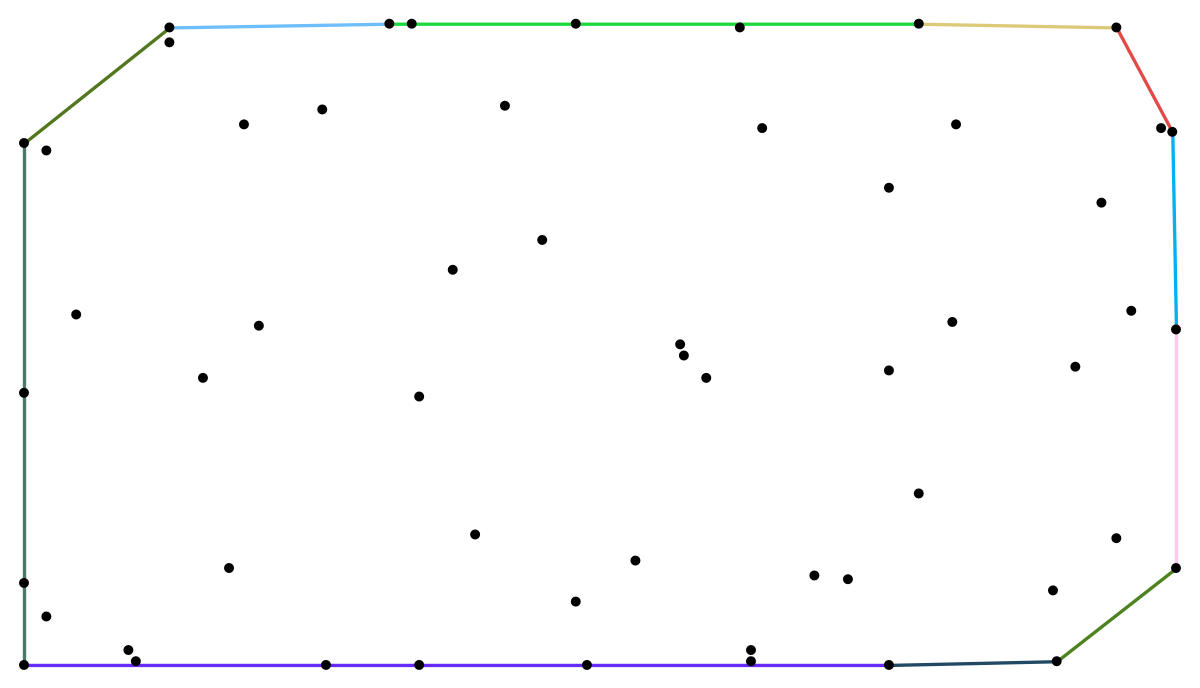
Edit 2: In order to be more practical consider the graph given by
g = Graph[{1 \[UndirectedEdge] 10, 2 \[UndirectedEdge] 9, 3 \[UndirectedEdge] 9, 4 \[UndirectedEdge] 12, 5 \[UndirectedEdge] 8, 6 \[UndirectedEdge] 13, 7 \[UndirectedEdge] 14, 8 \[UndirectedEdge] 11, 8 \[UndirectedEdge] 17, 9 \[UndirectedEdge] 20, 10 \[UndirectedEdge] 11, 10 \[UndirectedEdge] 21, 11 \[UndirectedEdge] 25, 12 \[UndirectedEdge] 18, 12 \[UndirectedEdge] 19, 13 \[UndirectedEdge] 18, 13 \[UndirectedEdge] 27, 14 \[UndirectedEdge] 15, 14 \[UndirectedEdge] 19, 16 \[UndirectedEdge] 17, 17 \[UndirectedEdge] 23, 18 \[UndirectedEdge] 24, 19 \[UndirectedEdge] 22, 20 \[UndirectedEdge] 21, 20 \[UndirectedEdge] 27, 21 \[UndirectedEdge] 34, 22 \[UndirectedEdge] 26, 22 \[UndirectedEdge] 29, 23 \[UndirectedEdge] 31, 23 \[UndirectedEdge] 33, 24 \[UndirectedEdge] 29, 24 \[UndirectedEdge] 30, 25 \[UndirectedEdge] 31, 25 \[UndirectedEdge] 34, 27 \[UndirectedEdge] 28, 28 \[UndirectedEdge] 32, 28 \[UndirectedEdge] 38, 29 \[UndirectedEdge] 37, 30 \[UndirectedEdge] 32, 30 \[UndirectedEdge] 35, 31 \[UndirectedEdge] 39, 32 \[UndirectedEdge] 41, 34 \[UndirectedEdge] 36, 35 \[UndirectedEdge] 42, 35 \[UndirectedEdge] 44, 36 \[UndirectedEdge] 45, 36 \[UndirectedEdge] 54, 37 \[UndirectedEdge] 40, 37 \[UndirectedEdge] 44, 38 \[UndirectedEdge] 45, 38 \[UndirectedEdge] 48, 39 \[UndirectedEdge] 47, 39 \[UndirectedEdge] 53, 41 \[UndirectedEdge] 42, 41 \[UndirectedEdge] 48, 42 \[UndirectedEdge] 56, 43 \[UndirectedEdge] 46, 44 \[UndirectedEdge] 51, 45 \[UndirectedEdge] 55, 46 \[UndirectedEdge] 47, 46 \[UndirectedEdge] 52, 47 \[UndirectedEdge] 49, 48 \[UndirectedEdge] 50}, VertexCoordinates -> {{102.5`, 175.5`}, {84.5`, 152.5`}, {108.5`, 175.5`}, {133.5`, 153.5`}, {152.5`, 175.5`}, {244.5`, 175.5`}, {254.5`, 148.5`}, {43.5`, 174.5`}, {43.5`, 170.5`}, {196.5`, 174.5`}, {202.5`, 147.5`}, {297.5`, 174.5`}, {309.5`, 147.5`}, {63.5`, 148.5`}, {10.5`, 141.5`}, {143.5`, 117.5`}, {119.5`, 109.5`}, {67.5`, 94.5`}, {236.5`, 131.5`}, {293.5`, 127.5`}, {180.5`, 89.5`}, {312.5`, 146.5`}, {4.5`, 143.5`}, {18.5`, 97.5`}, {253.5`, 95.5`}, {301.5`, 98.5`}, {110.5`, 75.5`}, {313.5`, 93.5`}, {286.5`, 83.5`}, {52.5`, 80.5`}, {4.5`, 76.5`}, {236.5`, 82.5`}, {181.5`, 86.5`}, {187.5`, 80.5`}, {168.5`, 31.5`}, {297.5`, 37.5`}, {244.5`, 49.5`}, {59.5`, 29.5`}, {216.5`, 27.5`}, {125.5`, 38.5`}, {225.5`, 26.5`}, {280.5`, 23.5`}, {152.5`, 20.5`}, {110.5`, 3.5`}, {313.5`, 29.5`}, {199.5`, 7.5`}, {32.5`, 7.5`}, {85.5`, 3.5`}, {236.5`, 3.5`}, {4.5`, 25.5`}, {10.5`, 16.5`}, {281.5`, 4.5`}, {155.5`, 3.5`}, {4.5`, 3.5`}, {34.5`, 4.5`}, {199.5`, 4.5`}}, VertexSize -> 3 {1, 1}, VertexStyle -> Red, EdgeStyle -> Directive[Black]] which yields the first graph g. Then, the code
hm = ConvexHullMesh[ Transpose[ Select[{GraphEmbedding[g], VertexDegree[g]} // Transpose, #[[2]] == 1 &]][[1]]] gb = Graph[hm["Edges"], VertexCoordinates -> MeshCoordinates[hm], VertexSize -> 3 {1, 1}, VertexStyle -> Red, EdgeStyle -> Directive[Black]] yields
Now, how do I merge both graphs? I tried GraphUnion, but I would need the correct VertexCoordinates. Could it be simply an ordering problem? Any suggestion?