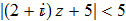3
$\begingroup$

I've done a little math and I got the following power series expansion of $\log z$ about $z_0=-2+i$.

$$\log z=\log(-2+i)+\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n(-2+i)^n}[z-(-2+i)]^n$$

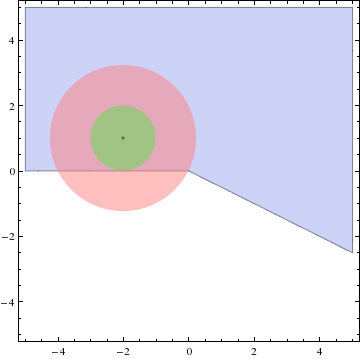
I've shown that the series converges on $|z-(-2+i)|<\sqrt5$ but I think it only agrees with $\log z$ on $|z-(-2+i)|<1$.

I have:

f = Function[z, Log[-2 + I] + Sum[(-1)^(n + 1)*(z - (-2 + I))^n/(n*(-2 + I)^n), {n, 1, Infinity}]]

The evaluation

f[-2 + I/2]

produces

log(-2 + I) + log(9/10 + I/5)

I'm wondering if there is an easy way to force this to a logarithm of a single number. I'm also wondering if someone has a suggestion on how to explore the convergence on the two regions defined above.

Improve this question
$\endgroup$

2 Answers 2

Reset to default
6
$\begingroup$

Maybe a graphical proof ?

Check your expansion by using SeriesCoefficient :

SeriesCoefficient[Log[z], {z, -2 + I, n}] // InputForm (* Piecewise[{{-((2/5 + I/5)^n/n), n >= 1}, {Log[-2 + I], n == 0}}, 0] *) Log[-2 + I] + Sum[-((2/5 + I/5)^n/n) (z - (-2 + I))^n, {n, 1, Infinity}] (* Log[-2 + I] + Log[(-(2/5) - I/5) z] *) diff = FullSimplify[ComplexExpand[f[x + I y] - Log[x + I y], TargetFunctions -> {Re, Im}], Assumptions :> {x ∈ Reals, y ∈ Reals}]; Show[RegionPlot[Abs[diff] < 10^-6, {x, -5, 5}, {y, -5, 5}], Graphics[{Black, PointSize[0.01], Point[{-2, 1}]}], Graphics[{Pink, Opacity[0.5], Disk[{-2, 1}, Sqrt[5]]}], Graphics[{Green, Opacity[0.3], Disk[{-2, 1}, 1]}]]

plot

Improve this answer
$\endgroup$
1
  • $\begingroup$ How about Plot3D[Abs[diff], {x, -5, 5}, {y, -5, 5}] or similar ? $\endgroup$ Commented Mar 31, 2013 at 17:41
4
$\begingroup$

It seems you are looking for a few things, the first is SumConvergence :

SumConvergence[(-1)^(n + 1)*(z - (-2 + I))^n/(n*(-2 + I)^n), n] // TraditionalForm

enter image description here

It is equivalent to your calculations since :

Abs @ Factor[5 + (2 + I) z] 
 Sqrt[5] Abs[(2 - I) + z]

Another thing you are lacking is FullSimplify in the definition of your function : 

FullSimplify[Log[-2 + I] + Log[9/10 + I/5]] 
Log[-2 + I/2]
Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.