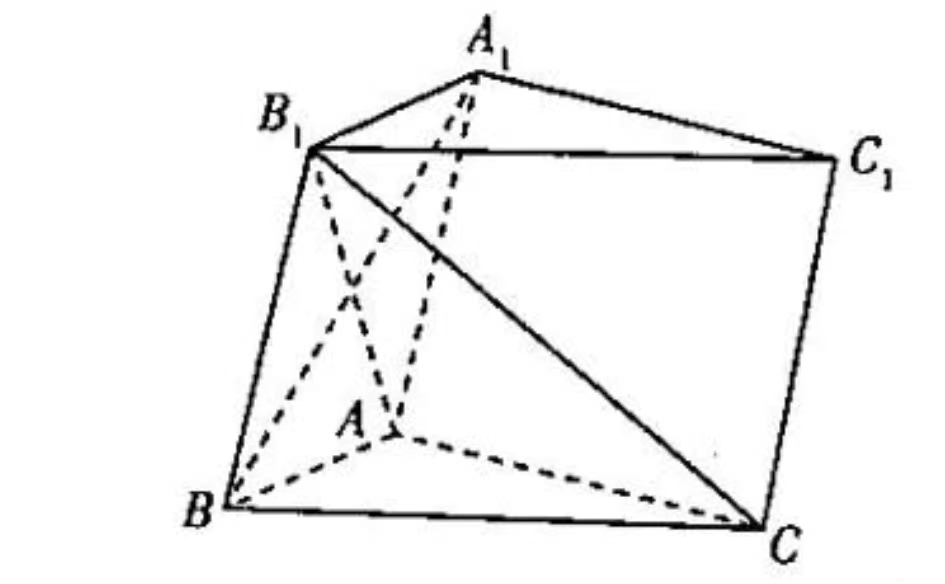
In the triangular prism ABC-A1B1C1, the quadrilateral AA1B1B is a diamond, AB is perpendicular to AC, plane AA1B1B is perpendicular to plane ABC, A1B is perpendicular to B1C, AB=AC=2, angle ABB1 equals 60 degrees, these are known conditions.
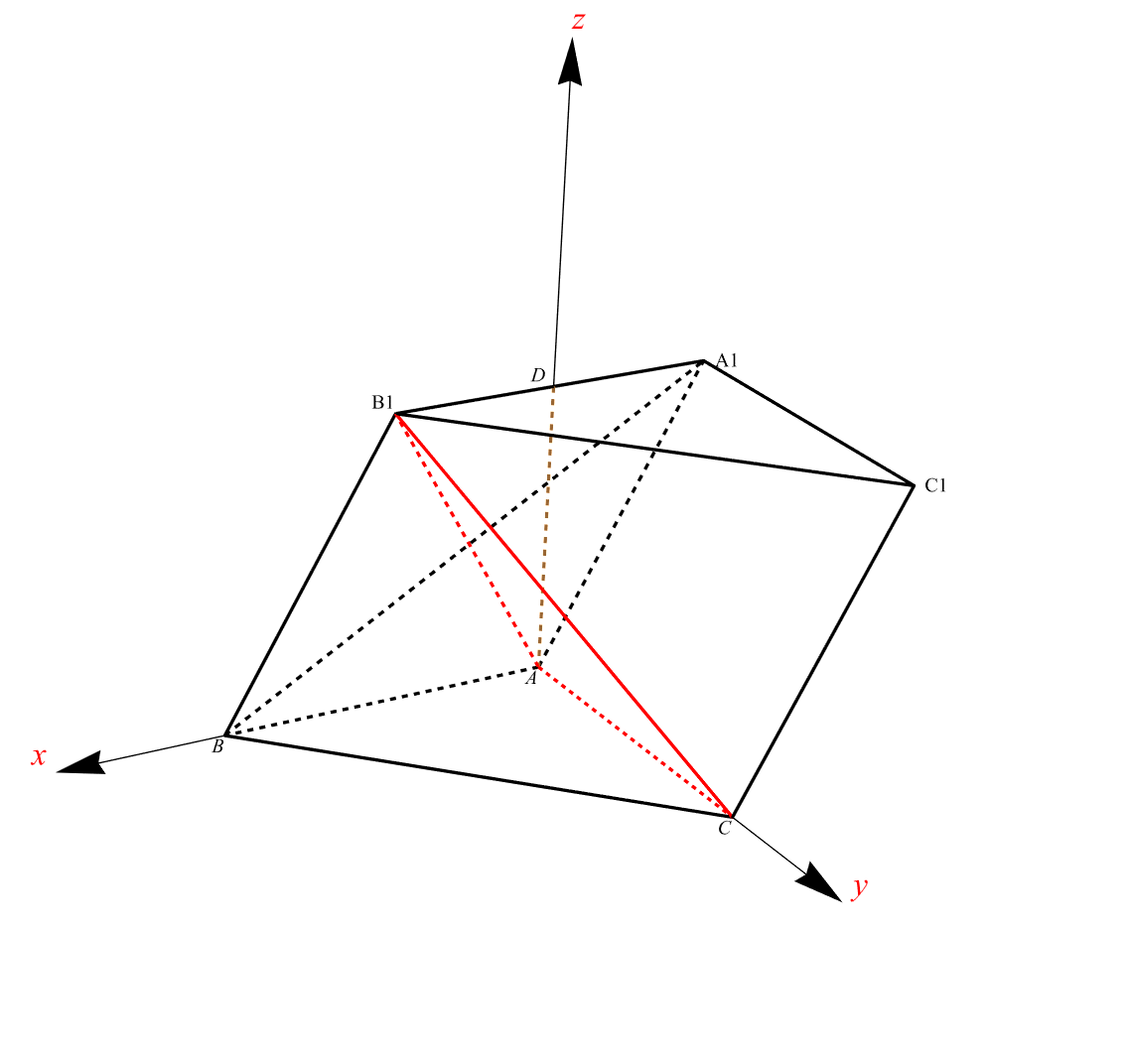
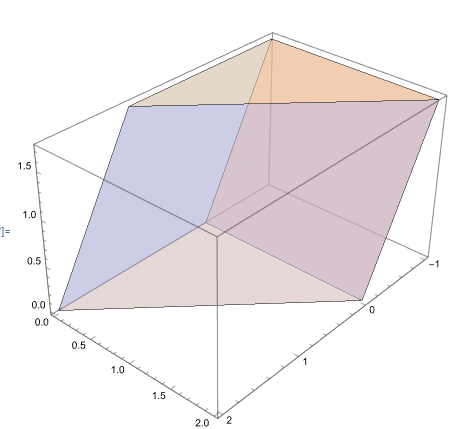
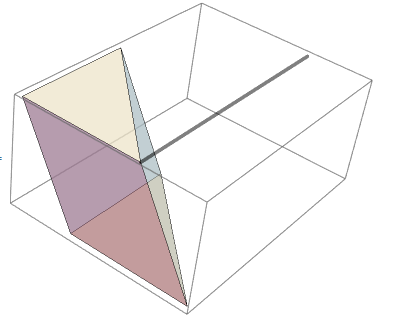
How can the software automatically draw the intersection line l between plane A1B1C1 and plane AB1C based on the spatial geometry?
Clear["Global`*"]; a = {0, 0, 0}; b = {2, 0, 0}; c = {0, 2, 0}; a1 = {-1, 0, Sqrt[3]}; b1 = {1, 0, Sqrt[3]}; c1 = {-1, 2, Sqrt[3]}; d = {0, 0, Sqrt[3]}; labels = {Text[Style[A, 12, FontFamily -> "Times"], a, {1, 1}], Text[Style[B, 12, FontFamily -> "Times"], b, {1, 1}], Text[Style[C, 12, FontFamily -> "Times"], c, {1, 1}], Text[Style[D, 12, FontFamily -> "Times"], d, {2, -1}], Text[Style[A1, 12, FontFamily -> "Times"], a1, {-2, 0}], Text[Style[B1, 12, FontFamily -> "Times"], b1, {1, -1}], Text[Style[C1, 12, FontFamily -> "Times"], c1, {-2, 0}]}; dashLines = {Dashed, AbsoluteThickness[2], {Brown, Line[{{d, a}}]}, {Red, Line[{{a, c}, {a, b1}}]}, {Black, Line[{{a, b}, {a, a1}}]}, {Black, Line[{{b, a1}}]}}; realLines = {AbsoluteThickness[2], Line[{{a1, b1}, {a1, c1}, {b1, c1}, {b, c}, {b, b1}, {c, c1}}], {Red, Line[{{c, b1}}]}}; Show[Graphics3D[{dashLines, realLines, labels}, Boxed -> False, ViewPoint -> {2, 3, 2}], Graphics3D[{Arrow[{{d, d + {0, 0, 2}}, {b, b + {1, 0, 0}}, {c, c + {0, 1, 0}}}], Text[Style["z", Red, 20, Italic, FontFamily -> "Times"], d + {0, 0, 2}, {-1, -1}], Text[Style["y", Red, 20, Italic, FontFamily -> "Times"], c + {0, 1, 0}, {-2, -1}], Text[Style["x", Red, 20, Italic, FontFamily -> "Times"], b + {1, 0, 0}, {2, -1}]}]] The spatial geometry has been drawn