0
$\begingroup$

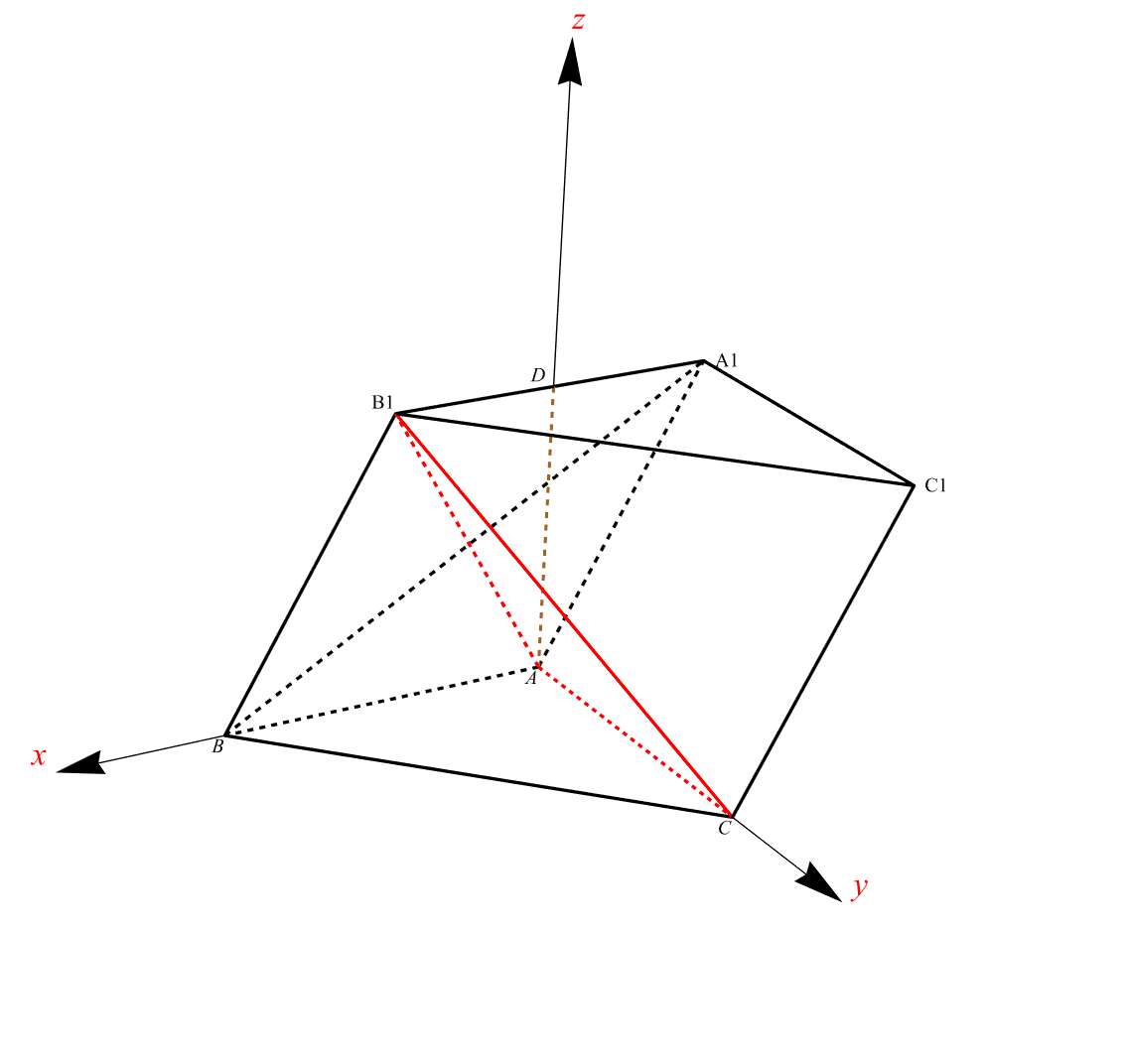
In the triangular prism ABC-A1B1C1, the quadrilateral AA1B1B is a diamond, AB is perpendicular to AC, plane AA1B1B is perpendicular to plane ABC, A1B is perpendicular to B1C, AB=AC=2, angle ABB1 equals 60 degrees, these are known conditions.

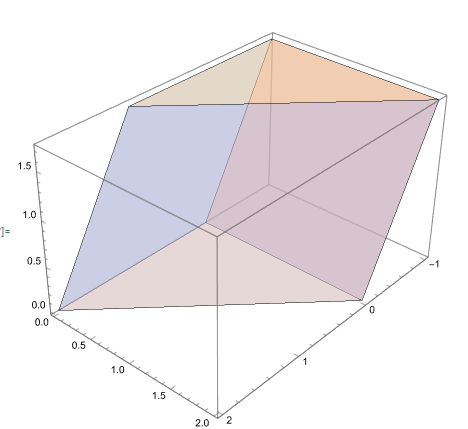
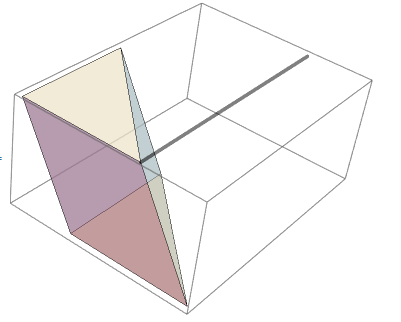
How can the software automatically draw the intersection line l between plane A1B1C1 and plane AB1C based on the spatial geometry?

enter image description here

Clear["Global`*"]; a = {0, 0, 0}; b = {2, 0, 0}; c = {0, 2, 0}; a1 = {-1, 0, Sqrt[3]}; b1 = {1, 0, Sqrt[3]}; c1 = {-1, 2, Sqrt[3]}; d = {0, 0, Sqrt[3]}; labels = {Text[Style[A, 12, FontFamily -> "Times"], a, {1, 1}], Text[Style[B, 12, FontFamily -> "Times"], b, {1, 1}], Text[Style[C, 12, FontFamily -> "Times"], c, {1, 1}], Text[Style[D, 12, FontFamily -> "Times"], d, {2, -1}], Text[Style[A1, 12, FontFamily -> "Times"], a1, {-2, 0}], Text[Style[B1, 12, FontFamily -> "Times"], b1, {1, -1}], Text[Style[C1, 12, FontFamily -> "Times"], c1, {-2, 0}]}; dashLines = {Dashed, AbsoluteThickness[2], {Brown, Line[{{d, a}}]}, {Red, Line[{{a, c}, {a, b1}}]}, {Black, Line[{{a, b}, {a, a1}}]}, {Black, Line[{{b, a1}}]}}; realLines = {AbsoluteThickness[2], Line[{{a1, b1}, {a1, c1}, {b1, c1}, {b, c}, {b, b1}, {c, c1}}], {Red, Line[{{c, b1}}]}}; Show[Graphics3D[{dashLines, realLines, labels}, Boxed -> False, ViewPoint -> {2, 3, 2}], Graphics3D[{Arrow[{{d, d + {0, 0, 2}}, {b, b + {1, 0, 0}}, {c, c + {0, 1, 0}}}], Text[Style["z", Red, 20, Italic, FontFamily -> "Times"], d + {0, 0, 2}, {-1, -1}], Text[Style["y", Red, 20, Italic, FontFamily -> "Times"], c + {0, 1, 0}, {-2, -1}], Text[Style["x", Red, 20, Italic, FontFamily -> "Times"], b + {1, 0, 0}, {2, -1}]}]]

The spatial geometry has been drawn

enter image description here

Improve this question
$\endgroup$

1 Answer 1

Reset to default
1
$\begingroup$

Let us first draw the Prism:

o = Cos[60 Degree]; si = Sin[60 Degree]; a = {0, 0, 0}; b = {2, 0, 0}; c = {0, 2, 0}; a1 = 2 {-co, 0, si}; b1 = {2 - 2 co, 0, 2 si}; c1 = 2 {-co, 1, si}; Graphics3D[{Opacity[0.5], Prism[{a, b, c, a1, b1, c1}]}, Boxed -> True, Axes -> True]

enter image description here

Now, the intersection line is contained in the plane a1b1c1 and also in the plane ab1c. Every point in a1b1c1 can be written by: {a1 + u1 (b1 - a1) + u2 (c1 - a1) with variables u1 and u2. Similar with plane ab1c: a + w1 (b1 - a) + w2 (c - a)with variables w1 and w2. We may therefore write the equation of the line and point p on the line:

eq = {a1 + u1 (b1 - a1) + u2 (c1 - a1) == a + w1 (b1 - a) + w2 (c - a)}; p[u2_] = a1 + u1 (b1 - a1) + u2 (c1 - a1) /. Solve[eq, {u1, u2, w1, w2}][[1]]

With this we may draw the line:

Graphics3D[{Opacity[0.5], Prism[{a, b, c, a1, b1, c1}], Thickness[0.01], Line[{b1, p[2]}]}]

enter image description here

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.