Introduction to Numerical Mathematics
This is the "Hello, World!" of PDEs (Partial Differential Equations). The Laplace or Diffusion Equation appears often in Physics, for example Heat Equation, Deforming, Fluid Dynamics, etc... As real life is 3D but we want to say "Hello, World!" and not sing "99 bottles of beer,..." this task is given in 1D. You may interpret this as a rubber robe tied to a wall on both ends with some force applied to it.
On a \$[0,1]\$ domain, find a function \$u\$ for given source function \$f\$ and boundary values \$u_L\$ and \$u_R\$ such that:
- \$-u'' = f\$
- \$u(0) = u_L\$
- \$u(1) = u_R\$
\$u''\$ denotes the second derivative of \$u\$
This can be solved purely theoretically but your task is it to solve it numerically on a discretized domain \$x\$ for \$N\$ points:
- \$x = \{\frac i {N-1} : 0 \le i \le N-1\}\$ or 1-based: \$\{\frac {i-1} {N-1} : 0 \le i \le N-1\}\$
- \$h = \frac 1 {N-1}\$ is the spacing
Input
- \$f\$ as a function, expression or string
- \$u_L\$, \$u_R\$ as floating point values
- \$N \ge 2\$ as an integer
Output
- Array, List, some sort of separated string of \$u\$ such that \$u_i = u(x_i)\$
Examples
Example 1
Input: \$f = -2\$, \$u_L = u_R = 0\$, \$N = 10\$ (Don't take \$f=-2\$ wrong, it is not a value but a constant function that returns \$-2\$ for all \$x\$. It is like a constant gravity force on our rope.)
Output: [-0.0, -0.09876543209876543, -0.1728395061728395, -0.22222222222222224, -0.24691358024691357, -0.24691358024691357, -0.22222222222222224, -0.1728395061728395, -0.09876543209876547, -0.0]
There exists an easy exact solution: \$u = -x(1-x)\$
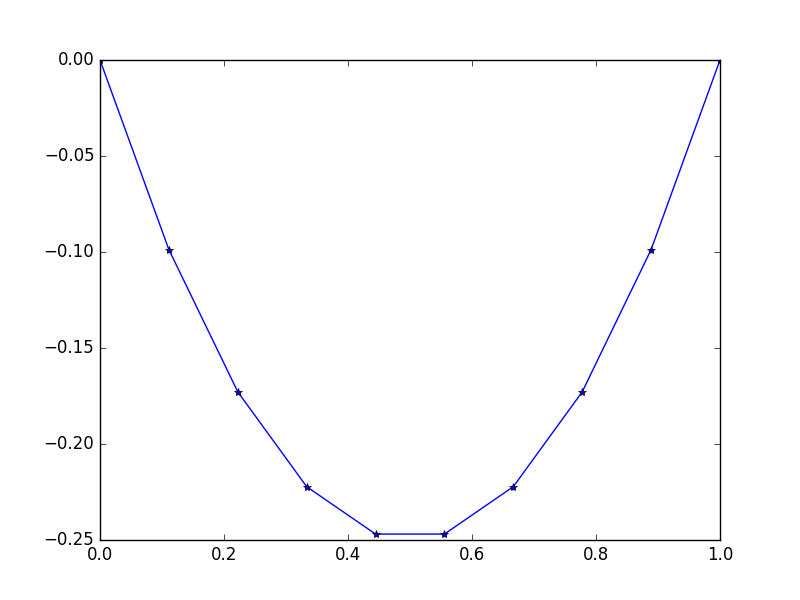
Example 2
Input: \$f = 10x\$, \$u_L = 0\$, \$u_R = 1\$, \$N = 15\$ (Here there is a lot of upwind on the right side)
Output: [ 0., 0.1898688, 0.37609329, 0.55502915, 0.72303207, 0.87645773, 1.01166181, 1.125, 1.21282799, 1.27150146, 1.29737609, 1.28680758, 1.2361516, 1.14176385, 1.]
The exact solution for this states: \$u = \frac 1 3(8x-5x^3)\$
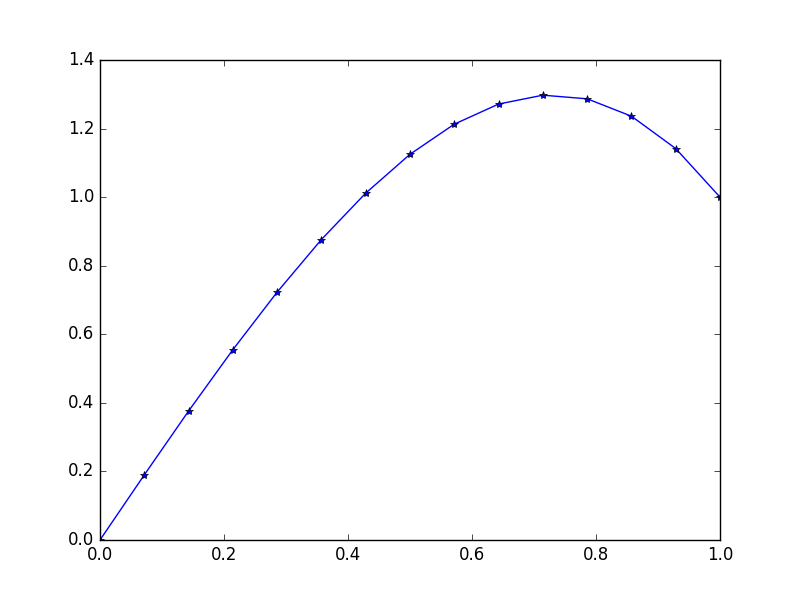
Example 3
Input: \$f = \sin(2\pi x)\$, \$u_L = u_R = 1\$, \$N = 20\$ (Someone broke gravity or there is a sort of up- and downwind)
Output: [ 1., 1.0083001, 1.01570075, 1.02139999, 1.0247802, 1.0254751, 1.02340937, 1.01880687, 1.01216636, 1.00420743, 0.99579257, 0.98783364, 0.98119313, 0.97659063, 0.9745249, 0.9752198, 0.97860001, 0.98429925, 0.9916999, 1.]
Here the exact solution is \$u = \frac {\sin(2πx)} {4π^2}+1\$
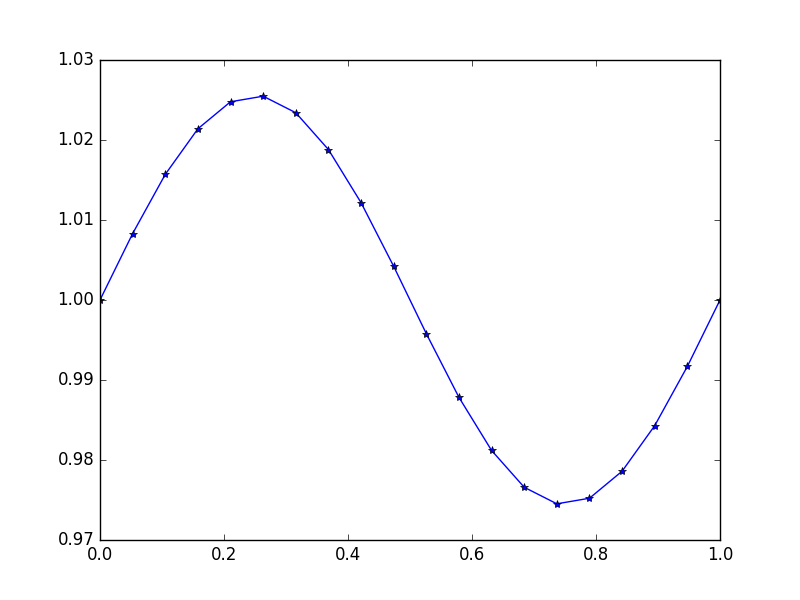
Example 4
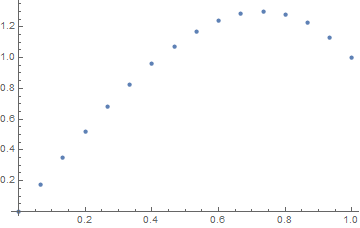
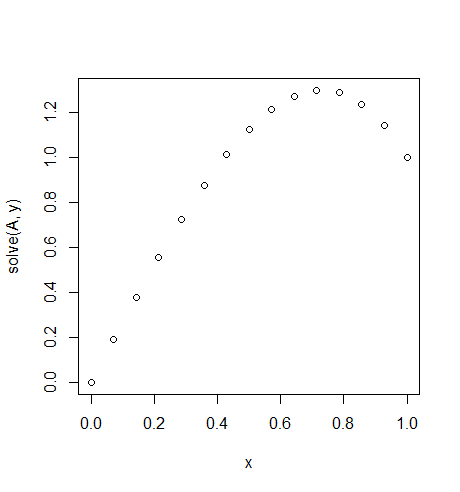
Input: \$f = \exp(x^2)\$, \$u_L = u_R = 0\$, \$N=30\$
Output: [ 0. 0.02021032 0.03923016 0.05705528 0.07367854 0.0890899 0.10327633 0.11622169 0.12790665 0.13830853 0.14740113 0.15515453 0.16153488 0.1665041 0.17001962 0.172034 0.17249459 0.17134303 0.16851482 0.1639387 0.15753606 0.1492202 0.13889553 0.12645668 0.11178744 0.09475961 0.07523169 0.05304738 0.02803389 0. ]
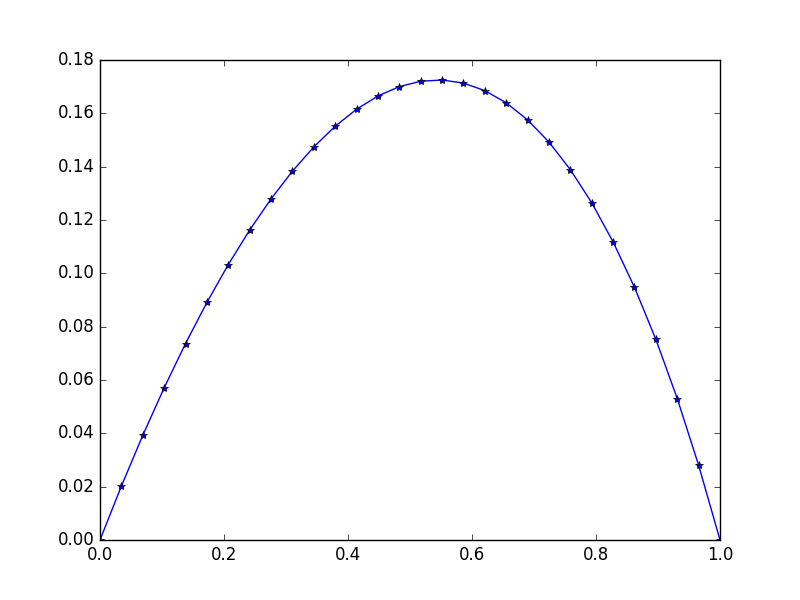
Note the slight asymmetry
FDM
One possible method to solve this is the Finite Difference Method:
- Rewrite \$-u_i'' = f_i\$ as \$\frac {-u_{i-1} + 2u_i - u_{i+1}} {h^2} = f_i\$, which equals \$-u_{i-1} + 2u_i - u_{i+1} = h^2 f_i\$
- Setup the equations:
$$ u_0 = u_L \\ \frac {-u_0 + 2u_1 - u_2} {h^2} = f_1 \\ \frac {-u_1 + 2u_2 - u_3} {h^2} = f_2 \\ \dots = \dots \\ \frac {-u_{n-3} + 2u_{n-2} - u_{n-1}} {h^2} = f_{n-2} \\ u_{n-1} = u_R $$
- Which are equal to a matrix-vector equation:
$$ \begin{pmatrix} 1 & & & & & & \\ -1 & 2 & -1 & & & & \\ & -1 & 2& -1& & & \\ & & \ddots & \ddots & \ddots & & \\ & & & -1 & 2 & -1 & \\ & & & & -1 & 2 & -1 \\ & & & & & & 1 \end{pmatrix} \begin{pmatrix} u_0 \\ u_1 \\ u_2 \\ \vdots \\ u_{n-3} \\ u_{n-2} \\ u_{n-1} \end{pmatrix} = \begin{pmatrix} u_L \\ h^2 f_1 \\ h^2 f_2 \\ \vdots \\ h^2 f_{n-3} \\ h^2 f_{n-2} \\ u_R \end{pmatrix} $$
- Solve this equation and output the \$u_i\$
One implementation of this for demonstration in Python:
import matplotlib.pyplot as plt import numpy as np def laplace(f, uL, uR, N): h = 1./(N-1) x = [i*h for i in range(N)] A = np.zeros((N,N)) b = np.zeros((N,)) A[0,0] = 1 b[0] = uL for i in range(1,N-1): A[i,i-1] = -1 A[i,i] = 2 A[i,i+1] = -1 b[i] = h**2*f(x[i]) A[N-1,N-1] = 1 b[N-1] = uR u = np.linalg.solve(A,b) plt.plot(x,u,'*-') plt.show() return u print laplace(lambda x:-2, 0, 0, 10) print laplace(lambda x:10*x, 0, 1, 15) print laplace(lambda x:np.sin(2*np.pi*x), 1, 1, 20) Alternative implementation without Matrix Algebra (using the Jacobi method)
def laplace(f, uL, uR, N): h=1./(N-1) b=[f(i*h)*h*h for i in range(N)] b[0],b[-1]=uL,uR u = [0]*N def residual(): return np.sqrt(sum(r*r for r in[b[i] + u[i-1] - 2*u[i] + u[i+1] for i in range(1,N-1)])) def jacobi(): return [uL] + [0.5*(b[i] + u[i-1] + u[i+1]) for i in range(1,N-1)] + [uR] while residual() > 1e-6: u = jacobi() return u You may however use any other method to solve the Laplace equation. If you use an iterative method, you should iterate until the residual \$|b-Au| < 10^{-6}\$, with \$b\$ being the right hand side vector \$u_L,f_1 h^2,f_2 h^2, \dots\$
Notes
Depending on your solution method you may not solve the examples exactly to the given solutions. At least for \$N \to \infty\$ the error should approach zero.
Standard loopholes are disallowed, built-ins for PDEs are allowed.
Bonus
A bonus of -30% for displaying the solution, either graphical or ASCII-art.
Winning
This is codegolf, so shortest code in bytes wins!

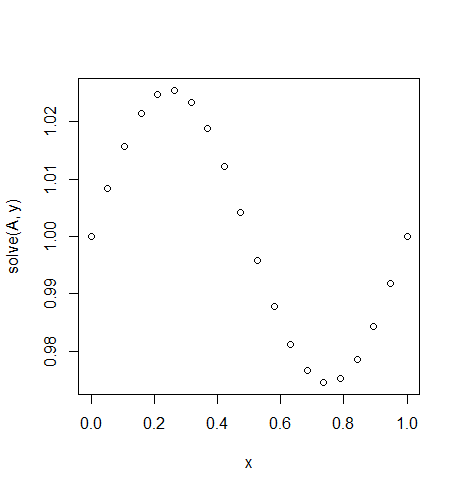
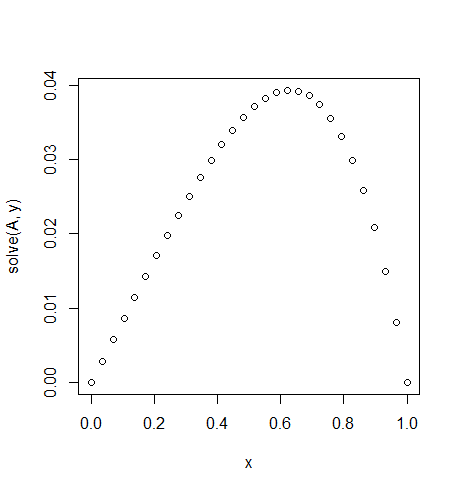
f(x) = exp(x^2). \$\endgroup\$log(log(x))orsqrt(1-x^4)which do have an integral, which is however not expressible in elementary functions. \$\endgroup\$u(x) = 1/2 (-sqrt(π) x erfi(x)+sqrt(π) erfi(1) x+e^(x^2)-e x+x-1)is not exactly calculable. \$\endgroup\$