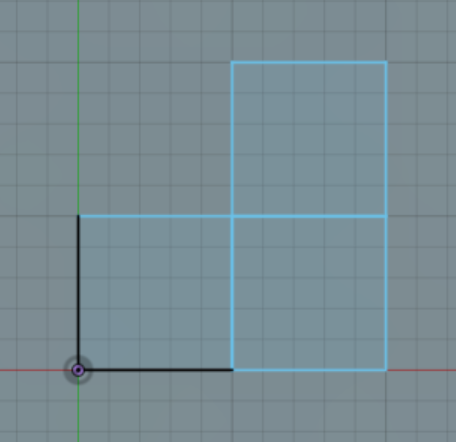
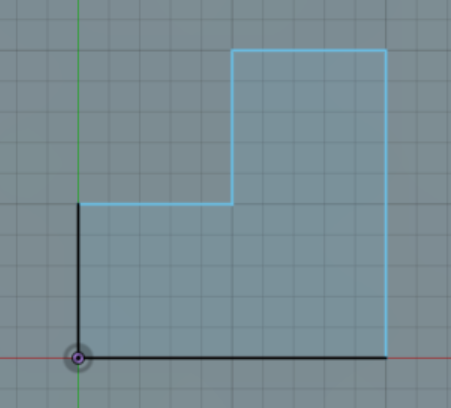
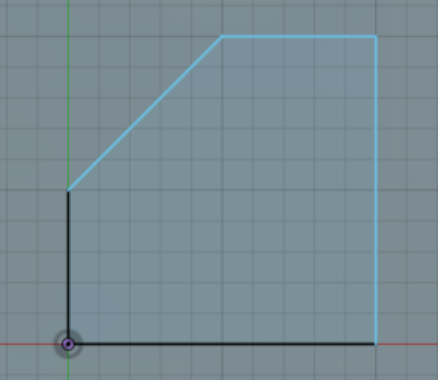
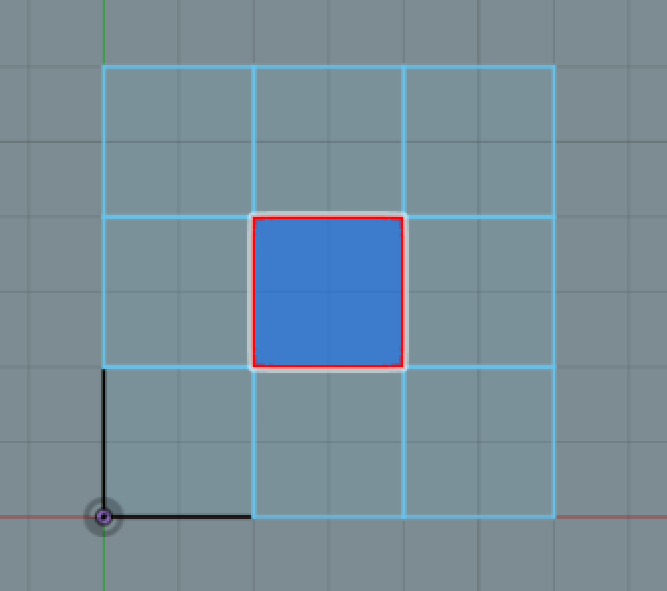
Is there an algorithm where I provide a list of non-overlapping squares, for example:
sq1 = [(0, 0), (0, 1), (1, 1), (1, 0), (0, 0)] sq2 = [(1, 0), (1, 1), (2, 1), (2, 0), (1, 0)] sq3 = [(1, 1), (1, 2), (2, 2), (2, 1), (1, 1)] and it will return some sort of "collinear convex hull" where the results will be?:
res = [(0,0), (0,1), (1,1), (1,2), (2,2), (2,0), (0,0)] If I try the regular convex hull algorighm, it returns
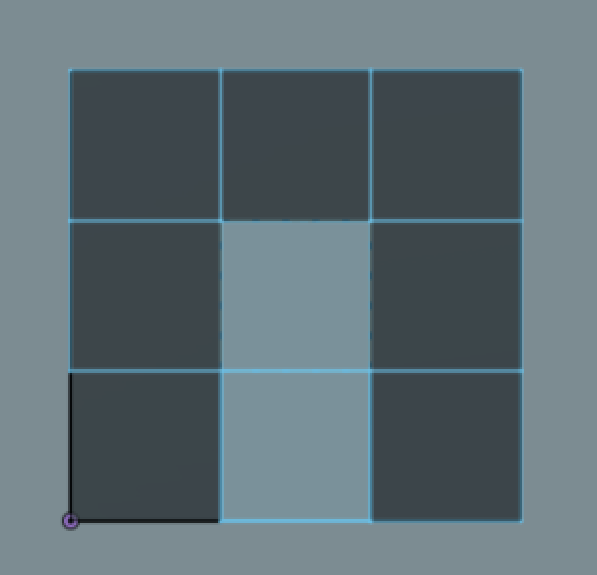
Update: Every square will share at least one side with another, but if for examples there is an empty square in the middle of a 9x9 grid:
sq1 = [(0, 0), (0, 1), (1, 1), (1, 0), (0, 0)] sq2 = [(0, 1), (0, 2), (1, 2), (1, 1), (0, 1)] sq3 = [(0, 2), (0, 3), (1, 3), (1, 2), (0, 2)] sq4 = [(1, 2), (1, 3), (2, 3), (2, 2), (1, 2)] sq5 = [(2, 2), (2, 3), (3, 3), (3, 2), (2, 2)] sq6 = [(2, 1), (2, 2), (3, 2), (3, 1), (2, 1)] sq7 = [(2, 0), (2, 1), (3, 1), (3, 0), (2, 0)] sq8 = [(1, 0), (1, 1), (2, 1), (2, 0), (1, 0)] ret = [(0, 0), (0, 3), (3, 3), (3, 0), (0, 0)] So ignoring the "hole" in the middle. This would be the same results generated by the "regular" Convex Hull algorithm.
However, if instead I have:
sq1 = [(0, 0), (0, 1), (1, 1), (1, 0), (0, 0)] sq2 = [(0, 1), (0, 2), (1, 2), (1, 1), (0, 1)] sq3 = [(0, 2), (0, 3), (1, 3), (1, 2), (0, 2)] sq4 = [(1, 2), (1, 3), (2, 3), (2, 2), (1, 2)] sq5 = [(2, 2), (2, 3), (3, 3), (3, 2), (2, 2)] sq6 = [(2, 1), (2, 2), (3, 2), (3, 1), (2, 1)] sq7 = [(2, 0), (2, 1), (3, 1), (3, 0), (2, 0)] Then the result should be:
ret = [(0, 0), (0, 3), (3, 3), (3, 0), (2, 0), (2, 2), (1, 2), (1, 0), (0, 0)]