What Is the Best First Order IIR (AR Filter) Approximation to a Moving Average Filter (FIR Filter)?

OK, let's try to derive the best: $$ \begin{array}{lcl} y[n] &=& \alpha x[n] + (1 - \alpha) y[n - 1] \\ &=& \alpha x[n] + (1 - \alpha) \alpha x[n-1] + (1 - \alpha)^2 y[n - 2]\\ &=& \alpha x[n] + (1 - \alpha) \alpha x[n-1] + (1 - \alpha)^2 \alpha x[n-2] + (1 - \alpha)^3 y[n - 3]\\ \end{array} $$ so that the coefficient of $x[n-m]$ is $\alpha(1-\alpha)^m$.

The best mean-square approximation will minimize: $$ \begin{array}{lcl} J(\alpha) &=& \sum_{m=0}^{k-1} (\alpha(1-\alpha)^m - \frac{1}{k})^2 + \sum_{m=k}^\infty \alpha^2(1-\alpha)^{2m}\\ &=& \sum_{m=0}^{k-1} \left(\alpha^2(1-\alpha)^{2m} - \frac{2}{k}\alpha(1-\alpha)^m + \frac{1}{k^2}\right) + \alpha^2 (1-\alpha)^{2k} \sum_{m=0}^\infty (1-\alpha)^{2m} \\ &=& \alpha^2\frac{1- (1-\alpha)^{2k}}{1 - (1-\alpha)^2} + \frac{2\alpha}{k} \frac{1 - (1 - \alpha)^k}{1 - (1 - \alpha)} + \frac{\alpha^2(1-\alpha)^{2k}}{1 - (1 - \alpha)^2}+ \frac{1}{k}\\ &=& \frac{\alpha^2}{1 - (1 - \alpha)^2} + \frac{2}{k} (1-(1-\alpha)^k) + \frac{1}{k}\\ &=& \frac{\alpha^2}{2\alpha - \alpha^2 }+ \frac{2}{k} (1-(1-\alpha)^k)+ \frac{1}{k}\\ &=& \frac{\alpha}{2 - \alpha }+ \frac{2}{k} (1-(1-\alpha)^k)+ \frac{1}{k}\\ \end{array} $$ because the FIR coefficients are zero for $m > k - 1$.

Next step is to take derivatives and equate to zero.

Looking at a plot of the derived $J$ for $K = 1000$ and $\alpha$ from 0 to 1, it looks like the problem (as I've set it up) is ill-posed, because the best answer is $\alpha = 0$.

I think there's a mistake here. The way it should be according to my calculations is:

$$ \begin{array}{lcl} J(\alpha) &=& \sum_{m=0}^{k-1} (\alpha(1-\alpha)^m - \frac{1}{k})^2 + \sum_{m=k}^\infty \alpha^2(1-\alpha)^{2m} \\ &=& \sum_{m=0}^{k-1} \left(\alpha^2(1-\alpha)^{2m} - \frac{2}{k}\alpha(1-\alpha)^m + \frac{1}{k^2}\right) + \alpha^2 (1-\alpha)^{2k} \sum_{m=0}^\infty (1-\alpha)^{2m} \\ &=& \alpha^2\frac{1- (1-\alpha)^{2k}}{1 - (1-\alpha)^2} - \frac{2\alpha}{k} \frac{1 - (1 - \alpha)^k}{1 - (1 - \alpha)} + \frac{1}{k} + \frac{\alpha^2(1-\alpha)^{2k}}{1 - (1 - \alpha)^2} \end{array} $$

Simplifying it according to Mathematica yields:

$$ J(\alpha) = \frac{\alpha}{2 - \alpha} + \frac{2 {(1 - \alpha)}^{k} -1}{k} $$

Using the following code on MATLAB yields something equivalent though different:

syms a k; expr1 = (a ^ 2) * ((1 - ((1 - a) ^ (2 * k))) / (1 - ((1 - a) ^ 2))); expr2 = ((2 * a) / k) * ((1 - ((1 - a) ^ (k))) / (1 - (1 - a))); expr3 = (1 / k); expr4 = ((a ^ 2) * ((1 - a) ^ (2 * k))) / (1 - ((1 - a) ^ (2))); simpExpr = simplify(expr1 - expr2 + expr3 + expr4); 

$$ J(\alpha) = \frac{-2}{\alpha - 2} - \frac{k - 2{(1 - \alpha)}^{k} + 1}{k} $$

Anyhow, those functions do have minimum.

So let's assume that we really only care about the approximation over the support (length) of the FIR filter. In that case, the optimization problem is just: $$ J_2(\alpha) = \sum_{m=0}^{k-1} (\alpha(1-\alpha)^m - \frac{1}{k})^2 $$

Plotting $J_2(\alpha)$ for various values of $K$ versus $\alpha$ results in the date in the plots and table below.

For $K$ = 8. $\alpha_{\tt min}$ = 0.1533333
For $K$ = 16. $\alpha_{\tt min}$ = 0.08
For $K$ = 24. $\alpha_{\tt min}$ = 0.0533333
For $K$ = 32. $\alpha_{\tt min}$ = 0.04
For $K$ = 40. $\alpha_{\tt min}$ = 0.0333333
For $K$ = 48. $\alpha_{\tt min}$ = 0.0266667
For $K$ = 56. $\alpha_{\tt min}$ = 0.0233333
For $K$ = 64. $\alpha_{\tt min}$ = 0.02
For $K$ = 72. $\alpha_{\tt min}$ = 0.0166667

The red dashed lines are $1/K$ and the green lines are $\alpha_{\tt min}$, the value of $\alpha$ that minimizes $J_2(\alpha)$ (chosen from $\tt alpha = [0:.01:1]/3;$).

There's a nice discussion of this problem in Embedded Signal Processing with the Micro Signal Architecture, roughly between pages 63 and 69. On page 63, it includes a derivation of the exact recursive moving average filter (which niaren gave in his answer),

$$ H(z) = { 1 \over{N} } { 1 - z^{-N} \over { 1 - z^{-1} } }. $$

For convenience with respect to the following discussion, it corresponds to the following difference equation:

$$ y_n = y_{n-1} + {1\over{N} }(x_n - x_{n-N}). $$

The approximation which puts the filter into the form you specified requires assuming that $x_{n-N} \approx y_{n-1}$, because (and I quote from pg. 68) "$y_{n-1}$ is the average of $x_n$ samples". That approximation allows us to simplify the preceding difference equation as follows:

$$ \begin{array}\\ y_{n} = y_{n-1} + {1\over{N}}(x_n - y_{n-1}) \\ y_{n} = y_{n-1} - {1\over{N}} y_{n-1} + {1\over{N}}x_n \\ y_{n} = (1-{1\over{N}})y_{n-1} + {1\over{N}}x_n. \end{array} $$

Setting $\alpha = {1\over{N}}$, we arrive at your original form, $y_{n} = \alpha x_n + (1-\alpha)y_{n-1}$, which shows that the coefficient you want (with respect to this approximation) is exactly $1\over{N}$ (where $N$ is the number of samples).

Is this approximation the "best" in some respect? It's certainly elegant. Here's how the magnitude response compares [at 44.1kHz] for N = 3, and as N increases to 10 (approximation in blue):

As Peter's answer suggests, approximating an FIR filter with a recursive filter can be problematic under a least squares norm. An extensive discussion of how to solve this problem in general can be found in JOS's thesis, Techniques for Digital Filter Design and System Identification with Application to the Violin. He advocates the use of the Hankel Norm, but in cases where the phase response doesn't matter, he also covers Kopec's Method, which might work well in this case (and uses an $L^2$ norm). A broad overview of the techniques in the thesis can be found here. They may yield other interesting approximations.

Based in experimental tests with k in range (2 to 100) the best fit (sum squared error) gives a relation of alfa = 1/k^0.865 being k number of samples for MovAvg filter

I stumbled upon this old question and I would like to share my solution. As mentioned in other answers, there is no analytical solution, but the function to be minimized behaves nicely and the optimal value of $\alpha$ can be found easily with a few Newton iterations. There is also a formula to check the optimality of the result.

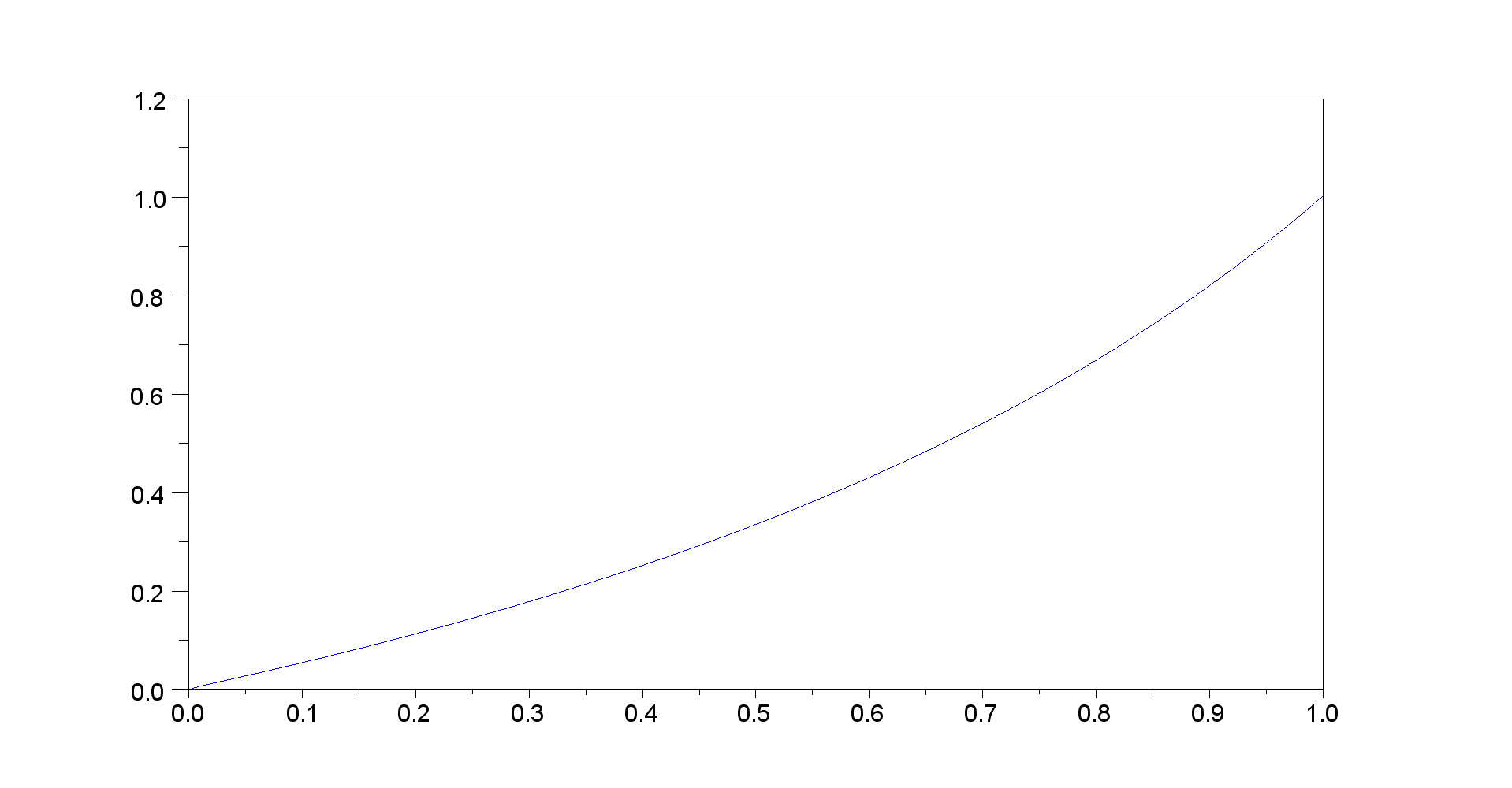
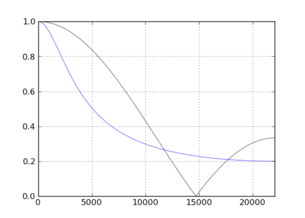
The impulse response of the length $N$ FIR moving average filter is given by

$$h_{FIR}[n]=\frac{1}{N}(u[n]-u[n-N])\tag{1}$$

where $u[n]$ is the unit step function. The first order IIR filter

$$y[n]=\alpha x[n]+(1-\alpha)y[n-1]\tag{2}$$

has the impulse response

$$h_{IIR}[n]=\alpha(1-\alpha)^nu[n]\tag{3}$$

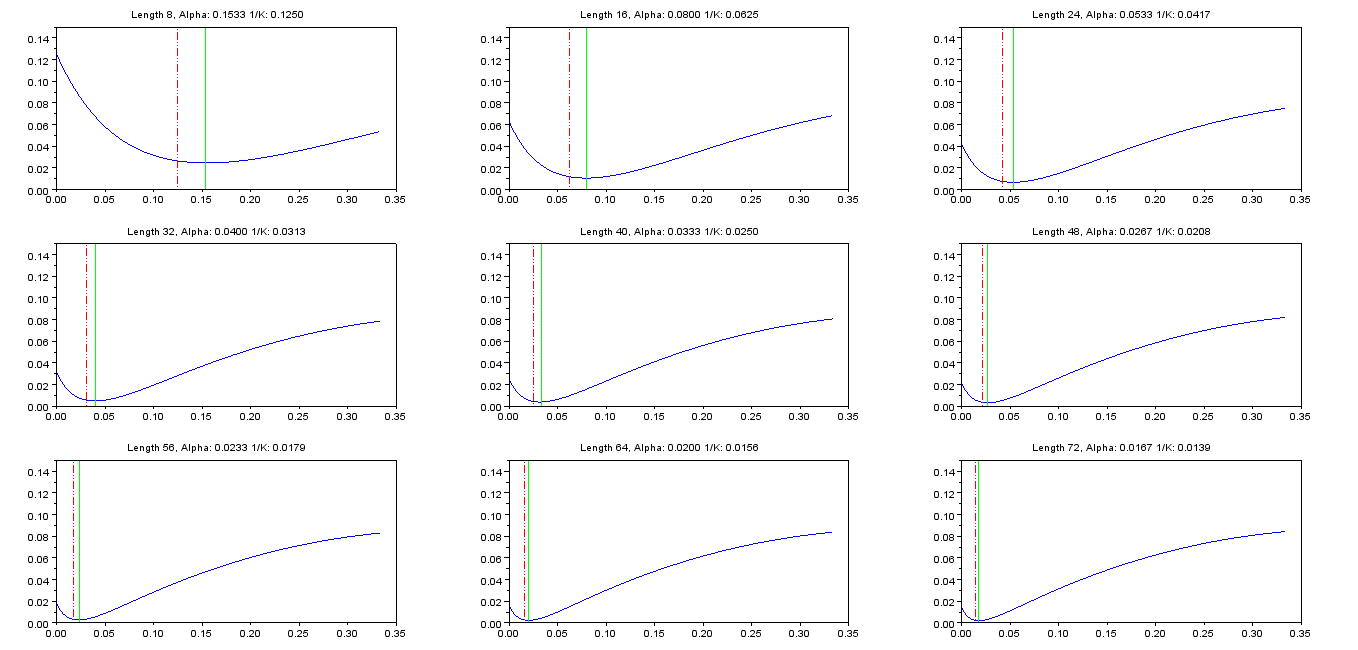
The goal is now to minimize the squared error

$$\epsilon=\sum_{n=0}^{\infty}\left(h_{FIR}[n]-h_{IIR}[n]\right)^2\tag{4}$$

Using $(1)$ and $(3)$, the error can be written as

$$\begin{align}\epsilon(\alpha)&=\sum_{n=0}^{N-1}\left(\alpha(1-\alpha)^n-\frac{1}{N}\right)^2+\sum_{n=N}^{\infty}\alpha^2(1-\alpha)^{2n}\\&=\alpha^2\sum_{n=0}^{\infty}(1-\alpha)^{2n}-\frac{2\alpha}{N}\sum_{n=0}^{N-1}(1-\alpha)^n+\sum_{n=0}^{N-1}\frac{1}{N^2}\\&=\frac{\alpha^2}{1-(1-\alpha)^2}-\frac{2\alpha}{N}\frac{1-(1-\alpha)^N}{1-(1-\alpha)}+\frac{1}{N}\\&=\frac{\alpha}{2-\alpha}-\frac{2}{N}\left(1-(1-\alpha)^N\right)+\frac{1}{N},\qquad 0<\alpha<2\tag{5}\end{align}$$

This expression is very similar to the one given in this answer, but it's not identical. The restriction on $\alpha$ in $(5)$ makes sure that the infinite sum converges, and it is identical to the stability condition for the IIR filter given by $(2)$.

Setting the derivative of $(5)$ to zero results in

$$(1-\alpha)^{N-1}(2-\alpha)^2=1\tag{6}$$

Note that the optimal $\alpha$ must be in the interval $(0,1]$ because larger values of $\alpha$ result in an alternating impulse response $(3)$, which cannot approximate the constant impulse repsonse of the FIR moving average filter.

Taking the square root of $(6)$ and introducing $\beta=1-\alpha$, we obtain

$$\beta^{(N+1)/2}+\beta^{(N-1)/2}-1=0\tag{7}$$

This equation cannot be solved analytically for $\beta$, but it can be solved for $N$:

$$N=-2\frac{\log(1+\beta)}{\log(\beta)},\qquad \beta\neq 0\tag{8}$$

Equation $(8)$ can be used to double-check a numerical solution of $(7)$; it must return the specified value of $N$.

Equation $(7)$ can be solved with a few lines of (Matlab/Octave) code:

 N = 50; % desired filter length of FIR moving average filter if ( N == 1 ) % no iteration for trivial case b = 0; else % Newton iteration b = 1; % starting value Nit = 7; n = (N+1)/2; for k = 1:Nit, f = b^n + b^(n-1) -1; fp = n*b^(n-1) + (n-1)*b^(n-2); b = b - f/fp; end % check result N0 = -2*log(1+b)/log(b) + 1 % must equal N end a = 1 - b; 

Below is a table with the optimal values of $\alpha$ for a range of filter lengths $N$:

 N alpha 1 1.0000e+00 2 5.3443e-01 3 3.8197e-01 4 2.9839e-01 5 2.4512e-01 6 2.0809e-01 7 1.8083e-01 8 1.5990e-01 9 1.4333e-01 10 1.2987e-01 20 6.7023e-02 30 4.5175e-02 40 3.4071e-02 50 2.7349e-02 60 2.2842e-02 70 1.9611e-02 80 1.7180e-02 90 1.5286e-02 100 1.3768e-02 200 6.9076e-03 300 4.6103e-03 400 3.4597e-03 500 2.7688e-03 600 2.3078e-03 700 1.9785e-03 800 1.7314e-03 900 1.5391e-03 1000 1.3853e-03