4
$\begingroup$

I have for example the following grid:

range = Range[0, 4, 0.5]; Graphics[Frame -> True, GridLines -> {range, range}, PlotRange -> {{0, 4}, {0, 4}}, Ticks -> {Automatic}, ImageSize -> Medium]

enter image description here

How can I plot a grid where the distance between axes numbers is 1 cm?

Improve this question
$\endgroup$
3
  • $\begingroup$ Centimeters are relative, not all screens have the same dpi. $\endgroup$ Commented Dec 12, 2016 at 11:30
  • $\begingroup$ If this is not possible at the screen, how can it be done in the printout. $\endgroup$ Commented Dec 12, 2016 at 11:34
  • 1
    $\begingroup$ Possible duplicates: (5442), (77129) $\endgroup$ Commented Dec 12, 2016 at 12:34

1 Answer 1

Reset to default
10
$\begingroup$

You need to:

  • Control the relationship between plot coordinates and the image size. This means that all settings that affect this must be set manually, and must not be left to chance

  • Set the correct image size.

In Mathematica, there are plot coordinates, scaled coordinates and absolute coordinates. Please read here:

For this task we need to work with plot coordinates and absolute ones. Absolute coordinates are given in printer's points.

Define the centimetre:

cm = 72/2.54 (* 72 points in an inch, 2.54 cm in an inch *)

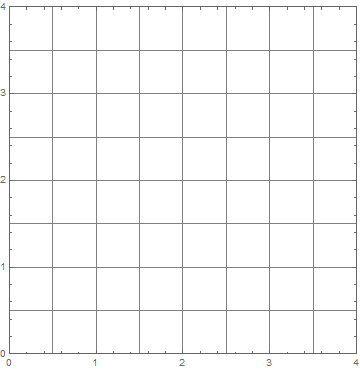
First step: eliminate all sorts of margins and paddings, to make sure that the frame is precisely on the edge of the image:

range = Range[0, 4, 0.5]; g = Graphics[Frame -> True, GridLines -> {range, range}, PlotRange -> {{0, 4}, {0, 4}}, Ticks -> {Automatic}, ImageSize -> 8 cm, PlotRangePadding -> None, ImagePadding -> None, ImageMargins -> 0]

enter image description here

It's clear that now the image size should be 8 cm, so we set it to that. But the labels are cut off.

Next step: manually set the ImagePadding to leave enough room for ticks labels. This is specified in printer's points. We need to increase the image size accrodingly. I am lazy so I'll set the same padding on all sides.

range = Range[0, 4, 0.5]; g = Graphics[Frame -> True, GridLines -> {range, range}, PlotRange -> {{0, 4}, {0, 4}}, Ticks -> {Automatic}, ImageSize -> 8 cm + 2*15 (* allow for 15 pt ImagePadding on both sides *), PlotRangePadding -> None, ImagePadding -> 15, ImageMargins -> 0]

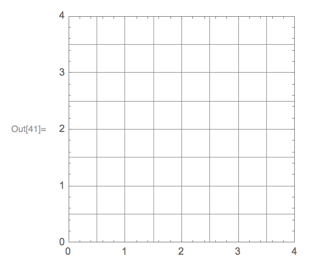
enter image description here

Now export to PDF,

Export["grid.pdf", g]

and print the result. In the print settings make sure to set the scale to 100%. Often the default is automatic, which tends to scale the document to fill the page.

Hint: Do use Export. Do not use right click, Save As... Read here: Graphics elements do not line up perfectly in exported PDFs

If you need to display at a given size on a screen, you must do some measurements and discover the true pixel density ("dpi") of your screen. Then scale the graphics accordingly using e.g. Magnify[g, factor].

Improve this answer
$\endgroup$
4
  • $\begingroup$ Great explanation ... thank you $\endgroup$ Commented Dec 12, 2016 at 11:42
  • 1
    $\begingroup$ @MichaelE2 Of course, thank you! $\endgroup$ Commented Dec 12, 2016 at 11:56
  • 3
    $\begingroup$ To be accurate, Mathematica, like nearly all software, uses Postscript point. TeX, which predates most desktop publishing software, uses printer's points, which are 0.9963 times smaller. I had to correct for this in MaTeX to match the two up. $\endgroup$ Commented Dec 12, 2016 at 12:01
  • 1
    $\begingroup$ You may also use the builtin unit functions. Define cmToDpp = QuantityMagnitude@UnitConvert[Quantity[#, "Centimeters"], "DesktopPublishingPoints"] &. Then cmToDpp@8 and so on. (+1) $\endgroup$ Commented Dec 12, 2016 at 21:49

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.