2
$\begingroup$

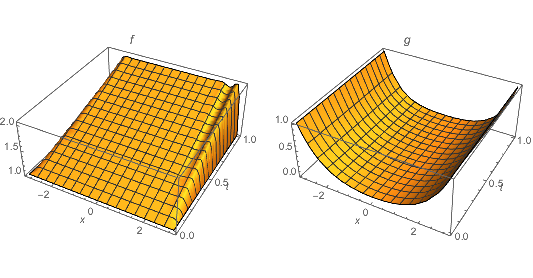
Say I want to solve the following set of PDE's (my actual equations are way more complicated, this is just a simplified example to show the structure): $$\begin{align} \partial_t f(x,t)&=1-g(x,t)\partial_x f(x,t)\\ \partial_{xx} g(x,t)&=g(x,t)f(x,t) \end{align} $$

with boundary + initial conditions $$ \begin{align} f(x,t=0)&=1& f(-\pi,t)&=f(\pi,t)=1 & g(-\pi,t)&=g(\pi,t)=1 \end{align} $$

Note that $g$ does not have an equation which contain a time derivative, but rather at each time step it is assumed to satisfy a spatial ODE. For example, at $t=0$ it satisfies the equation $$g''(x)=g(x)\qquad g(\pi)=g(-\pi)=1$$ whose solution is $$g(x,t=0)=\frac{\cosh(x)}{\cosh(\pi)}\ .$$ Note that this initial condition for $g(x,t=0)$ was not specified in the problem definition as it can be inferred from the other conditions.

If I just feed these equations to Mathematica (version 10.4.1 for Linux), I get an error message:

NDSolve[{ D[f[x, t], t] == 1 - D[f[x, t], x] g[x, t], D[g[x, t], x, x] == g[x, t] f[x, t], f[x, 0] == 1, f[-π, t] == f[π, t] == 1, g[-π, t] == g[π, t] == 1 }, {f, g}, {x, -π, π}, {t, 0, 1}]

enter image description here

So I thought of a workaround - to define a function that accepts $f(x,t)$ as an input and spits out the solution to the spatial ODE that $g$ satisfies:

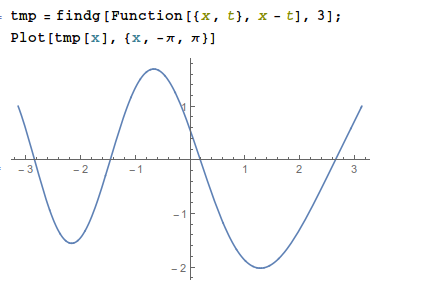
findg[f_, t_] := gt /. First@NDSolve[{ gt''[x] == gt[x] f[x, t], gt[-π] == gt[π] == 1 }, gt, {x, -π, π}]

This function works great, as you can see here:

enter image description here

However, I can't find a way to feed this into NDSolve. Running this

NDSolve[{ D[f[x, t], t] == 1 - D[f[x, t], x] findg[f[x, t], t], f[x, 0] == 1, f[-π, t] == f[π, t] == 1, }, f, {x, -π, π}, {t, 0, 1}]

gives an error message:

enter image description here

I think what happens is that the outer NDSolve does not pass a function to findg but rather the evaluated function at x,t. Any hints on how to solve this (or NDSolve this :)) would be much appreciated.

Improve this question
$\endgroup$
2
  • 1
    $\begingroup$ The f[x, t] that is passed to findg by NDSolve is a number, not a function, so the f[x, t] inside findg is something like 1.[x, t], which leads to the error message. And f by itself is a symbol, not a function, so calling findg[f, t] won't work either. (Not sure how to work around it...) $\endgroup$ Commented May 19, 2016 at 11:28
  • $\begingroup$ @MichaelE2 That is what I suspected. Can you not do some trick with Hold and Release and the like? $\endgroup$ Commented May 19, 2016 at 12:08

1 Answer 1

Reset to default
2
$\begingroup$

What you have, I guess, is DAE in the variable t. If you specify the initial condition g[x, 0] == Cosh[x]/Cosh[Pi], NDSolve will compute a "solution," but warns that "an insufficient number of boundary conditions have been specified for the direction of independent variable x." It then computes different initial values, that lead g to be almost identically zero.

One approach that might work is to differentiate the g-equation with respect to t to get a differential equation (with respect to time). Since we know the initial condition in the OP's example, this is easy to set up. Otherwise, we would have to solve for the IC.

NDSolve[{D[f[x, t], t] == 1 - D[f[x, t], x] g[x, t], D[g[x, t], x, x] == g[x, t] f[x, t], f[x, 0] == 1, f[-π, t] == f[π, t] == 1, g[-π, t] == g[π, t] == 1}, {f, g}, {x, -π, π}, {t, 0, 1}] {sol} = NDSolve[{D[f[x, t], t] == 1 - D[f[x, t], x] g[x, t], D[D[g[x, t], x, x] == g[x, t] f[x, t], t], f[x, 0] == 1, f[-π, t] == f[π, t] == 1, g[x, 0] == Cosh[x]/Cosh[Pi], g[-π, t] == g[π, t] == 1}, {f, g}, {x, -π, π}, {t, 0, 1}];

Result:

GraphicsRow[ Plot3D[Last[#][x, t], {x, -π, π}, {t, 0, 1}, AxesLabel -> Automatic, PlotLabel -> First[#]] & /@ sol ]

Mathematica graphics

The residuals are not very good at the boundaries. I'm not very familiar with PDEs, so I'm not sure what to make of that. It seemed a better solution than f[x, t] = 1+t, g[x, t] = 0 given in the first paragraph above.

GraphicsRow[ Plot3D[Evaluate[# /. sol /. Equal -> Subtract], {x, -π, π}, {t, 0, 1}, AxesLabel -> Automatic, PlotLabel -> #, PlotRange -> All] & /@ {D[f[x, t], t] == 1 - D[f[x, t], x] g[x, t], D[g[x, t], x, x] == g[x, t] f[x, t]} ]

Mathematica graphics

GraphicsRow[ Plot3D[Evaluate[# /. sol /. Equal -> Subtract], {x, -π, π}, {t, 0, 1}, AxesLabel -> Automatic, PlotLabel -> #, PlotRange -> 0.0002] & /@ {D[f[x, t], t] == 1 - D[f[x, t], x] g[x, t], D[g[x, t], x, x] == g[x, t] f[x, t]} ]

Mathematica graphics

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.