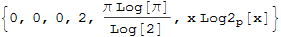3
$\begingroup$

Based on earlier question How to replace the value that include infinity?,

Now, If I have the input A

A= {-3, 0, 1,2}

and do the operation :

B = -Total[(#*Log2[#]& /@ A]

Hence, I do

If[# == 0, 0, # Log2[#]] & /@ A hold = Hold[# Log2[#]] & /@ A ReleaseHold[hold /. HoldPattern[0 Log2[0]] -> 0]

to replace 0.

Now, how can I not enter a negative number in the calculation in B. In other words, B only calculates the positive number and [0 Log2[0]] -> 0.

Thank you very much.

Improve this question
$\endgroup$

4 Answers 4

Reset to default
2
$\begingroup$ 
B = -Total[If[# > 0, (#*Log2[#]), 0] & /@ A]
Improve this answer
$\endgroup$
1
  • $\begingroup$ Thank you for the respond. It try it by puting the given expression in last line and i get {-((3*(I*Pi + Log[3]))/Log[2]), 0, 0, 2} and the answer is -2. the answers is correct, but I want to know, the output of negative value is just expression and not include in calculation right? $\endgroup$ Commented Aug 5, 2016 at 13:45
4
$\begingroup$

For the kind of operation you appear to be doing I typically write a customized function to replace the built-in, here Log2. Basically:

Attributes[pLog2] = Listable; pLog2[x_?NonPositive] := 0 pLog2[x_?NumericQ] := Log2[x] Format[pLog2[x_]] := HoldForm @ Subscript[Log2, p][x]

Now:

#*pLog2[#] & /@ {-3, 0, 1, 2} 
{0, 0, 0, 2}

And also:

#*pLog2[#] & @ {-3, 0, 1, 2, Pi, x}

enter image description here

I included the formatting rule just to illustrate what is possible.

Improve this answer
$\endgroup$
4
  • $\begingroup$ thank you very much for helping me. I already run it but how can I do if I want to substitute the list {-3,0,1,2} as A not the list.? $\endgroup$ Commented Aug 5, 2016 at 13:56
  • 2
    $\begingroup$ @munirah I may misunderstand but I think you mean simply A = {-3, 0, 1, 2} and then on another line -Total[#*pLog2[#] & @ A], or just -Total[A*pLog2[A]]. By the way it is best not to start user Symbol names (like A) with capital letters, as these may conflict with built-ins, e.g. C, D, E, I, N` are all existing reserved Symbols. $\endgroup$ Commented Aug 5, 2016 at 19:05
  • $\begingroup$ It mean when I want to make any, it better for me use small letter?Here, I try to replace the symbol A instead the list {-3, 0, 1, 2} since the list can be variety. hence, I do like this : -Total[#*pLog2[#] & @ A] but iit come error $\endgroup$ Commented Aug 7, 2016 at 0:32
  • 1
    $\begingroup$ @munirah: in short, always use a instead of A, c instead of C, etc. as your variables. $\endgroup$ Commented Aug 7, 2016 at 1:13
4
$\begingroup$

Here is my proposal:

ClearAll[xlgx]; xlgx[x_] := x * Log2[(1 - UnitStep[-x]) (x - 1) + 1];

Or adapting Mr.Wizard's approach, just "truncating" the logarithm:

ClearAll[pLog2]; pLog2[x_] := Log2[(1 - UnitStep[-x]) (x - 1) + 1];

Examples:

OP's:

-Total@xlgx[{-3, 0, 1, 2}] (* -2 *)

Vectorized:

xlgx[Range[-4, 4, 2]] (* {0, 0, 0, 2, 8} *)

Preserves packed arrays (provided output is machine-sized):

xlgx[RandomReal[{-1, 1}, 1000]] // Developer`PackedArrayQ (* True *) xlgx[2^Range[0, 57]] // Developer`PackedArrayQ (* True *)

Valid values:

input = RandomReal[{-1, 10}, 10000]; xlgx[input] == (# Log2[#] /. x_?(Not@*Developer`MachineRealQ) :> 0. & /@ input) (* True *)
Improve this answer
$\endgroup$
3
  • $\begingroup$ Thank you for sharing . i so new in mathematica. I will learn it slowly. It too complex to me to understand $\endgroup$ Commented Aug 5, 2016 at 14:50
  • 2
    $\begingroup$ @munirah Yeah, there is a lot to learn. Fortunately you can still do a lot even with a little knowledge. Try your best to learn on your own using resources like (18), but do not hesitate to ask Questions when you run into trouble. $\endgroup$ Commented Aug 5, 2016 at 19:01
  • $\begingroup$ thank you very much @Mr. Wizard. I learn a lot and improve from this forum. People inside here help me very much. From zero I learn and learn and will learn . $\endgroup$ Commented Aug 7, 2016 at 0:27
0
$\begingroup$ 
a = {-3, 0, 1, 2};

Using ReplaceAt (new in 13.1) and Ramp (new in 11.0)

-Total @ ReplaceAt[x_ :> x*Log2[x], Position[a, _?Positive]] @ Ramp[a]

-2

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.