6
$\begingroup$

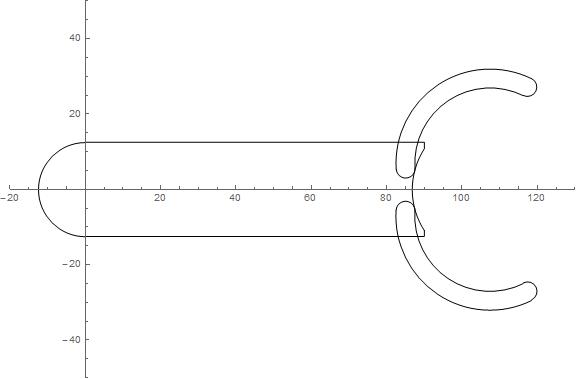
I am trying to tranform an object claw1 to create it mirror image claw2.

I tried using GeometricTransformation, but I did not get works. My code follows. How should I change it?

arm = {Circle[armCenter = {0, 0}, armR = 12.5, {Pi/2, 3*(Pi/2)}], Circle[{106.79, 0}, 20, {2.57, 3.72}], Line[{{0, armR}, {90, armR}, {90, armR}, {90, 10.87}}], Line[{{0, -armR}, {90, -armR}, {90, -armR}, {90, -10.87}}]}; claw1 = {Circle[{106.79, 0}, 20, claw1a = {0.8, 2.89}], Circle[{106.79, 0}, 25, claw1a], Circle[{85, 5.6}, 2.5, claw1b = {2.89, 6.03}], Circle[{122.54, 16.07}, 2.5, claw1c = {0.8, -2.35}]}; claw2 = {Circle[{106.79, 0}, 20, claw1a*-1], Circle[{106.79, 0}, 25, claw1a*-1], Circle[{85, -5.6}, 2.5, claw1b*-1], Circle[{122.54, -16.07}, 2.5, claw1c*-1]}; angClaw1 = GeometricTransformation[ claw1, {RotationTransform[Pi/10, {85, 5.6}]}]; angClaw2 = GeometricTransformation[ claw2, {RotationTransform[-Pi/10, {85, -5.6}]}]; Graphics[{arm, angClaw1, angClaw2}, PlotRange -> {{-20, 130}, {-50, 50}}, Axes -> True, ImageSize -> Large]

enter image description here

Improve this question
$\endgroup$
4
  • $\begingroup$ You can mirror using Scale. Be sure to specify a reference point. Graphics[{Triangle[], Red, Scale[Triangle[], {-1, 1}, {0, 0}]}, Axes -> True]. $\endgroup$ Commented Sep 30, 2016 at 15:16
  • 1
    $\begingroup$ You know what that looks like? $\endgroup$ Commented Sep 30, 2016 at 15:25
  • $\begingroup$ @Szabolcs Would not be {1,-1}? $\endgroup$ Commented Sep 30, 2016 at 16:35
  • 1
    $\begingroup$ @JulienKluge no $\endgroup$ Commented Sep 30, 2016 at 19:19

1 Answer 1

Reset to default
6
$\begingroup$

You can do it with ReflectionTransform. 

claw = {Circle[{106.79, 0}, 20, claw1a = {0.8, 2.89}], Circle[{106.79, 0}, 25, claw1a], Circle[{85, 5.6}, 2.5, claw1b = {2.89, 6.03}], Circle[{122.54, 16.07}, 2.5, claw1c = {0.8, -2.35}]};

The following code demonstrates the two claws rotating.

Manipulate[ Graphics[ {u = GeometricTransformation[claw, {RotationTransform[θ Degree, {85, 5.6}]}], GeometricTransformation[u, ReflectionTransform[{0, 1}, {85, 0}]], Dashed, InfiniteLine[{{0, 0}, {1, 0}}]}, PlotRange -> {{75, 130}, {-45, 45}}, Frame -> True], {u, None}, {θ, -15, 45, 1, Appearance -> "Labeled"}]

Improve this answer
$\endgroup$
1
  • $\begingroup$ I had not asked, but you understood my goal. $\endgroup$ Commented Oct 1, 2016 at 13:54

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.