3
$\begingroup$

I have a solution of Laplace's equation which shows electric potential. I would like to get some data on electric field strength, that is to say a negative gradient of the potential. Here is the code:

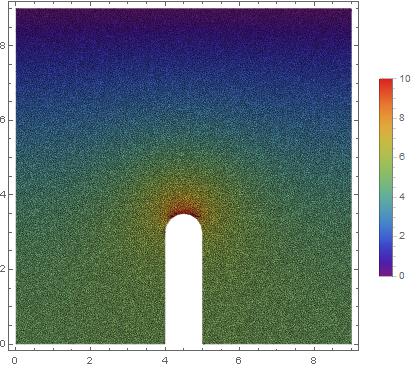
ClearAll["Global`*"] Needs["NDSolve`FEM`"] circle = Disk[{4.5, 3}, 0.5]; pin = Rectangle[{4, 0}, {5, 3}]; square = Rectangle[{0, 0}, {9, 9}]; region = RegionDifference[square, RegionUnion[circle, pin]]; regionplot = RegionPlot[region, PlotTheme -> "Monochrome"]; mesh = ToElementMesh[DiscretizeRegion[region], MaxCellMeasure -> 0.0025 ]; bc = {DirichletCondition[u[x, y] == 0, y == 9], DirichletCondition[u[x, y] == 10, (4.2 <= x <= 4.8) && y <= 4]}; sol = NDSolveValue[{D[u[x, y], x, x] + D[u[x, y], y, y] == 0 , bc}, u, {x, y} \[Element] mesh]; DensityPlot[sol[x, y], {x, y} \[Element] mesh, Mesh -> All, ColorFunction -> "Rainbow", PlotRange -> All, PlotLegends -> Automatic]

DensityPlot looks like this:

densityplot

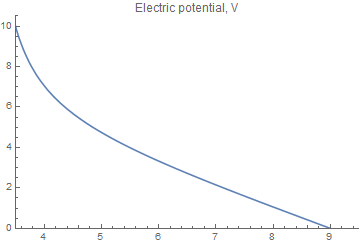
Now I am looking at the very top of the semicircular area where u[x,y]==10. I want a plot of the potential along the center line (x==4.5 and 3.5 =< y <= 9), so I do this:

Plot[sol[4.5, x], {x, 3.5, 9}, PlotRange -> {{3.5, 9.5}, {0, 10.5}} , AxesOrigin -> {3.5, 0}, PlotLabel -> "Electric potential, V"]

The result is this:

potential

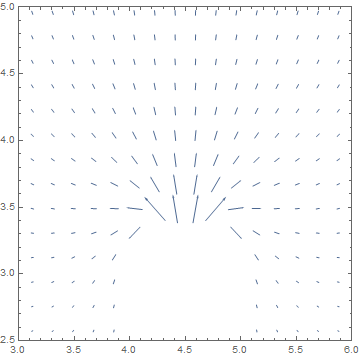
Now I would like to see what the negative gradient of u[x,y] is like for the same x==4.5 and 3.5 =< y <= 9. For that I do:

electricField = -Grad[sol[x, y], {x, y}]; VectorPlot[electricField, {x, y} \[Element] mesh, PlotRange -> {{3, 6}, {2.5, 5}}, VectorPoints -> 50]

Setting PlotRange to zoom in to the top of the semicircle gives this plot:

vectorfield

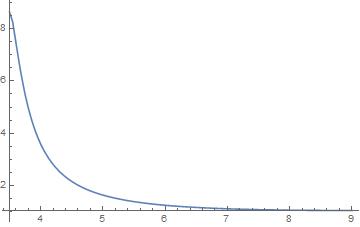
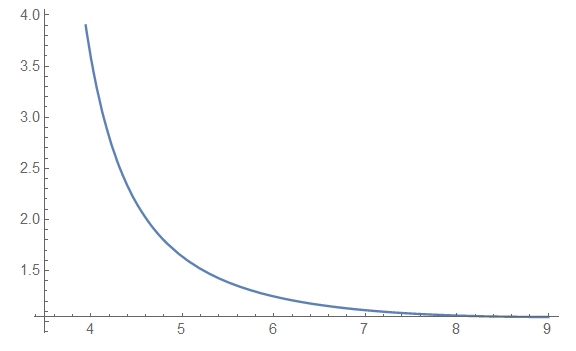
And finally I ran into a problem. I would like to plot a magnitude of the electric field along the center line (x==4.5 and 3.5 =< y <= 9) just like I did with the electric potential. How do I do this? I suppose I can either extract it from -Grad[sol[x, y], {x, y}] or from the plot of electric potential.

This question is related to this post. I used Mathematica 10.3.

Improve this question
$\endgroup$
0

2 Answers 2

Reset to default
3
$\begingroup$

It can also be done like this,

mef[x_, y_] = -Grad[sol[x, y], {x, y}]; Plot[mef[4.5, y][[2]], {y, 3.5, 9}, PlotRange -> Full]

Much faster!

enter image description here

Improve this answer
$\endgroup$
0
2
$\begingroup$

Try this:

 Plot[Evaluate[ Sqrt[D[sol[x, y], x]^2 + D[sol[x, y], y]^2] /. x -> 4.5], {y, 3.5, 9}]

enter image description here

Have fun!

Improve this answer
$\endgroup$
2
  • $\begingroup$ Thanks for your help! Instead of using any built-in function you calculate the magnitude of the vector field for x -> 4.5 on your own. I like it! However, there is one problem. It works only partly. The semicircle starts at y == 3.5. And in the plot that you provided all results between y == 3.5 and y== 4.0 are missing. They are the most important ones since that's where the strength of the field is the highest. Any suggestion on getting these values? Also, in my Mathematica 10.3 I had to add AxesOrigin -> {3.5, 0} to get the same plot as yours. $\endgroup$ Commented Apr 28, 2017 at 20:01
  • $\begingroup$ Never mind. It works perfectly. We just have to add PlotRange -> Full. Thanks again! $\endgroup$ Commented Apr 28, 2017 at 23:52

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.