7
$\begingroup$

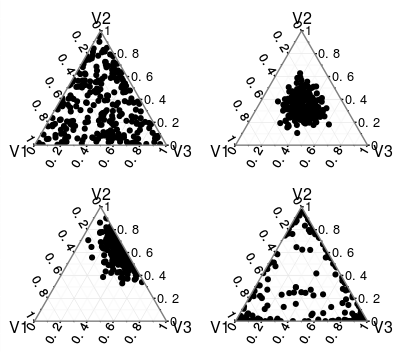
I'm wondering if there's something in Mathematica similar to the built-in function in R shown in the figures below, borrowed from this post, possibly with flexible axes "orientation", ticksmarks, tick numbers, and gridlines.

enter image description here

By a 3-category Dirichlet distribution, it means that each data point is in the form of $\{u, v, 1-u-v\}$, where the degree of freedom is two with $0<u<1$, $0<v<1$, and $0<u+v<1$.

Currently I've been doing something like the demonstrative code below, transforming the data points myself from $\{u,v\}$ in the usual Cartesian coordinates to the "triangular" coordinates. (here the "vertical" axis is flipped just like those plots from R)

ClearAll[Opt, data, dN]; dN = 100; data = RandomReal[{0, 1}, {dN, 3}]; data = data/(Total /@ data); Opt = {PlotStyle -> PointSize -> Medium, AspectRatio -> 1, PlotRange -> {{0, 1}, {0, 1}}, GridLines -> {{1}, {1}} }; GraphicsRow[{ListPlot[data[[;; , 1 ;; 2]], Epilog -> Line@{{1, 0}, {0, 1}}, Evaluate@Opt] , ListPlot[ Thread@{1/2 (1 + data[[;; , 1]] - data[[;; , 2]]), Sqrt[3] data[[;; , 3]]/2} , Epilog -> {FaceForm[], EdgeForm@[email protected], Triangle@{{0, 0}, {1, Sqrt[3]}/2, {1, 0}}}, Evaluate@Opt]}, ImageSize -> 500]

enter image description here

Firstly I feel kind of stupid having to do it this way every time. Secondly, it's tedious to add the tickmarks, gridlines, etc.

So, repeating my question statement in the opening line:

Is there actually a similar built-in graphics package in MMA? If not, is there a convenient way to achieve some if not all the features in a "triangular plot" shown in the R plots?

I would imagine that Dirichlet distribution is pretty common and someone have developed something practically useful already.

Pointers to references or any suggestions will be appreciated.

Improve this question
$\endgroup$
4
  • 1
    $\begingroup$ Would you be opposed to using the native R package from within Mathematica through RLink? $\endgroup$ Commented May 2, 2018 at 15:03
  • $\begingroup$ @MarcoB oh thank you for reminding me of that. I wouldn't really mind using RLink, however, I prefer the style of the graphics primitives in MMA. It's also about consistency, it feels a bit weird seeing an R plot among other MMA plots, either in formal or informal presentation. $\endgroup$ Commented May 2, 2018 at 15:13
  • 2
    $\begingroup$ Have you seen How to plot ternary density plots? You might be interested in other posts on ternary plots. $\endgroup$ Commented May 2, 2018 at 15:56
  • $\begingroup$ @MarcoB These posts and in fact just the term "ternary plot" is very helpful. Thank you so much. $\endgroup$ Commented May 3, 2018 at 0:45

1 Answer 1

Reset to default
5
$\begingroup$

How is this? It does not support all Graphics options, but that can be customized. As is, it mimics the styling of ListPlot.

ClearAll[BarycentricPlot]; BarycentricPlot[data_?MatrixQ, OptionsPattern[{ "Ticks" -> N@Range[0, 1, 1/10] }]] := Module[{λ, pts, plot, h, c, opts, g, s, prolog, gridlinesx, gridlinesy, ticks}, h = Sin[Pi/3]; c = {1/2, h/3}; λ = data/Total[data, {2}]; plot = ListPlot[λ.Developer`ToPackedArray[ N[{{0, 0}, {1, 0}, {1/2, h}}]]]; opts = Options[plot]; ticks = OptionValue["Ticks"]; gridlinesy = ticks[[2 ;; -2]] h; gridlinesx = gridlinesy/Tan[Pi/3]; g[label_, θ_, ϕ_] := Graphics[{ Rotate[ Text[Style[label, {}], {1/2, h + 0.1}], ϕ, {1/2, h + 0.1}], GridLinesStyle /. opts, Line@Transpose[{ Transpose[{gridlinesx , gridlinesy}], Transpose[{1 - gridlinesx , gridlinesy}] }] }, PlotRangePadding -> 0, ImageMargins -> 0.1, PlotRange -> {{0, 1}, {0, 2 h}}, Axes -> {True, False}, Ticks -> {Table[{x, Rotate[x, 4 Pi/3 + θ]}, {x, ticks}], None}, AxesStyle -> (AxesStyle /. opts) ]; s = 1.055; prolog = Graphics[{ Inset[g["\!\(\*SubscriptBox[\(μ\), \(3\)]\)", -Pi, 0], c, c, s], Rotate[ Inset[g["\!\(\*SubscriptBox[\(μ\), \(1\)]\)", 0, Pi], c, c, s], 2/3 Pi, c], Rotate[ Inset[g["\!\(\*SubscriptBox[\(μ\), \(2\)]\)", -Pi, -Pi], c, c, s], 4/3 Pi, c] }, PlotRange -> {{0, 1}, {0, h}}, PlotRangePadding -> Scaled[0.15], Frame -> False ]; Show[{prolog, plot}] ] dN = 1000; data = RandomReal[{0, 1}, {dN, 3}]; BarycentricPlot[data]

enter image description here

Improve this answer
$\endgroup$
1
  • $\begingroup$ It looks great! I will need some time to get familiar with part of the construct that is more advanced (to me). Really appreciated your demonstration of good coding practice. $\endgroup$ Commented May 3, 2018 at 0:53

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.