4
$\begingroup$

Mathematica will not, in general, do arbitrary order interpolation on unstructured grids:

<< NDSolve`FEM` f[x_, y_] := (1 - x^2 + y^2); mesh = ToElementMesh[Disk[]]; coords = mesh["Coordinates"]; vals = f @@ # & /@ coords; if = Interpolation[MapThread[{#1, #2} &, {coords, vals}], InterpolationOrder -> 2]

results in a message saying Interpolation::udeg: Interpolation on unstructured grids is currently only supported for InterpolationOrder->1 or InterpolationOrder->All. Order will be reduced to 1.

On the other hand if I use ElementMeshInterpolation:

emif2 = ElementMeshInterpolation[{mesh}, vals, InterpolationOrder -> 2]

It seems to have no problem. It also seems to only actually give the first order interpolation no matter what I specify. If I plot the difference between Interpolation and ElementMeshInterpolation run at first and second order I get identical plots.

if1 = Interpolation[MapThread[{#1, #2} &, {coords, vals}], InterpolationOrder -> 1] emif1 = ElementMeshInterpolation[{mesh}, vals, InterpolationOrder -> 1] emif2 = ElementMeshInterpolation[{mesh}, vals, InterpolationOrder -> 2] GraphicsGrid[{{ContourPlot[emif1[x, y] - if1[x, y], {x, y} \[Element] Disk[]], ContourPlot[emif2[x, y] - if1[x, y], {x, y} \[Element] Disk[]]}}]

enter image description here

Is ElementMeshInterpolation silently falling back to 1st order? Is there any way to get higher order interpolations on an unstructured grid?

Improve this question
$\endgroup$
1
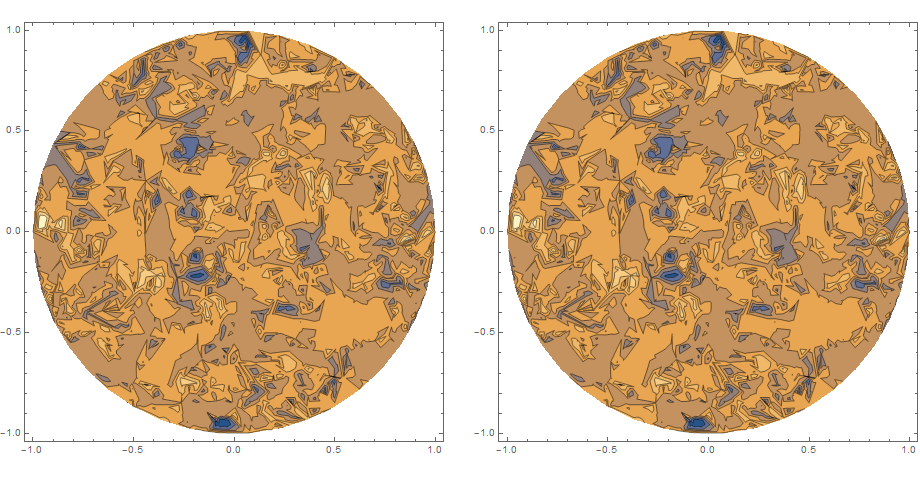
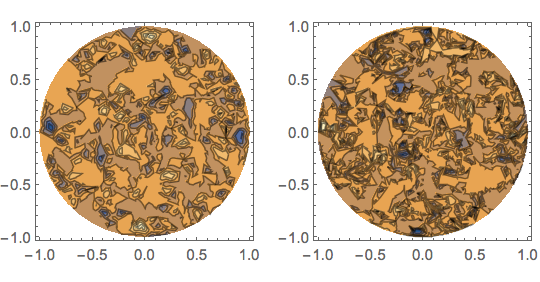
  • $\begingroup$ if you generally mean "arbitrary," then, no, the interpolation order can only be 1 or 2, and it depends on the order of the underlying mesh. OTOH, your example seems to raise a more particular question. $\endgroup$ Commented Aug 24, 2018 at 1:11

1 Answer 1

Reset to default
4
$\begingroup$

ElementMeshInterpolation seems to default to the order of the underlying mesh, which is 2 in the example. Alter the order of mesh to get an order 1 mesh & interpolation, and you can construct two different interpolations.

mesh1 = MeshOrderAlteration[mesh, 1]; vals1 = f @@@ mesh1["Coordinates"]; if1 = Interpolation[MapThread[{##} &, {coords, vals}], InterpolationOrder -> 1]; emif1 = ElementMeshInterpolation[{mesh1}, vals1, InterpolationOrder -> 1]; emif2 = ElementMeshInterpolation[{mesh}, vals, InterpolationOrder -> 2]; GraphicsGrid[{{ContourPlot[ emif1[x, y] - if1[x, y], {x, y} \[Element] Disk[]], ContourPlot[emif2[x, y] - if1[x, y], {x, y} \[Element] Disk[]]}}]

Mathematica graphics

Improve this answer
$\endgroup$
1
  • $\begingroup$ You may want to compare emif1 and emif2 with if1 = Interpolation[MapThread[{##} &, {mesh1["Coordinates"], vals1}], InterpolationOrder -> 1]. For some reason, I didn't grok the purpose of the plots at first. $\endgroup$ Commented Aug 24, 2018 at 12:41

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.