16
$\begingroup$

Given a directed acyclic graph, there is always a possibility to plot the graph as layers, where nodes always send edges into one direction (usually down), to successive layers, and never backwards. The "LayeredDrawing" option value for GraphLayout fails miserably. There is the built-in (but somewhat obsolete) LayeredGraphPlot, which can do this, but it is obviously not part of the new Graph-paradigm. What would be an efficient and elegant algorithm to lay such a graph in 2D?

Row@{ Graph[{1 -> 2, 1 -> 3, 2 -> 3, 1 -> 4, 2 -> 4, 1 -> 5}, ImageSize -> 200, VertexLabels -> (# -> # & /@ Range@5), GraphLayout -> "LayeredDrawing", ImagePadding -> 10], LayeredGraphPlot[{1 -> 2, 1 -> 3, 2 -> 3, 1 -> 4, 2 -> 4, 1 -> 5}, VertexLabeling -> True, ImageSize -> 200] }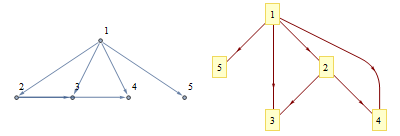

Mathematica graphics

Note, that while TopologicalSort gives a top-down sorting of vertices, usually there are multiple solutions for topological sorting, thus multiple ways to layer the same graph. Also, the algorithm must take into account that not all children of a parent should end up on the same layer (see e.g. vertex 1 in the right plot). A nice algorithm for laying out arrows is welcome as well.

Improve this question
$\endgroup$
4
  • 2
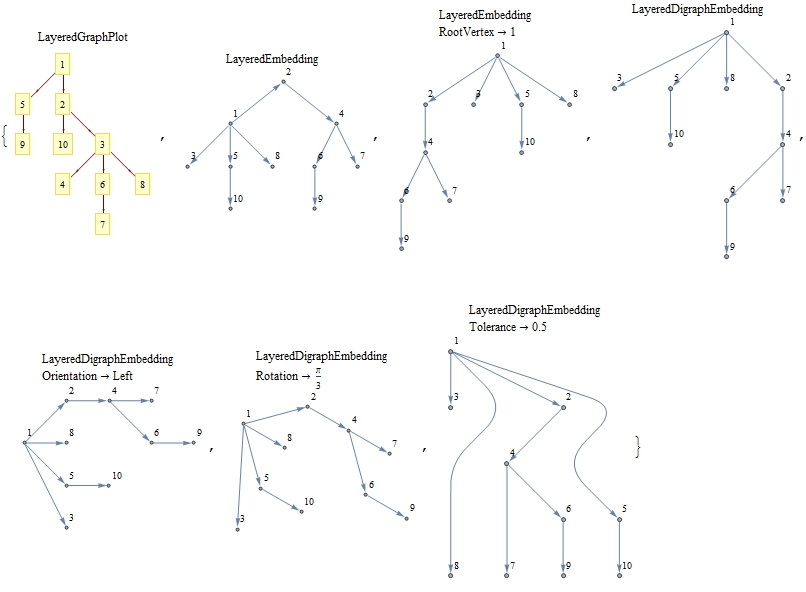
    $\begingroup$ I use LayeredGraphPlot. It helps to compute the transitive reduction of your graph first (if you want to draw all the edges, pick off the vertex coordinates from the layered plot of the transitive reduction and then plot the full graph). Transitive reduction was implemented in Combinatorica, but it's not included for Mathematica 8 Graph objects. Fortunately, they give you TopologicalSort, so it's fairly easy to implement. $\endgroup$ Commented Feb 16, 2012 at 1:10
  • 4
    $\begingroup$ I should add that LayeredGraphPlot does, in fact, work with Mathematica 8 native Graph objects. $\endgroup$ Commented Feb 16, 2012 at 2:52
  • 1
    $\begingroup$ GraphPlot and related functions are far from obsolete in v8. Graph can't do everything they can (e.g. multigraphs). Graph drawing is complex enough to be a research field on its own so I am not sure if it's worthwhile trying to implement your own algorithm for this. $\endgroup$ Commented Feb 16, 2012 at 7:52
  • $\begingroup$ did you see stackoverflow.com/questions/4245946/…. It converts the layout of the old graph towards the new graph? $\endgroup$ Commented Feb 16, 2012 at 10:15

3 Answers 3

Reset to default
11
$\begingroup$

I was about to give this a second go and implement a layout algorithm manually based on Szabolcs's answer, when I realized that since v9, we have built-in options to lay out trees and directed acyclic graphs in the above specified layered way:

SetOptions[Graph, VertexLabels -> "Name", ImagePadding -> 10]; edges = {1 -> 2, 1 -> 3, 1 -> 5, 1 -> 8, 2 -> 4, 4 -> 6, 4 -> 7, 5 -> 10, 6 -> 9}; Prepend[ Graph[edges, GraphLayout -> #, PlotLabel -> If[ListQ@#, Column@#, #]] & /@ { "LayeredEmbedding", {"LayeredEmbedding", "RootVertex" -> 1}, "LayeredDigraphEmbedding", {"LayeredDigraphEmbedding", "Orientation" -> Left}, {"LayeredDigraphEmbedding", "Tolerance" -> .5}}, LayeredGraphPlot[edges, Top, VertexLabeling -> True, PlotLabel -> "LayeredGraphPlot"]]

enter image description here

Note that simple "LayeredEmbedding" still produces the wrong layout (1 is below 2), but now a "RootVertex" option can specify the root node. I've included LayeredGraphPlot for comparison. "LayeredDigraphEmbedding" was specifically added in v9 for directed acyclic graphs. Its submethod options can be used to tweak the position of the root, orientation and the tolerance used in terminating the energy minimization process.

One could get the vertex coordinates as follows:

coord = {}; Graph[edges, GraphLayout -> "LayeredDigraphEmbedding", VertexShapeFunction -> (Disk[AppendTo[coord, #2 -> #1]; #1, .1] &)] coord 
{1 -> {0., 4.}, 2 -> {1., 3.}, 3 -> {-2., 3.}, 5 -> {-1., 3.}, 8 -> {0., 3.}, 4 -> {1., 2.}, 6 -> {0., 1.}, 7 -> {1., 1.}, 10 -> {-1., 2.}, 9 -> {0., 0.}}

Check out the GraphLayout option because it contains some more layout methods in v9!

Improve this answer
$\endgroup$
5
$\begingroup$

Note: I am assuming that you are interested in coming up with a layout algorithm, and not just getting a pretty plot with whatever Mathematica has built in.

I will admit right now that I do not know how this is usually done, but here's a naive idea for a starting point:

Let's put vertex $v$ on layer number $n$ if $n$ is the maximal distance of $v$ from any other vertex. This will not give the same thing as LayeredGraphPlot, but it's a good approximation. Here's an implementation:

amat = AdjacencyMatrix[graph]; paths = NestWhileList[amat.# &, amat, Total[#, 2] > 0 &]; layers = Max /@ Transpose@Total@Clip@Accumulate@Reverse[paths]; SortBy[Thread[VertexList[graph] -> layers], Last]

It will return a list of the form vertex -> layerNumber.

It is based on the observation that if $A$ is the adjacency matrix, then $(A^k)_{ij}$ will give the number of paths of length $k$ from vertex $i$ to vertex $j$.

Improve this answer
$\endgroup$
4
$\begingroup$

Use this answer by Yaroslav Bulatov.

test = LayeredGraphPlot[{1 -> 2, 1 -> 3, 2 -> 3, 1 -> 4, 2 -> 4, 1 -> 5}, VertexLabeling -> True, ImageSize -> 200] getLabelCoordinateMap[gp1_] := Module[{points, labels, actualLabels, coordAliases, actualCoords}, points = Cases[gp1, GraphicsComplex[points_, __] :> points, Infinity] // First; labels = Cases[gp1, Text[___], Infinity]; actualLabels = labels[[All, 1, 1]]; coordAliases = labels[[All, 2]]; actualCoords = points[[coordAliases]]; Thread[actualLabels -> actualCoords]]; coord = getLabelCoordinateMap[test] Graph[{1 -> 2, 1 -> 3, 2 -> 3, 1 -> 4, 2 -> 4, 1 -> 5}, ImageSize -> 200, VertexLabels -> (# -> # & /@ Range@5), VertexCoordinates -> coord, ImagePadding -> 10]

It gives the following:

Mathematica graphics

Improve this answer
$\endgroup$
1
  • $\begingroup$ The problem with this method is twofold: first, I have to run LayeredGraphPlot, which involves a lot of unnecessary computation (I assume), and second, I still don't have a layering algorithm. $\endgroup$ Commented Feb 21, 2012 at 11:50

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.