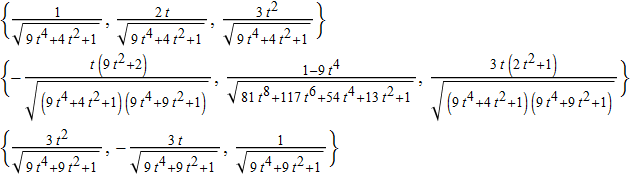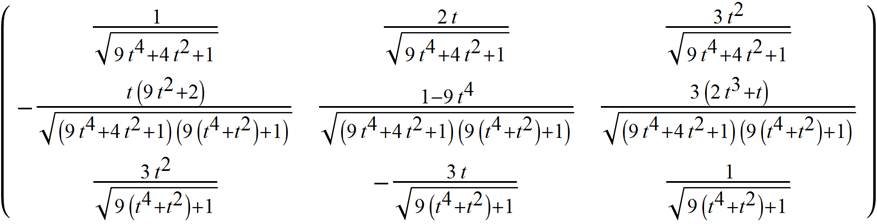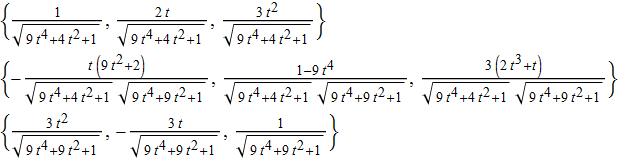33
$\begingroup$

For my Calc III class, I need to find $T(t), N(t)$, and $B(t)$ for $t=1, 2$, and $-1$, given $r(t)=\{t,t^2,t^3\}$.

I've got Mathematica, but I've never used it before and I'm not sure how to coerce it into solving this. (My professor told us to use a computer, as it starts getting pretty nasty around $T'(t)$. By hand, $$T(t)=\frac{1}{ \sqrt{(1+4t^2+9t^4})}\{1,2t,3t^2\}$$

I've tried defining r as stated above and using D,Norm, and CrossProduct.

However, I get a bunch of Abs in my outputs (am I missing an assumption?). Additionally, I can't seem to google up how to ask Mathematica to sub in a specific value for $t$, once I get the equations worked out properly.

Improve this question
$\endgroup$
1
  • 1
    $\begingroup$ Welcome to Mathematica.SE! I have formatted some code for you. This page explains how to do it. You might want to consider a more memorable username? Also, if you register your account, any reputation points you get on this or subsequent questions or answers will cumulate, no matter where you log in from. $\endgroup$ Commented Jan 28, 2013 at 11:42

4 Answers 4

Reset to default
48
$\begingroup$

Mathematica wouldn't be much helpful if one applied only formulae calculated by hand.
Here we demonstrate how to calculate the desired geometric objects with the system having a definition of the curve r[t] :

r[t_] := {t, t^2, t^3}

now we call uT the unit tangent vector to r[t]. Since we'd like it only for real parameters we add an assumption to Simplify that t is a real number. Similarly we can do it for the normal vector vN[t] and the binormal vB[t] :

uT[t_] = Simplify[ r'[t] / Norm[ r'[t] ], t ∈ Reals]; vN[t_] = Simplify[ uT'[t]/ Norm[ uT'[t]], t ∈ Reals]; vB[t_] = Simplify[ Cross[r'[t], r''[t]] / Norm[ Cross[r'[t], r''[t]] ], t ∈ Reals];

let's write down the formulae :

{uT[t], vN[t], vB[t]} // Column // TraditionalForm

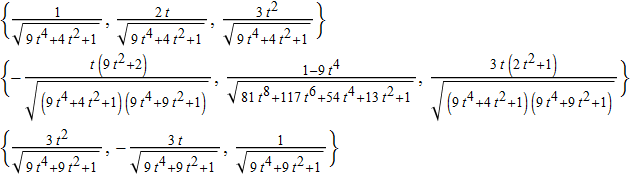
enter image description here

Edit

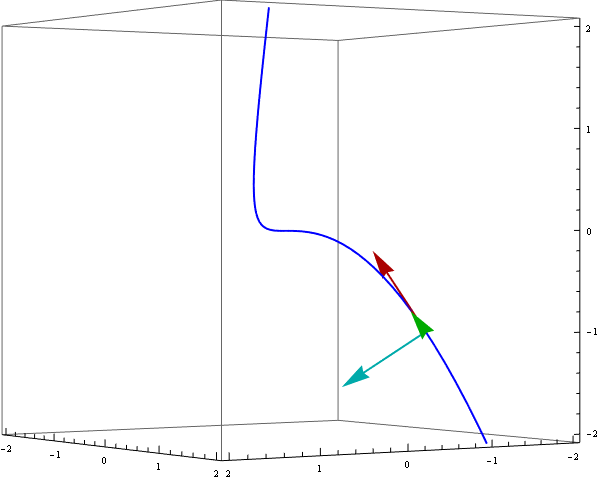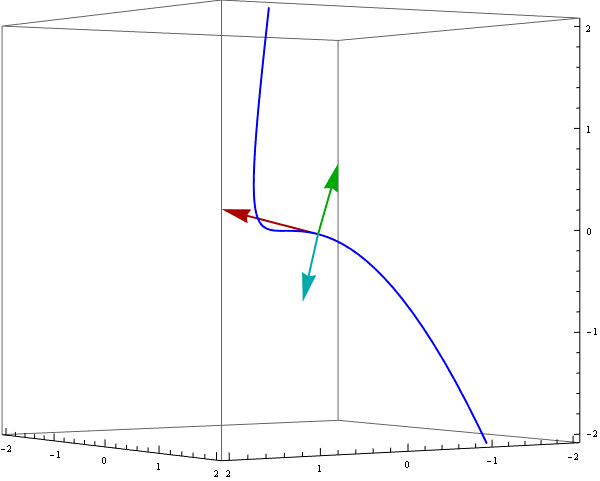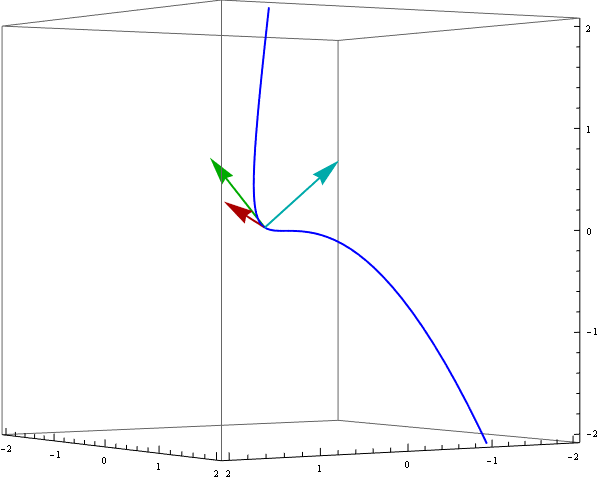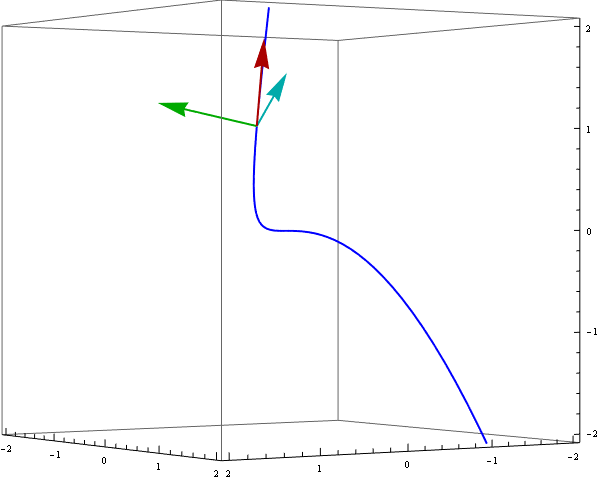
Definitions provided above are clearly more useful than only to write them down. They are powerful enough to animate a moving reper along a curve r[t]. Indeed the vectors uT[t], vN[t] and vB[t] are orthogonal and normalized, e.g. 

Simplify[ Norm /@ {uT[t], vN[t], vB[t]}, t ∈ Reals] 
 {1, 1, 1}

To demonstrate a moving reper we can use ParametricPlot3D and Arrow enclosed in Animate : 

Animate[ Show[ ParametricPlot3D[ {r[t]}, {t, -1.3, 1.3}, PlotStyle -> {Blue, Thick}], Graphics3D[{ {Thick, Darker @ Red, Arrow[{r[s], r[s] + uT[s]}]}, {Thick, Darker @ Green, Arrow[{r[s], r[s] + vB[s]}]}, {Thick, Darker @ Cyan, Arrow[{r[s], r[s] + vN[s]}]}}], PlotRange -> {{-2, 2}, {-2, 2}, {-2, 2}}, ViewPoint -> {4, 6, 0}, ImageSize -> 600], {s, -1, 1}]

enter image description here

Improve this answer
$\endgroup$
7
  • 2
    $\begingroup$ This produces the same answers I ended up with before (which is good!), and is much, much cleaner. Thanks very much! $\endgroup$ Commented Jan 28, 2013 at 13:13
  • 4
    $\begingroup$ Wouldn't it normally be better to define uT, vN and vB using Set instead of SetDelayed, so Simplify only gets called when the functions are declared, not every time they're called? $\endgroup$ Commented Jan 28, 2013 at 13:13
  • 1
    $\begingroup$ @nikie Assuming more general parametrizations of the curve than simply t -> r[t] then it would be better, but to be consequent one should define uT this way uT[c_Symbol,t_]. $\endgroup$ Commented Jan 28, 2013 at 13:46
  • 2
    $\begingroup$ I'm not sure I can follow you. What I meant was using uT[t_] = ... instead of uT[t_] := .... Because right now, if I used e.g. Plot[uT[t], {t,...}], Simplify would be called every time uT is evaluated. $\endgroup$ Commented Jan 28, 2013 at 14:53
  • 6
    $\begingroup$ +1 Beautifully done. One minor suggestion: the frame makes more sense when the curve is parameterized by arclength; it should then be moving along at a constant speed. @wxffles: "reper" surely is a shorthand for the French "repere mobile" (please pardon the lack of accents on this keyboard), which usually is translated "moving frame." Its use goes back at least to Elie Cartan who made notable use of moving frames in his geometric investigations around 1900-1930. $\endgroup$ Commented Jan 28, 2013 at 22:33
14
$\begingroup$

Observe that even when the tangent vector $r'(t)$ is not normalized, it is still a linear combination of $T(t)$ and $N(t)$. Thus--operating under the usual assumptions that $r'$ and $r''$ exist and are linearly independent--all we have to do is make an orthonormal frame out of $r'(t)$ and $r''(t)$ (which is very much in the spirit of the entire proceeding). It often helps to do the simplification on the spot, so let's include that too. In the following, the calculation itself is the middle line, enclosed by the simplification code:

frame[r_] := Function[{t}, Evaluate[FullSimplify[ Append[#, Cross @@ #] &@ Orthogonalize[D[r[t], {t, #}] & /@ {1, 2}, Dot], Assumptions -> t ∈ Reals]]]

(If you read the second line in reverse you can tell exactly what it does: take the first two derivatives, orthogonalize them, and throw in their cross product. Including Dot as an option to Orthogonalize does not change the calculation but makes it much easier for Mathematica to simplify the ensuing expressions.)

This object frame transforms any twice-differentiable 3-vector-valued function into a frame-valued function, which returns a list of three 3-vectors; namely, the unit tangent, normal and binormal $\{T(t), N(t), B(t)\}$. For instance, the example in the question can now be addressed by

frame[{#, #^2, #^3} &][t] // TraditionalForm

Output

The method used in frame generalizes to higher (and lower) dimensions: sequentially orthogonalize the first $n-1$ derivatives (in order) and use the wedge product (a generalization of Cross) to obtain the last element of the frame. The wedge product (which is applied to an ordered list of $n-1$ $n$-vectors) can be implemented as Dot[LeviCivitaTensor[Length[#]+1], Sequence @@ #]&.

Improve this answer
$\endgroup$
13
$\begingroup$

Mathematica 10 provides new functionality dealing with curves, (see e.g. the Vector Analysis tutorial) like ArcLength, ArcCurvature and especially FrenetSerretSystem:

FrenetSerretSystem[{ x1, ..., xn}, t] gives the generalized curvatures and Frenet-Serret basis for the parametric curve x[t] i.e. it returns {{ k1, ..., k(n-1)}, { e1, ..., en}}, where ki are generalized curvatures and ei are the Frenet-Serret basis vectors.

Symbolically it yields

 FrenetSerretSystem[ r[t], t] // TraditionalForm

enter image description here

Since we are interested in the Frenet-Seret basis only, having defined

r[t_] := {t, t^2, t^3}

we can evaluate:

FrenetSerretSystem[ r[t], t] // Last // Simplify // Column // TraditionalForm

enter image description here

With FrenetSerretSystem we don't need to define every base vector separately and we can use it also in animations like in the accepted answer.

Improve this answer
$\endgroup$
2
  • 1
    $\begingroup$ The new FrenetSerretSystem perfectly illustrates how adding certain higher-level functions to Mathematica in part impedes the pedagogical opportunity to learn such higher-level mathematical constructs by building them up from lower-level ones. (Of course one may still "simulate" such a function by building it up.) Another, much older example: RowReduce. $\endgroup$ Commented Aug 2, 2014 at 20:07
  • 4
    $\begingroup$ @murray But on the other hand, once you understand the procedure, I think you'd want a convenient way to access it - and therefore having it available in canned form is good, instead of making your own library. $\endgroup$ Commented Aug 3, 2014 at 21:54
8
$\begingroup$

This is mainly an answer to your last question, but I think it will help with your other ones. I assume you know that the $T$ function is vector valued, and that is what you want.

To substitute in a specific value of $t$, you probably want replacement rules, specifically the ReplaceAll (/.) construct.

For example, if you had defined your expression $T(t)$ as 

bigT={1,2t,3t^2}/Sqrt[1+4 t^2+9 t^4]

(I called it bigT because it is not good practice to name expressions as single capital letters, in case they clash with a built in definition.) Then you would type

 bigT/. t-> 2

Or whatever the desired value might be.

The other way to go would be to define a function using SetDelayed. Then it doesn't actually have to be t as the argument. Notice the underscore (Blank) to denote a pattern.

BigTFunction[x_]:= {1,2x,3x^2}/Sqrt[1+4 x^2+9 x^4] BigTFunction[2]
Improve this answer
$\endgroup$
4
  • $\begingroup$ That's exactly what I was looking for; thanks very much! $\endgroup$ Commented Jan 28, 2013 at 11:46
  • $\begingroup$ You are most welcome. Don't rush to do this, in case you get a better answer from someone else, but it is good practice to mark the best answer you receive as "accepted" by clicking the checkmark next to it. $\endgroup$ Commented Jan 28, 2013 at 11:48
  • $\begingroup$ I'll keep that in mind! You've already helped a lot, but my remaining question, then, I suppose, is concerning N(t): simply taking bigN=D[bigT,t]/Norm[D[bigT,t]] outputs a massive jumble of fractions and roots interspersed with Abs values. Replacing t->1 and passing it through FullSimplify gives a reasonable seeming answer, but I don't have any way of knowing if I can trust it. The same goes for B(t), except that it of course is Cross[bigT,bigN]. Thanks much again, either way! $\endgroup$ Commented Jan 28, 2013 at 11:57
  • $\begingroup$ Try substituting a real number 1. instead of exact value integer 1; another thing you can try is plotting the expression. $\endgroup$ Commented Jan 28, 2013 at 12:12

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.