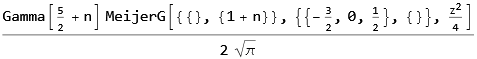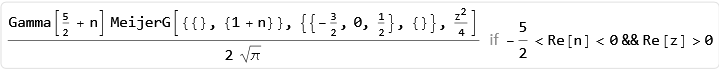4
$\begingroup$

I have an integral of general form

$$ i_n(z)=\dfrac{z^2}{K_2(z)}\int_1^{\infty} \dfrac{\left(x^2-1\right)^{n+\frac{3}{2}}}{x^{2n+1}} \exp(-zx) dx $$

$K_2(z)$ is the bessel function and $0.01 \leqslant z\leqslant 1000$.

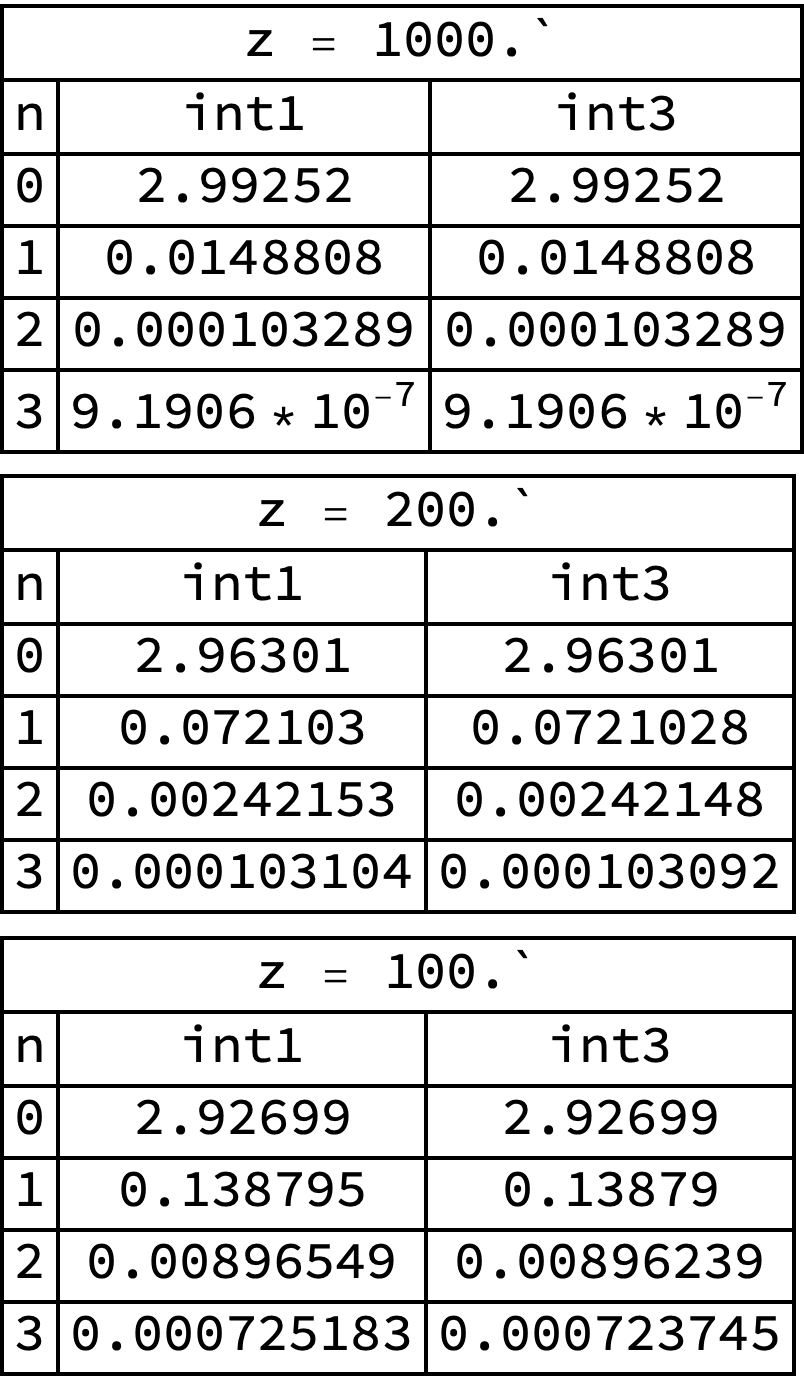
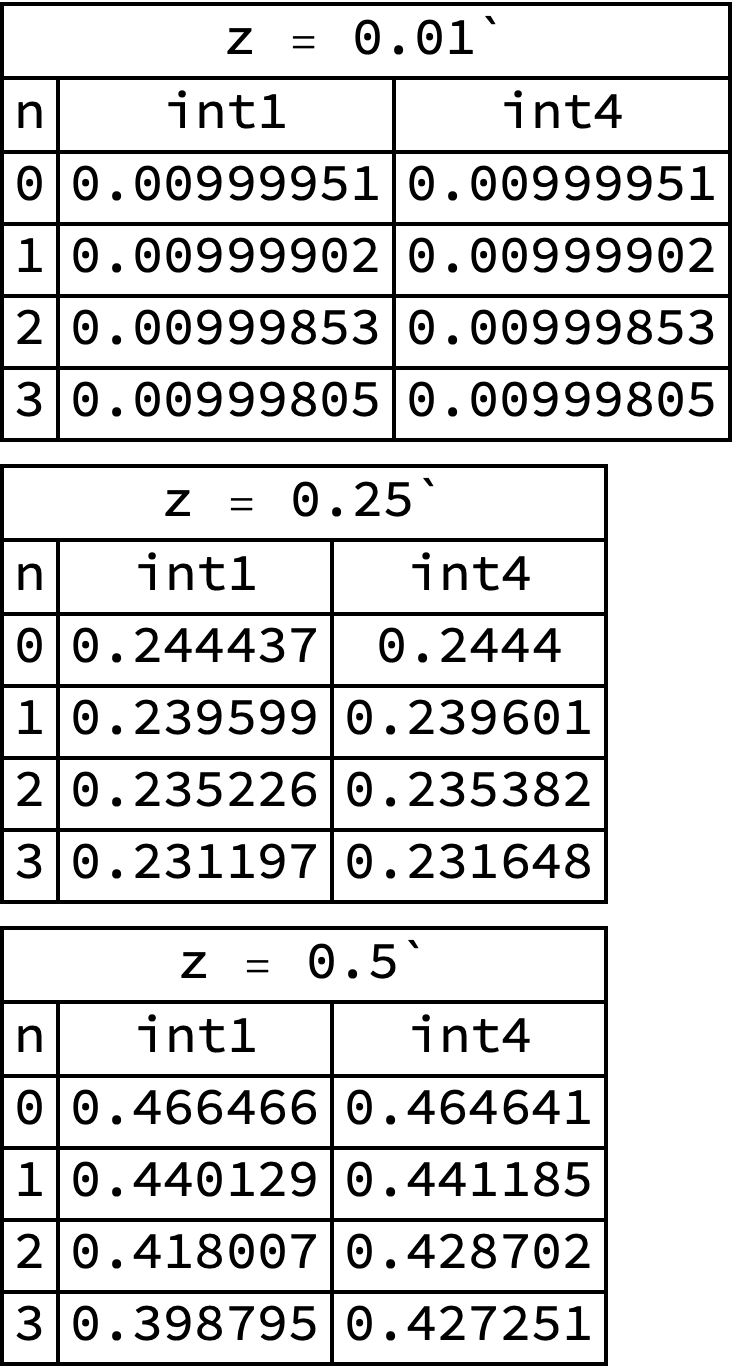
in[z_]:= Assuming[Re[z]>0,(z^2/BesselK[2,z]) NIntegrate[((x^2-1)^(n+(3/2))/x^(2n+1)) Exp[-z x],{x,1,Infinity},WorkingPrecision -> $MachinePrecision,AccuracyGoal -> 3]]

For reasons of analytical calculation, I would like to get symbolically the first four integrals $i_0$, $i_1$, $i_2$ and $i_3$ but MATHEMATICA does not do this. Do you have an idea please?

(* i0 *) i0[z_]:= Assuming[Re[z]>0,(z^2/BesselK[2,z]) NIntegrate[((x^2-1)^(3/2)/x) Exp[-z x],{x,1,Infinity},WorkingPrecision -> $MachinePrecision,AccuracyGoal -> 3]] (* i1 *) i1[z_]:= Assuming[Re[z]>0,(z^2/BesselK[2,z]) NIntegrate[((x^2-1)^(5/2)/x^3) Exp[-z x],{x,1,Infinity},WorkingPrecision ->$MachinePrecision,AccuracyGoal -> 3]] (* i2 *) i2[z_]:= Assuming[Re[z]>0,(z^2/BesselK[2,z]) NIntegrate[((x^2-1)^(7/2)/x^5) Exp[-z x],{x,1,Infinity},WorkingPrecision ->$MachinePrecision,AccuracyGoal -> 3]] (* i3 *) i3[z_]:= Assuming[Re[z]>0,(z^2/BesselK[2,z]) NIntegrate[((x^2-1)^(9/2)/x^7) Exp[-z x],{x,1,Infinity},WorkingPrecision ->$MachinePrecision,AccuracyGoal -> 3]]

Alternatively, can these four integrals be expressed numerically as a fite for $z$ values between 0.01 and 1000?

Thank you in advance!

Improve this question
$\endgroup$
1
  • 3
    $\begingroup$ Hi. Just wanted to say that I think you should not have mentioned $z^2/K_2(z)$ at all here, it is irrelevant for your question. $\endgroup$ Commented Oct 2, 2022 at 5:47

2 Answers 2

Reset to default
6
$\begingroup$ 
$Version (* "13.1.0 for Mac OS X x86 (64-bit) (June 16, 2022)" *) Clear["Global`*"] int1[n_Integer?NonNegative][z_] = Assuming[ Re[z] > 0 && Element[n, NonNegativeIntegers], (z^2/BesselK[2, z])*Integrate[ ((x^2 - 1)^(n + (3/2))/x^(2 n + 1)) Exp[-z*x], {x, 1, Infinity}]] (* (2 Gamma[5/2 + n] MeijerG[{{}, {2 + n}}, {{-(1/2), 1, 3/2}, {}}, z^2/4])/(Sqrt[π] BesselK[2, z]) *)

This expression requires high precision to evaluate successfully

tab = Table[int1[1][SetPrecision[50, prec]], {prec, 10, 70, 10}] (* {0.*10^35, 0.*10^25, 0.*10^14, 0.*10^4, 0.25795, 0.25794538343534, 0.257945383435342238585179} *) Precision /@ tab (* {0., 0., 0., 0., 4.4595, 13.8895, 23.871} *)

For numeric integration

int2[n_Integer?NonNegative][z_Real?Positive] := (z^2/BesselK[2, z])*NIntegrate[ ((x^2 - 1)^(n + (3/2))/x^(2 n + 1)) Exp[-z*x], {x, 1, Infinity}, WorkingPrecision -> Precision[z]]

int2 requires less precision than int1

tab2 = int2[1] /@ {50., 50.0`10, 50.0`20, 50.0`30} (* {0.257945, 0.25794539, 0.257945383435342239, 0.2579453834353422385851787618} *) Precision /@ tab2 (* {MachinePrecision, 8.26731, 18.2673, 28.2673} *) int1[3][1000.0`900] // N (* 9.1906*10^-7 *) int2[3][1000.0`100] // Quiet // N (* 9.1906*10^-7 *)

EDIT: Approximations for large and small z

For large z

int3[n_Integer?NonNegative, z_?Positive] = Evaluate@ Assuming[Element[n, NonNegativeIntegers], Asymptotic[(2*Gamma[5/2 + n]*MeijerG[{{}, {2 + n}}, {{-(1/2), 1, 3/2}, {}}, z^2/4])/ (Sqrt[Pi]*BesselK[2, z]), {z, Infinity, 3}] // FullSimplify] (* (1/Sqrt[π])2^(-2 + n) z^(-3 - n) (-3 (1 + n) (130 + n (410 + n (402 + n (178 + n (37 + 3 n))))) + 2 (1 + n) (55 + n (109 + n (55 + 9 n))) z - 8 (1 + n) (5 + 3 n) z^2 + 16 z^3) Gamma[5/2 + n] *)

Comparing with int1

Table[ Grid[ Join[ {{StringForm["z = ``", z], SpanFromLeft}, {n, int1, int3}}, Table[ {n, int1[n][SetPrecision[z, 900]], int3[n, z]}, {n, 0, 3}]] /. x_Real :> N[x], Frame -> All], {z, {1000., 200., 100.}}] // Column

enter image description here

For small z

int4[n_Integer?NonNegative, z_?Positive] = Evaluate@ Assuming[Element[n, NonNegativeIntegers] && z > 0, Asymptotic[(2*Gamma[5/2 + n]*MeijerG[{{}, {2 + n}}, {{-(1/2), 1, 3/2}, {}}, z^2/4])/ (Sqrt[Pi]*BesselK[2, z]), {z, 0, 5}] // FullSimplify] (* (Sqrt[π] z^4 Gamma[5/2 + n])/(3 n!) + 1/32 z (32 - 16 (1 + n) z^2 + 2 (-8 + 4 EulerGamma (1 + n)^2 - n (16 + 7 n)) z^4 + z^4 ((3 + 4 n (2 + n)) HarmonicNumber[-(1/2) + n] + 8 n (2 + n) Log[z] + Log[z^8/4])) *)

Comparing with int1

Table[ Grid[ Join[ {{StringForm["z = ``", z], SpanFromLeft}, {n, int1, int4}}, Table[{n, int1[n][z], int4[n, z]}, {n, 0, 3}]], Frame -> All], {z, {0.01, 0.25, 0.5}}] // Column

enter image description here

Improve this answer
$\endgroup$
2
  • 1
    $\begingroup$ Thank you @Bob. Please have you a method to express these symbolic complex functions by simple fitted functions of z? $\endgroup$ Commented Oct 3, 2022 at 13:37
  • $\begingroup$ Thank you so much @BobHanlon. I'm very grateful. $\endgroup$ Commented Oct 10, 2022 at 18:59
7
$\begingroup$

Do you have an idea

You can not do numerical integration because you had z inside the integral which had no numerical value. Adding Assuming[Re[z]>0 does not help NIntegrate. It needs an actual numerical value.

One way is to do symbolic integration then use Table to generate the 4 values you wanted

 anti[n_] = Integrate[((x^2 - 1)^(n + (3/2))/x^(2 n + 1)) Exp[-z x], {x, 1, Infinity}, GenerateConditions -> False]

Mathematica graphics

And now

Table[(z^2/BesselK[2, z])*anti[n], {n, 0, 3}]

Mathematica graphics

Note that Integrate gives condition on n and z which I did not show above. Here it is

Mathematica graphics

So you need to make sure that your n and z you use to evaluate this agree. In the Table command above I used different n because that is what you were using.

Improve this answer
$\endgroup$
1
  • $\begingroup$ Thank you @Nasser. Please how to express these complex functions by simple fitted functions of z? $\endgroup$ Commented Oct 3, 2022 at 13:40

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.