Using @CarlWoll's answer to Terrible accuracy of DawsonF (which Q&A makes one suspect at least part of the problem is with DawsonF[]):
(*https://mathematica.stackexchange.com/a/182691*) dawsonF[x_] := -(I/2) E^-x^2 Sqrt[\[Pi]] + I HermiteH[-1, I x] NIntegrate[dawsonF[Sqrt[t]]^2/t, {t, 0, Infinity}, WorkingPrecision -> 160, MaxRecursion -> 20] // N[#, 80] & (* 0.91596559417721901505460351493238411077414937428167213426649811962176301977625477 *)
Addendum
I had said, "at least part of the problem...", because there was some strange behavior I encountered in exploring the problem. I didn't have time to track it down. But thanks in part to @BobHanlon's observation, I now know a little more and have reported the (mis)behavior to WRI support ([Case: 5208413]).
The problem is that in conditions I do not fully understand, the integrand evaluates to Indeterminate. I think NIntegrate[] tries to work around these points, perhaps as if they were removable singularities. However, when that happens, either the accuracy is greatly diminished, or NIntegrate[] fails with a NIntegrate::inumri error ("evaluated to...Indeterminate...") and returns the input.
Consider a call of the following form:
NIntegrate[DawsonF[Sqrt[t]]^2/t, {t, 0, Infinity}, MinRecursion -> min, MaxRecursion -> max, WorkingPrecision -> wp]
If min == max, then NIntegrate[] will run pretty well: No Indeterminate values will be generated and the error will be as low as possible for that level of recursion. You may get a NIntegrate::ncvb ("failed to converge") message if the error is too high for the precision goal at the given WorkingPrecision.
If min is a high enough recursion level to meet the precision goal, then increasing max has no effect. If min is not a high enough recursion level, then increasing max is expected to lower the error. This is what happens until Indeterminate values of the integrand are generated. This seems to happen when the error dips below 10^-wp or so. The error jumps up to around 10^-9 and seems to increase slightly as max increases, the opposite of what one expects. Eventually, NIntegrate[] fails with a NIntegrate::inumri error as mentioned above.
So the "trick" to using the built-in DawsonF[] in the OP's problem is to guess the right MinRecursion/MaxRecursion level for the desired WorkingPrecision.
Strangely enough, if the integrand is evaluated at the values of t that generated Indeterminate in an NIntegrate[] call, the value is computed correctly. It does not return Indeterminate. That is why I suspect that NIntegrate[] shares the blame.
Code for exploration:
count = 0;(* set less than 6 to Echo Indeterminate values *) obj[t_?NumericQ] := Block[{res}, res = DawsonF[Sqrt[t]]^2/t; If[! NumberQ[res], If[ListQ[foo], foo = {foo, Hold[DawsonF[Sqrt[t]]^2/t] -> res}, foo = {Hold[DawsonF[Sqrt[t]]^2/t] -> res} ]; If[++count <= 6, Echo[t -> res]] ]; res ]; foo = {};(* reset to empty list before NIntegrate[obj[t]...] *) NIntegrate[obj[t], {t, 0, Infinity}, MinRecursion -> 3, MaxRecursion -> 5, WorkingPrecision -> 80] foo // Flatten // Length (* number of Indeterminate values *)
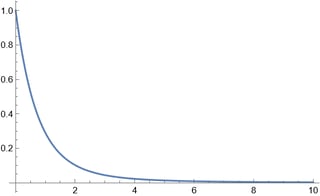 . There is no singularity whatsoever. When $t$ is large, integrand is of order $O(1/t^2)$, so the integral converge.
. There is no singularity whatsoever. When $t$ is large, integrand is of order $O(1/t^2)$, so the integral converge.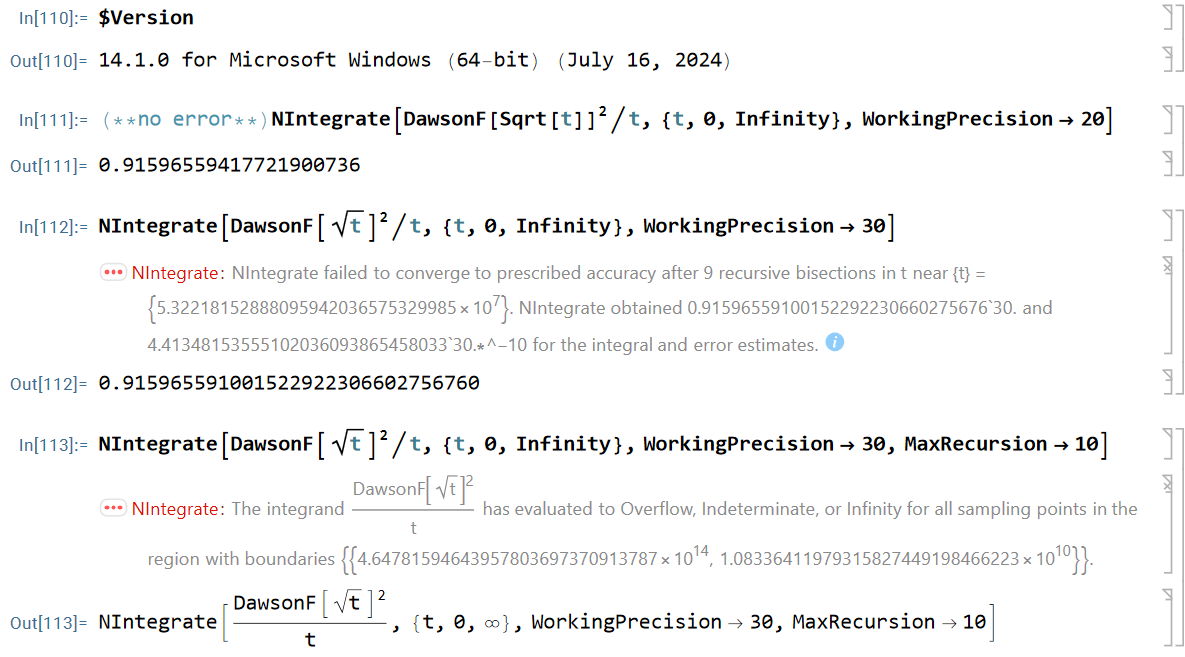
![NIntegrate[DawsonF[Sqrt[t]]^2/t, {t, 0, Infinity}, WorkingPrecision -> 30]](https://i.sstatic.net/iVNiPgRj.png)

N[exact,80]now it gives same result as Maple with no problems. i.sstatic.net/K6nIL7Gy.png0.91596559417721901505460351493238411077414937428167213426649811962176301977625477$\endgroup$DawsonFthatIntegratecannot solve exactly (e.g. replace square by cube, 4th power etc). The above is a toy example to illustrate the problem I encountered when usingNIntegrateon them. $\endgroup$