15
$\begingroup$

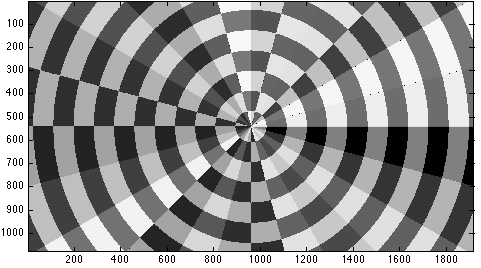
enter image description here

How can I generate such an image and fill every annular sector with a random colour?

Improve this question
$\endgroup$
2
  • 1
    $\begingroup$ ParametricPlot[r {Cos[t], Sin[t]}, {t, 0, 2 Pi}, {r, 0, 5}, MeshShading -> {{Red, Blue}, {Yellow, Green}}] ? $\endgroup$ Commented Feb 25, 2014 at 21:29
  • 1
    $\begingroup$ Related: mathematica.stackexchange.com/questions/10923/… $\endgroup$ Commented May 25, 2015 at 14:21

5 Answers 5

Reset to default
18
$\begingroup$

With V10 came RandomColor and ColorSpace

Using Michael E2's wonderful solution

plot = ParametricPlot[r {Cos[t], Sin[t]}, {r, 0, 12}, {t, 0, 2 Pi}, ImageSize -> 500, Mesh -> 13, MeshShading -> {{Red, Red}, {Red, Red}}, PlotRange -> {{-9, 9}, {-4, 4}}]; Grid @ Partition[Table[plot /. poly_Polygon :> {RandomColor[ColorSpace -> space], poly}, {space, {"RGB", "XYZ", "CMYK", "Grayscale"}}], 2]

enter image description here

Improve this answer
$\endgroup$
2
  • $\begingroup$ eldo, just saw this.. Neat (+1) $\endgroup$ Commented Oct 10, 2014 at 18:55
  • 2
    $\begingroup$ @eldo very nice...thank you for introducing me to RandomColor and ColorSpace :) $\endgroup$ Commented May 24, 2015 at 8:15
19
$\begingroup$

Hmm...Szabolcs beat me to it (in a comment) by one minute...

plot = ParametricPlot[r {Cos[t], Sin[t]}, {r, 0, 12}, {t, 0, 2 Pi}, Mesh -> 23, Axes -> False, MeshShading -> {{Red, Green}, {Blue, Yellow}}, PlotRange -> {{-9, 9}, {-4, 4}}]; plot /. poly_Polygon :> {RGBColor @@ RandomReal[1, 3], poly}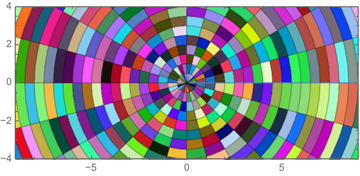

Mathematica graphics

Improve this answer
$\endgroup$
0
15
$\begingroup$

Making the MeshShading setting Dynamic also works without the need for post-processing:

ParametricPlot[r {Cos[t], Sin[t]}, {r, 0, 12}, {t, 0, 2 Pi}, Mesh -> 23, Axes -> False, MeshShading -> Dynamic@{{Hue@RandomReal[], Hue@RandomReal[]}, {Hue@RandomReal[], Hue@RandomReal[]}}, PlotRange -> {{-9, 9}, {-4, 4}}]

enter image description here

The same trick works in combination with V10 RandomColor:

ParametricPlot[r {Cos[t], Sin[t]}, {r, 0, 12}, {t, 0, 2 Pi}, Mesh -> 23, Axes -> False,BaseStyle->Opacity[.75], MeshShading ->Dynamic@ {{RandomColor[], RandomColor[]}, {RandomColor[], RandomColor[]}}, PlotRange -> {{-9, 9}, {-4, 4}}]

enter image description here

ParametricPlot[r {Cos[t], Sin[t]}, {r, 0, 12}, {t, 0, 2 Pi}, Mesh ->{25,25}, Axes -> False, BaseStyle->Opacity[.75], MeshShading ->Dynamic@Evaluate@ Table[RandomColor[],{25},{2}], PlotRange -> {{-9, 9}, {-4, 4}}]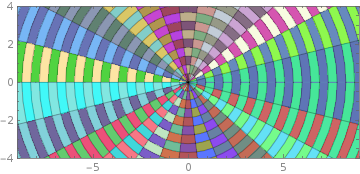

enter image description here

ParametricPlot[r {Cos[t], Sin[t]}, {r, 0, 12}, {t, 0, 2 Pi}, Mesh ->{25,25}, Axes -> False, BaseStyle->Opacity[.75], MeshShading ->Dynamic@Evaluate@ Table[RandomColor[],{2},{25}], PlotRange -> {{-9, 9}, {-4, 4}}]

enter image description here

Improve this answer
$\endgroup$
7
  • 3
    $\begingroup$ Surprising (your use of Dynamic), innovative and upvoteable :) $\endgroup$ Commented Oct 10, 2014 at 18:15
  • $\begingroup$ Could you please explain why this approach works? I'm surprised. +1, of course. $\endgroup$ Commented Oct 10, 2014 at 18:59
  • $\begingroup$ @Alexey, i wish i knew why:) my vague hunch is that the FrontEnd -- as the owner/manager of Dynamic stuff -- triggers new calls to RandomReal/RandomColor since a given call changes something visible ..? Thanks for the vote by the way. $\endgroup$ Commented Oct 10, 2014 at 19:05
  • 1
    $\begingroup$ The InputForm of the output shows that every Polygon has the color specification Dynamic[Hue[RandomReal[]]. It means that the actual reason is inside the Kernel: it keeps the Dynamic head as the head for every color specification it produces from MeshShading. Very interesting and undocumented design decision! Does other plotting functions behave in the same way or only ParametricPlot? A documented way to get the same result is MeshShading->{{Dynamic@Hue@RandomReal[],Dynamic@Hue@RandomReal[]},{Dynamic@Hue@RandomReal[],Dynamic@Hue@RandomReal[]}}. $\endgroup$ Commented Oct 10, 2014 at 19:27
  • 1
    $\begingroup$ We can also get the same result without Dynamic in the output: ParametricPlot[r {Cos[t],Sin[t]},{r,0,12},{t,0,2Pi},Mesh->23,Axes->False,MeshShading->Dynamic@{{Hue@RandomReal[],Hue@RandomReal[]},{Hue@RandomReal[],Hue@RandomReal[]}},PlotRange->{{-9,9},{-4,4}}]/.Dynamic->Identity. $\endgroup$ Commented Oct 10, 2014 at 19:55
11
$\begingroup$

For something somewhat different, I've elected to use BSplineCurve[] + FilledCurve[] to render each annular sector:

sector[{r1_?NumericQ, r2_?NumericQ}, {θ1_?NumericQ, θ2_?NumericQ}] /; r1 < r2 := Module[{cc = Cos[(θ2 - θ1)/2], p1, p2, pm, sk = {0, 0, 0, 1, 1, 1}, sw}, sw = {1, cc, 1}; p1 = Through[{Cos, Sin}[θ1]]; p2 = Through[{Cos, Sin}[θ2]]; pm = Normalize[(p1 + p2)/2]/cc; Prepend[If[r1 == 0, {Line[{{0, 0}}]}, {Line[{r1 p2}], BSplineCurve[r1 {pm, p1}, SplineDegree -> 2, SplineKnots -> sk, SplineWeights -> sw], Line[{r2 p1}]}], BSplineCurve[r2 {p1, pm, p2}, SplineDegree -> 2, SplineKnots -> sk, SplineWeights -> sw]] // FilledCurve]

(I discussed how to use NURBS to make circle arcs in this post.)

Generate the picture:

gr = BlockRandom[SeedRandom[42, Method -> "MersenneTwister"]; (* for reproducibility *) With[{n = 11, θh = π/12, cn = 61 (* color scheme index *)}, Graphics[Table[{ColorData[cn, RandomInteger[{1, ColorData[cn, "Range"][[2]]}]], sector[{r, r + 1}, {θ, θ + θh}]}, {r, 0, n}, {θ, 0, 2 π - θh, θh}], Frame -> True, PlotRange -> {{-9, 9}, {-4, 4}}, PlotRangeClipping -> True]]];

With smooth rendering:

Style[gr, FilledCurveBoxOptions -> {Method -> {"SplinePoints" -> 30}}]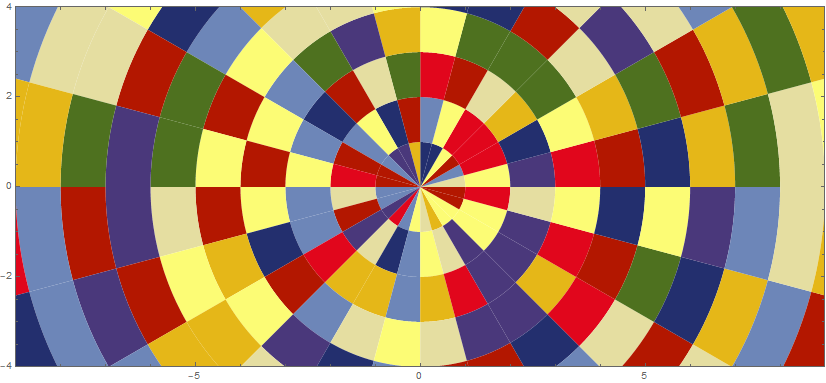

smoothly rendered sectors

You can use version 10's RandomColor[] instead, if you want it.

Improve this answer
$\endgroup$
3
  • 1
    $\begingroup$ Your annular sectors look very polygonal to me... But the colour scheme you picked is very pretty. $\endgroup$ Commented May 24, 2015 at 8:08
  • 1
    $\begingroup$ @Rahul, probably there is an internal setting that will make the B-splines look more circular, but I haven't found it yet... :( $\endgroup$ Commented May 24, 2015 at 8:12
  • 2
    $\begingroup$ @Rahul It was worth the effort to hunt down: (84247) $\endgroup$ Commented May 24, 2015 at 11:07
6
$\begingroup$

An alternative method based on kguler's finding:

ParametricPlot[r {Cos[t], Sin[t]}, {r, 0, 12}, {t, 0, 2 Pi}, Mesh -> 23, Axes -> False, MeshShading -> {{c, c}, {c, c}}, PlotRange -> {{-9, 9}, {-4, 4}}] /. c :> Hue@RandomReal[]

plot

Note that as well as the kguler's answer this is based on undocumented details of the implementation of ParametricPlot and so will not necessarily work in future versions of Mathematica (but it works in v.8.0.4 and 10.0.1).

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.