5
$\begingroup$

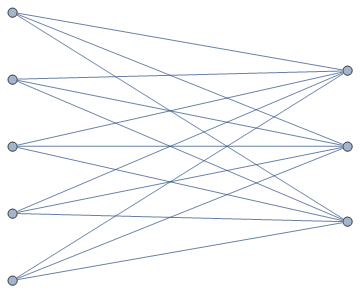
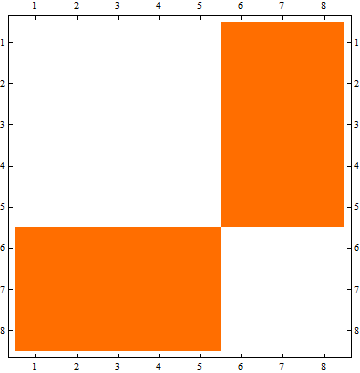
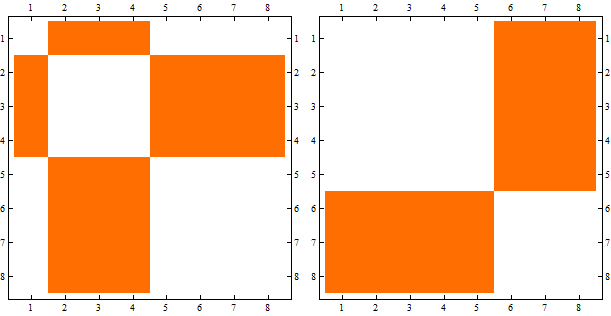
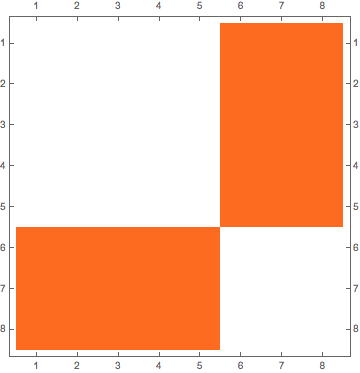
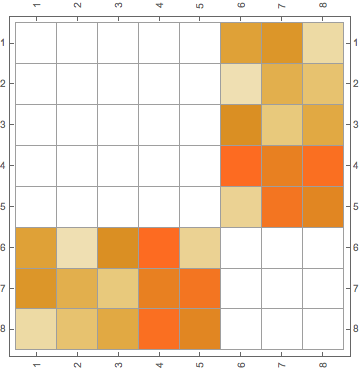
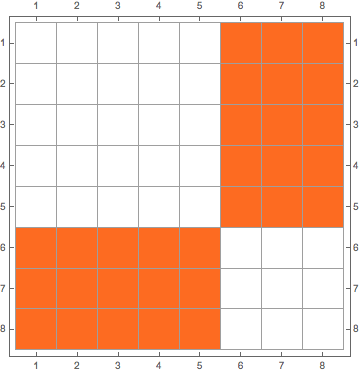
In a bipartite graphs there are two class of nodes, say A and B. Each node of class A may interact only with nodes of the class B, and viceversa. The corresponding adjecency matrix is thus composed by two off-diagonal blocks (if you sort the vertices in an appropriate way).

I realize that when working with adjecency matrix for a given bipartite graphs, sometimes I get the desired order in the adjecency matrix, and thus if I plot it, it is formed by two off-diagonal blocks:

g1=CompleteGraph[{5,3}] m1=AdjacencyMatrix[g1] // MatrixPlot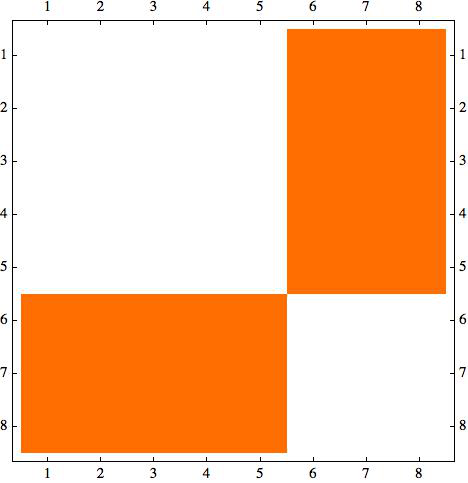

matrix plot of the bipartite graph

However, sometimes if I plot the adjecency matrix directly from the bipartite graphs, now it is not in the desired order:

l2 = CompleteGraph[{5, 3}] // EdgeList; weights = RandomReal[{0.5, 2}, Length[l2]]; g2 = Graph[l2, EdgeWeight -> weights, GraphLayout -> "BipartiteEmbedding"] m2=AdjacencyMatrix[g2] // MatrixPlot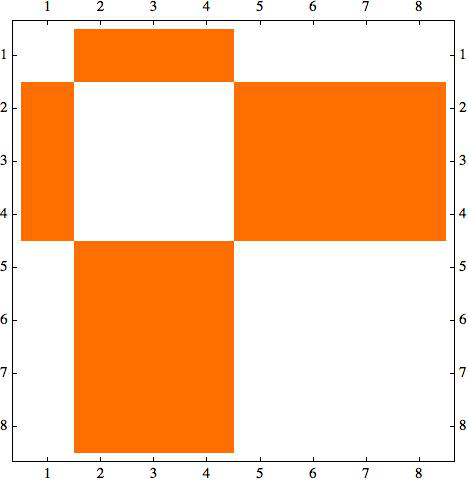

matrix plot of the bipartite graph

I'm trying to find a way to automatically sort m2 so to tranform it in a two off-diagonal blocks matrix.

Improve this question
$\endgroup$
1
  • 1
    $\begingroup$ Note that Dropbox links do not return images, but images embedded in HTML. You need to upload the images to the SE host via the image button above the edit window. $\endgroup$ Commented Apr 19, 2014 at 19:41

3 Answers 3

Reset to default
1
$\begingroup$

From the docs on AdjacencyMatrix:

Rows and columns of the adjacency matrix follow the order given by VertexList

And from the docs on VertexList:

Vertices are taken in the order they appear in the list of edges.

Thus, you have

{VertexList[g1], VertexList[g2]} (* {{1, 2, 3, 4, 5, 6, 7, 8}, {1, 6, 7, 8, 2, 3, 4, 5}} *)

So, you can give an explicit list of vertices as the first argument of Graph to keep the adjacency matrix unchanged:

l2 = CompleteGraph[{5, 3}] // EdgeList; v2 = CompleteGraph[{5, 3}] // VertexList; weights = RandomReal[{0.5, 2}, Length[l2]]; g3 = Graph[v2, l2, EdgeWeight -> weights, GraphLayout -> "BipartiteEmbedding"] m3 = AdjacencyMatrix[g3] // MatrixPlot

enter image description here

enter image description here

Update: Alternatively, you can re-arrange the rows and columns of AdjacencyMatrix[g2] ex post using Ordering as in @Wouter`s answer:

g2 = Graph[l2, EdgeWeight -> weights, GraphLayout -> "BipartiteEmbedding"]; m2 = AdjacencyMatrix[g2]; m2b = m2[[Ordering[VertexList[g2]], Ordering[VertexList[g2]]]]; Row[ MatrixPlot[#, ImageSize -> 300] & /@ {m2, m2b}, Spacer[5]]

enter image description here

Improve this answer
$\endgroup$
4
$\begingroup$

IGraph/M has IGBipartitePartitions for identifying the two partitions.

With your example,

IGBipartitePartitions[g2] (* {{1, 2, 3, 4, 5}, {6, 7, 8}} *)

Reorder the graph vertices:

g3 = IGReorderVertices[Flatten@IGBipartitePartitions[g2], g2]; MatrixPlot@AdjacencyMatrix[g3]

enter image description here

If you just want to visualize the adjacency matrix (with or without weights), but you do not need to compute with it, do both reordering and visualization in one step using IGAdjacencyMatrixPlot.

IGAdjacencyMatrixPlot[g2, Flatten@IGBipartitePartitions[g2]]

enter image description here

This function is quite flexible. Suppose you don't want to show weights and you don't want column labels rotated.

IGAdjacencyMatrixPlot[g2, Flatten@IGBipartitePartitions[g2], EdgeWeight -> None, "RotateColumnLabels" -> False]

enter image description here

The following is a pure-Mathematica implementation of a function that splits a bipartite graph's vertices into two partitions. The idea is that the partition that a vertex belongs to depends on whether its distance from some chosen vertex is odd or even. If the graph is not connected, we need to split each component of the graph into partitions separately, then merge the results together.

singleComponentBipartitePartitions[graph_] := GroupBy[ Transpose@{VertexList[graph], Mod[GraphDistance[graph, First@VertexList[graph]], 2]}, Last -> First ] bipartitePartitions[graph_?BipartiteGraphQ] := Module[{ug}, (* First we convert the graph to undirected and make sure that all edge weights are discarded so that they do not affect the graph distance calculation—should ConnectedGraphComponents start preserving them in a future version. *) ug = Graph[VertexList[graph], EdgeList@UndirectedGraph[graph]]; Values@Merge[ singleComponentBipartitePartitions /@ ConnectedGraphComponents[ug], Catenate ] ] call : bipartitePartitions[expr_] := (Message[bipartitePartitions::inv, HoldForm@OutputForm[call], OutputForm[expr], "bipartite graph"]; $Failed)
Improve this answer
$\endgroup$
14
  • $\begingroup$ You can get the groupings by In[704]:= ConnectedComponents[AdjacencyGraph[1 - AdjacencyMatrix[g2]]] Out[704]= {{1, 5, 6, 7, 8}, {2, 3, 4}}. $\endgroup$ Commented Feb 4, 2018 at 17:15
  • $\begingroup$ @DanielLichtblau That works in this particular case, but it does not work for any bipartite graph. Consider e.g. CycleGraph[6], which is bipartite. AdjacencyGraph[1 - AdjacencyMatrix[g2]] is (almost) the same as GraphComplement[g2]. $\endgroup$ Commented Feb 4, 2018 at 17:25
  • $\begingroup$ Ah. Okay, yes, this will fail in general. $\endgroup$ Commented Feb 4, 2018 at 17:43
  • 1
    $\begingroup$ To be clear: I have no issue with the iGraph/M package*, the motivations for writing it, or use of it in MSE responses. I was commenting on that ornate, but probably very efficient, Mathematica snippet for reordering bipartite graph vertices. (Footnote in next comment) $\endgroup$ Commented Feb 4, 2018 at 22:25
  • 1
    $\begingroup$ I hd missed your question. Yes, the edited version is an improvement for readability. Now upvoted (I guess I forgot to do that several hours ago...) $\endgroup$ Commented Feb 4, 2018 at 23:08
1
$\begingroup$

maybe Map[Part[#,Ordering[First[Normal[m2]]]]&,Normal[m2],{0,1}] ?

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.