tl;dr Don't expect NSolve to give sensible results for equations with no analytic solution.
If you are interested in a "numerical math point of view", use FindRoot or a related function to solve numerically. NSolve tries to find a transformation to an equation it knows exact solutions for, then converts those solutions to machine-precision numbers when returning them.
For example, take the equation x - Sin[x] == 1:
NSolve[x - Sin[x] == 1, x] (* NSolve::nsmet: This system cannot be solved with the methods available to NSolve. >> *) FindRoot[x - Sin[x] == 1, {x, 1}] (* {x -> 1.93456} *)
Your equations look different to NSolve. Note that it first converts approximate to exact numbers (hence the message "solving a corresponding exact system"), so that your troublesome equation is being treated as:
SetPrecision[Power[x + 1.5, x + 1.5] - Power[x, x + 3] == 0, Infinity]
$$ \left(x+\frac{3}{2}\right)^{x+\frac{3}{2}}=x^{x+3} $$
I don't know why NSolve/Solve get hung up on this particular equation, it probably makes a bad guess early on and misses the transformation it used on the other ones.
Just to demonstrate that Mathematica is handling your equations differently, we can look at the output of Solve instead of NSolve:
Solve[Power[x + 1, x + 1] - Power[x, x + 2] == 0, x, Reals]
$$ \text{Root}\left[\left\{(\text{$\#$1}+1) \left(\frac{\text{$\#$1}+1}{\text{$\#$1}}\right)^{\text{$\#$1}}-\text{$\#$1}^2\&,3.141\ldots\right\}\right] $$
Solve[SetPrecision[Power[x + 2.5, x + 2.5] - Power[x, x + 5] == 0, Infinity], x, Reals]
$$ \text{Root}\left[\left\{\frac{25 \sqrt{2 \text{$\#$1}+5} e^{\text{$\#$1} \log \left(\text{$\#$1}+\frac{5}{2}\right)-\text{$\#$1} \log (\text{$\#$1})}}{\text{$\#$1}^5}+\frac{20 \sqrt{2 \text{$\#$1}+5} e^{\text{$\#$1} \log \left(\text{$\#$1}+\frac{5}{2}\right)-\text{$\#$1} \log (\text{$\#$1})}}{\text{$\#$1}^4}+\frac{4 \sqrt{2 \text{$\#$1}+5} e^{\text{$\#$1} \log \left(\text{$\#$1}+\frac{5}{2}\right)-\text{$\#$1} \log (\text{$\#$1})}}{\text{$\#$1}^3}-4 \sqrt{2}\&,3.616\ldots\right\}\right] $$
Very different results...

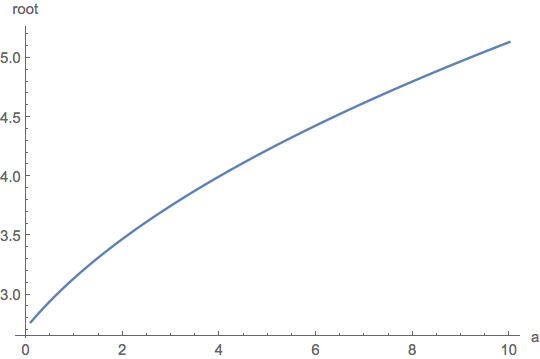
Plot[{Power[x + 1, x + 1] - Power[x, x + 2], Power[x + 1.5, x + 1.5] - Power[x, x + 3]}, {x, 0, 3.5}]and you will see that the curves do not have the same shape. $\endgroup$