Ros control pid gives different input than expected

Question

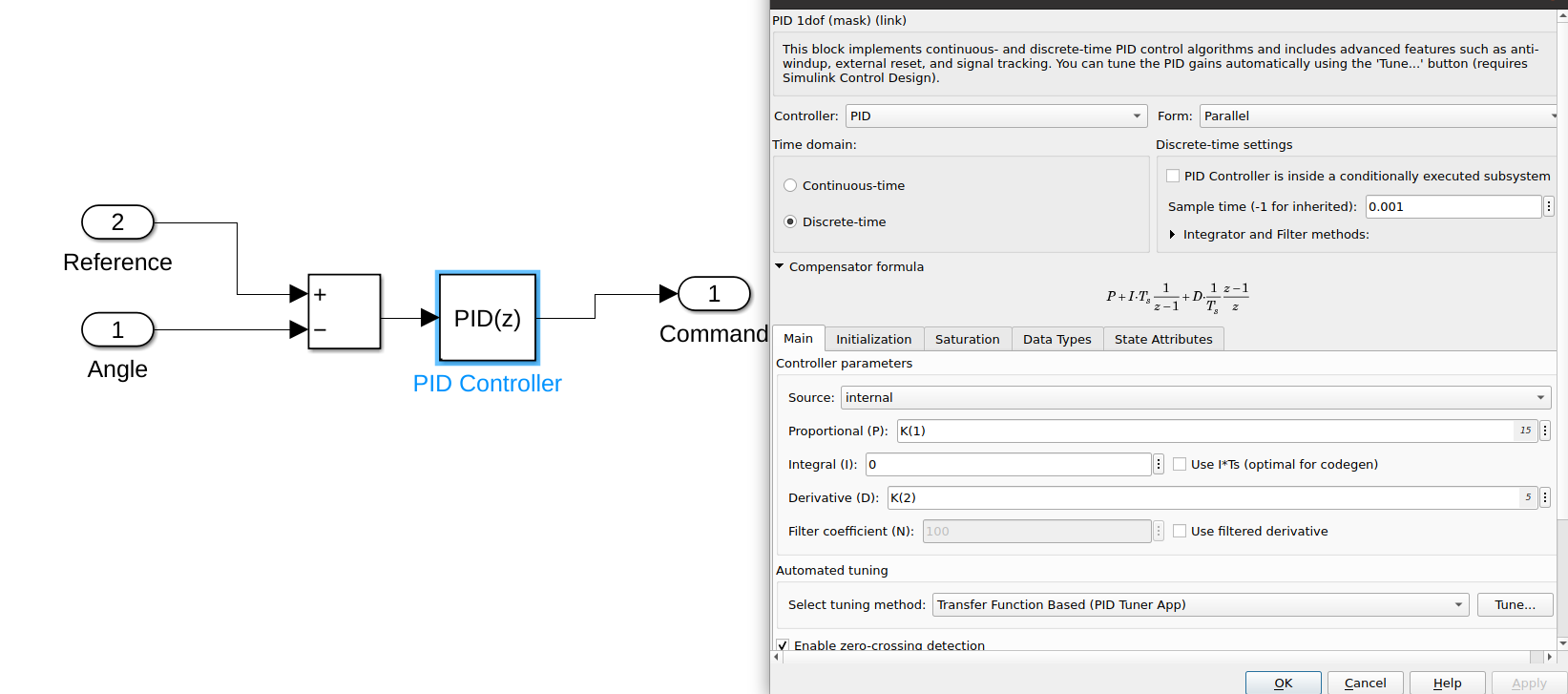
I am trying to match the trajectory i am getting from gazebo simulation using ros_control and matlab for a simple pendulum which rotates in the horizontal plane (so no gravity, no friction and no mechanical reductions).

The Dynamics are governed by the following equation: $$ I\ddot{q} = u $$ where u is the input signal, and $I = 2.4667 \ kgm^2$.

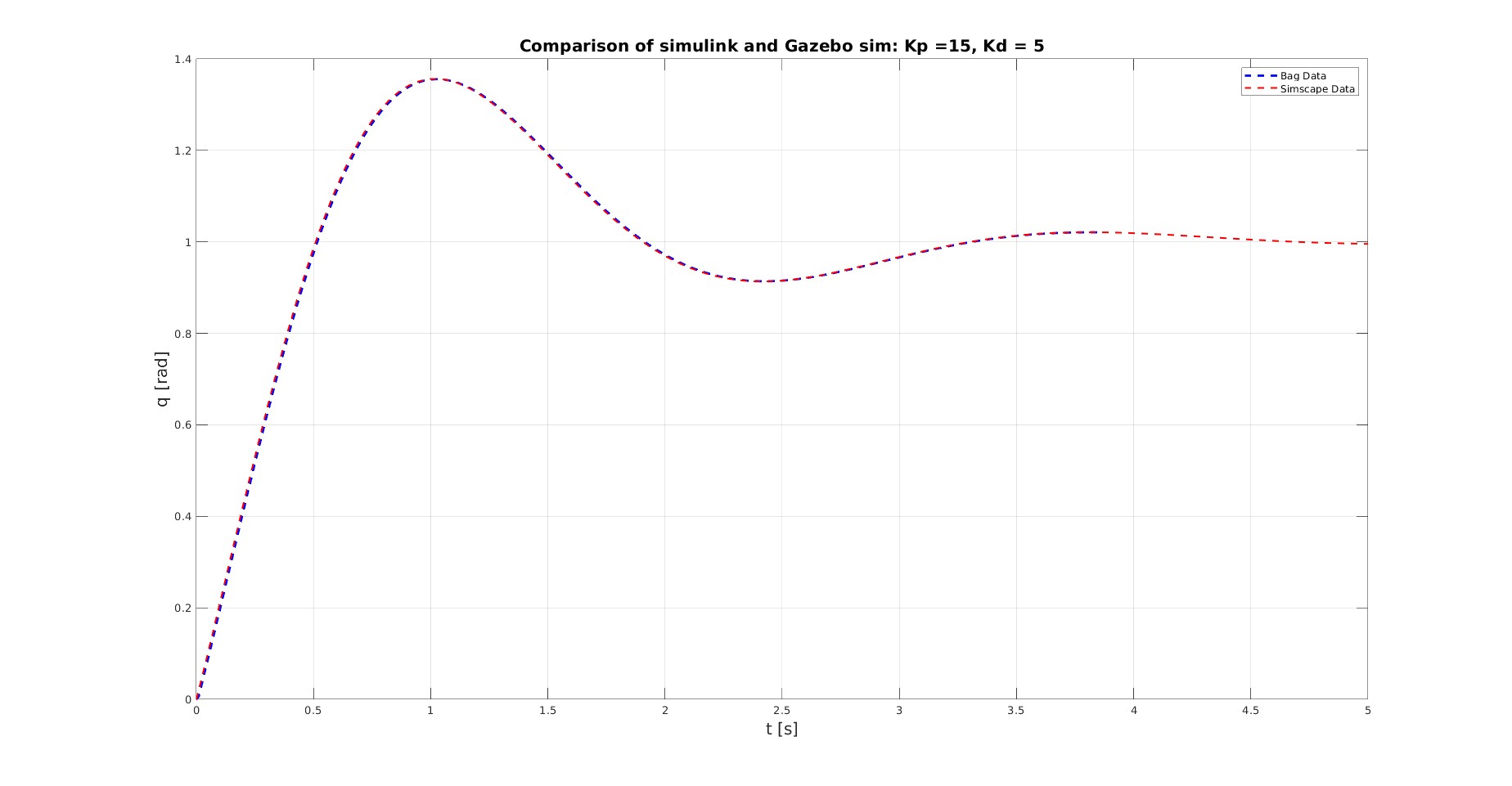
When $u(t) = u(0)$ (step input. I am using the joint_effort_controller in gazebo in this case) the simulations are close enough, as it can be seen from the following graph.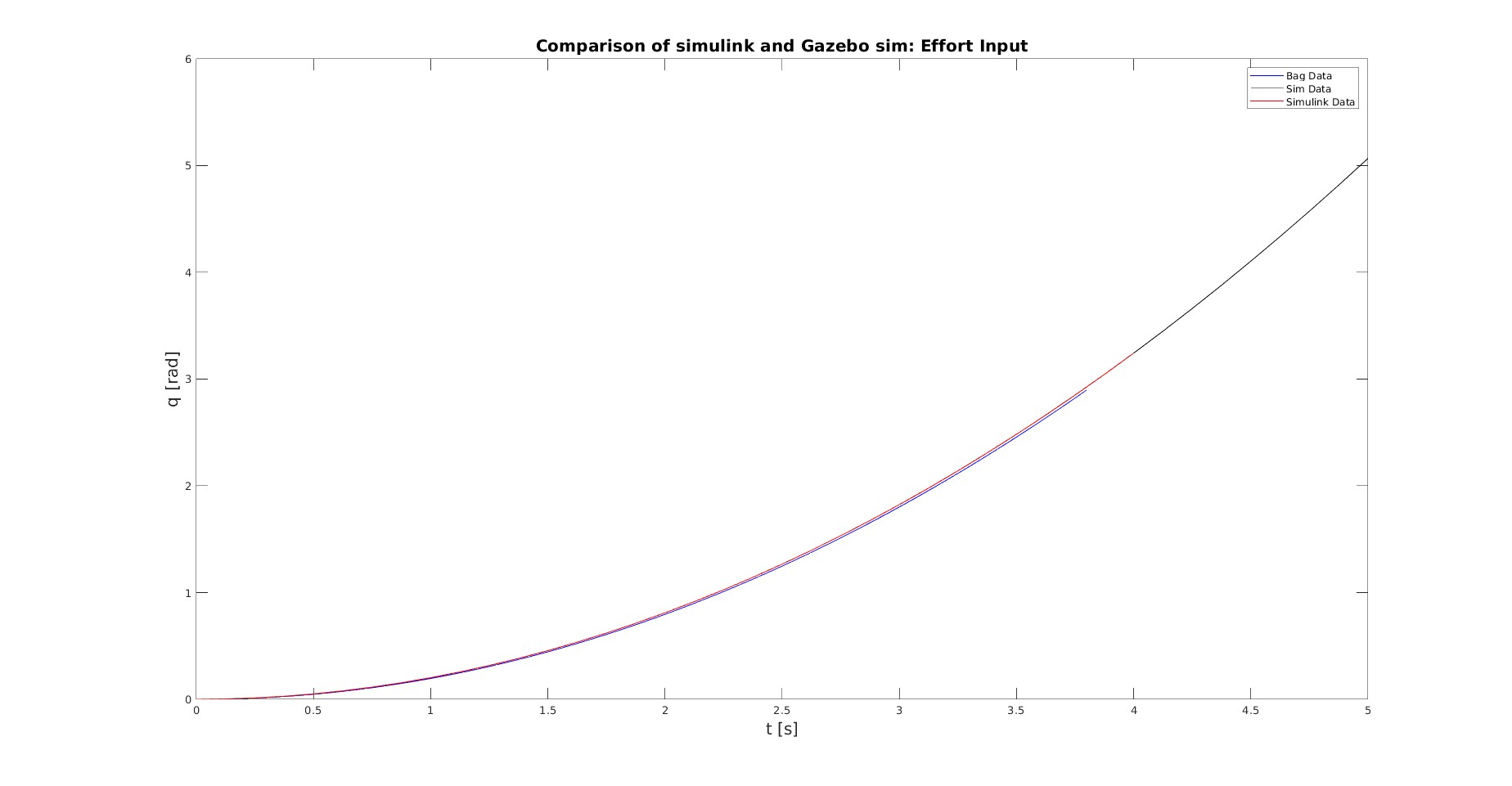

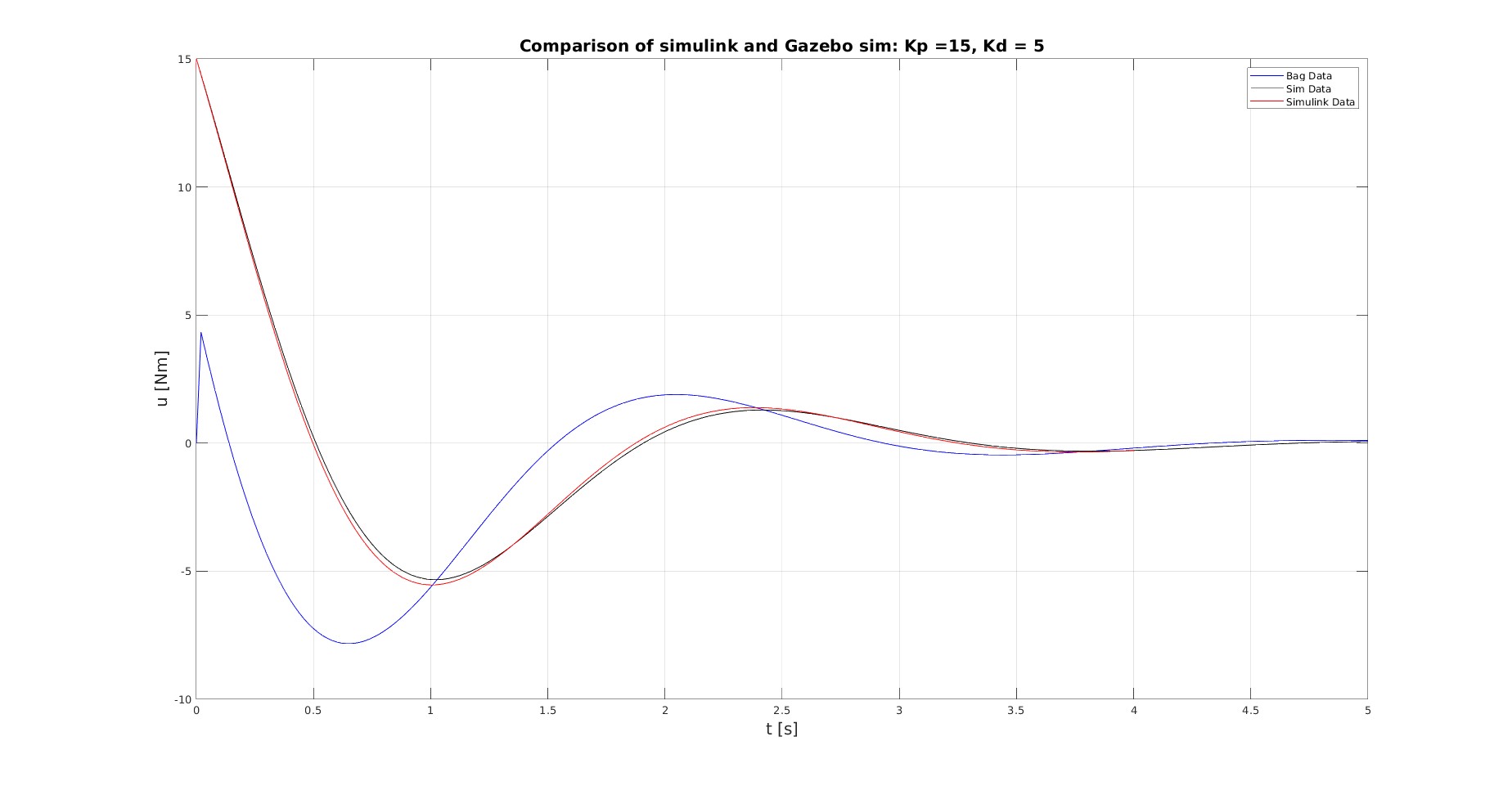
However when i use a pid to control the position (using an effort_controllers/JointPositionController) there are major differences. They can been seen in the following graph: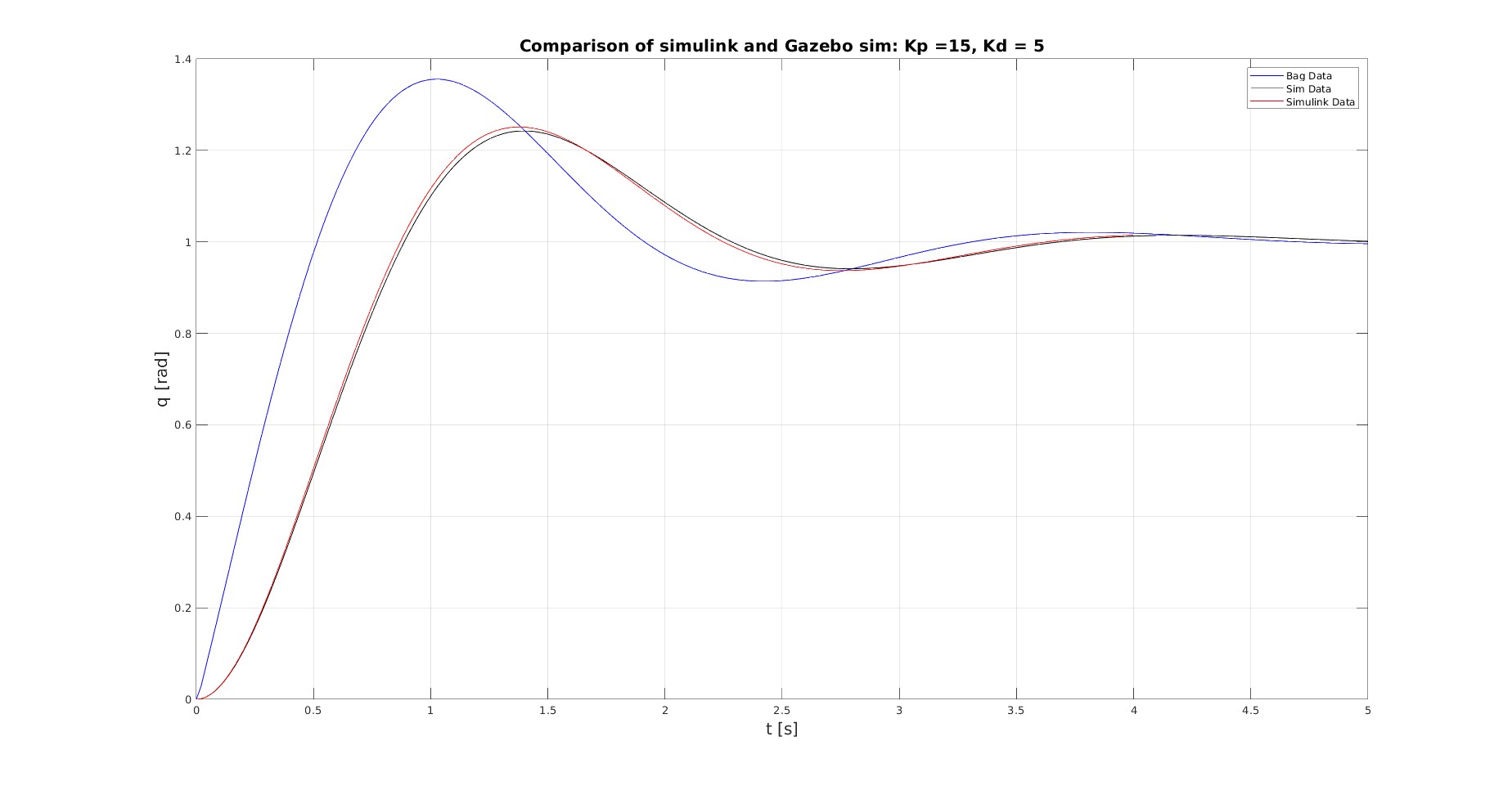

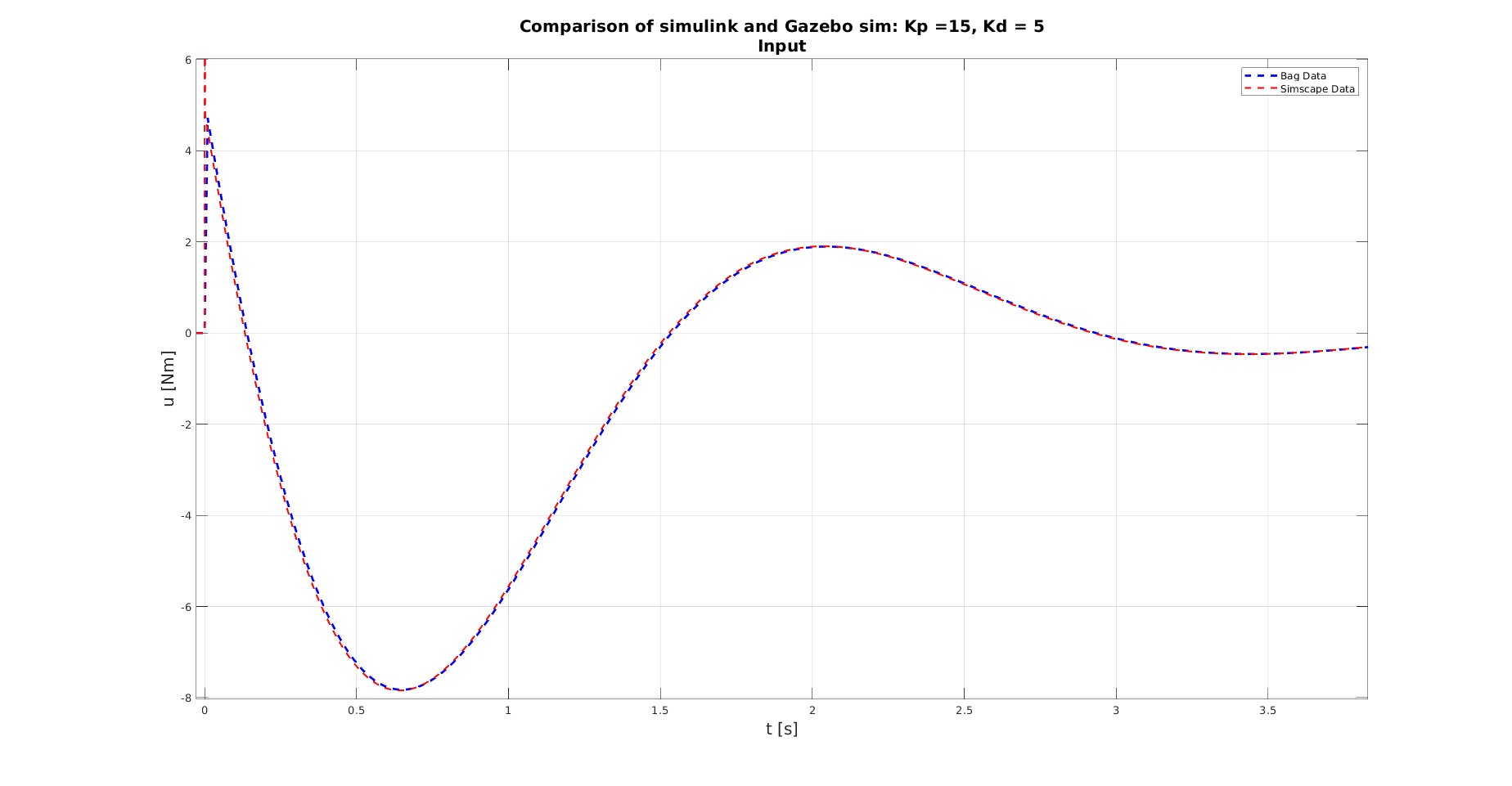
The culprit seems to be the input, as it is considerably different:

The pid gains are chosen as follows:

 pid: {p: 15, i: 0.00, d: 5.0}

In theory, the initial command is ($q_d=1$, and $\{ q_0,\dot{q}_0 \} = \{0,0\}$ ) $$ u_0 = Kp(q_d-q_0) + Kd(0-\dot{q}_0) = 15+0 = 15Nm $$

Matlab gives the expected initial input, however, the commanded torque from ros_control is $u_0 \approx 4 Nm$.

Question I cannot explain how the input command gets that value. And as a result how ros_control calculates the input signal. Any help, hint or idea about what causes this difference will be of great help.

Update Without the derivate term, and only $K_p = 15$ the initial input matches the theoretical one, so $u_0 = 15Nm$. However, from the implementation as it is discussed below:

$$ p_{error} = p_{state}-p_{desired} -> e_{position,0} = -1;$$ $$ d_{error} = (p_{error}-p_{error_last})/T -> e_{velocity,0} = -1/T;$$ I would expect the initial input to be something like that:

$$ u_{ros,0} = -15(-1) -5(-1/T) = 15+5/T$$

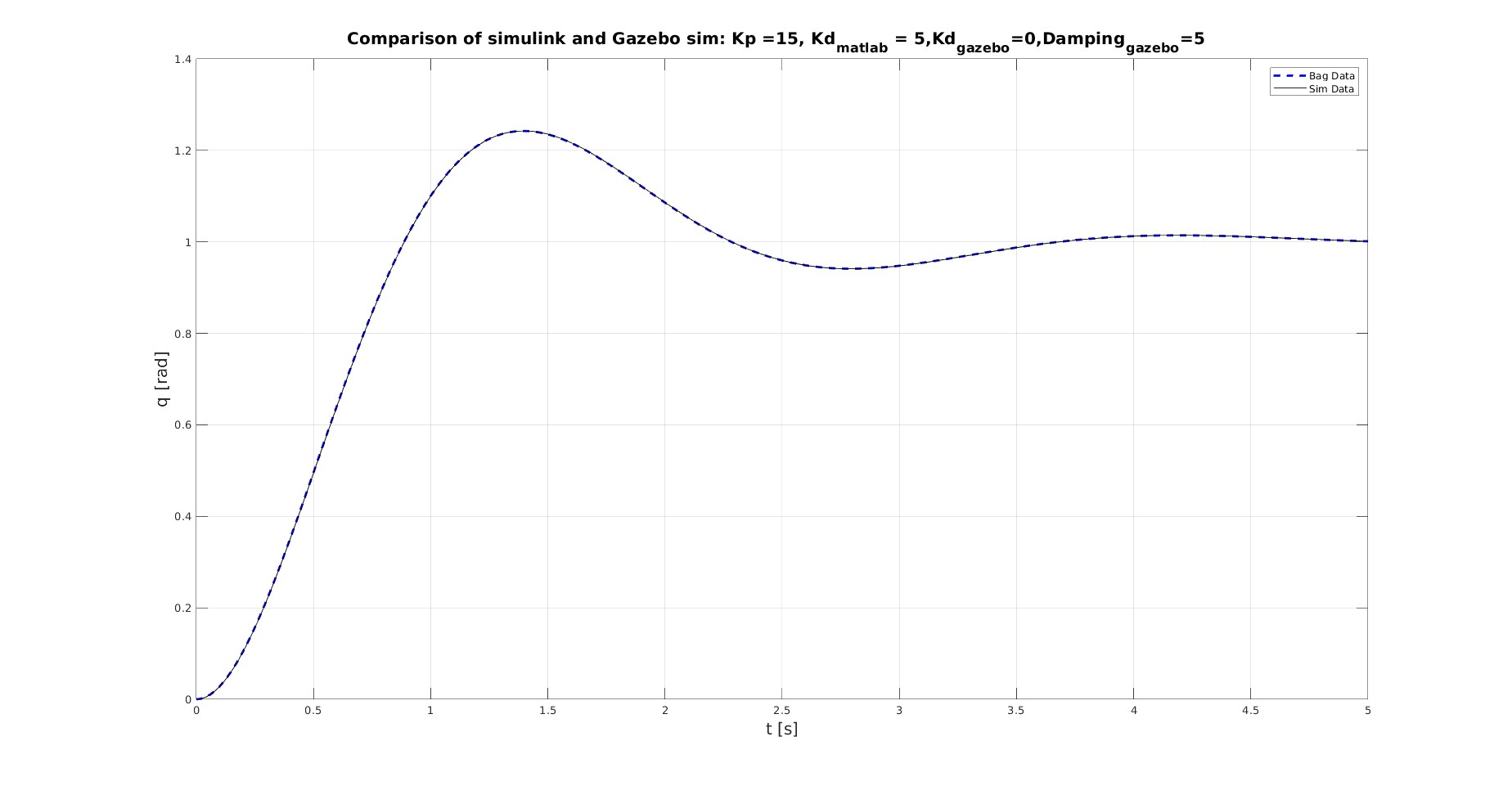
Update 2 If the derivate gain is set to zero, and instead i add damping of 5Ns/rad, then the results between matlab and gazebo match. It can be seen in the next figure.

Extra1 I have to mention that looking the control tooblox API which is used by ros_control for the pid controller, the from of the PID controller is of the following form:

(see lines 331 in the pid.cpp where the function computeCommand is defined. )

Extra2 $$\dot{e}_{position} = \frac{d}{dt}(q_d-q) = -\dot{q} $$

Extra3 The settings for the controller are:

 joint1_position_controller: type: effort_controllers/JointPositionController joint: base_to_link1 pid: {p: 15, i: 0.00, d: 5.0} publish_rate: 50

MIKE PAPADAKIS · Accepted Answer · 2023-03-08 14:06:34Z

There are two wrong things in the initial post:

1st The pid controller publishes its state every 10 calculations. Inside the update command, there is the following code:

// publish state if (loop_count_ % 10 == 0) { if(controller_state_publisher_ && controller_state_publisher_->trylock()) { controller_state_publisher_->msg_.header.stamp = time; ...// rest of the message } } loop_count_++;

So the plot i was getting from the topic controller/state/ doesn't necessarily give me the first command of the system. And from the maths in my question, it can be deduced that i wasn't getting the first command.

Actually, after a while, $|p_{error,i}| < |p_{error,i-1}|$ so $d_{error}>0$ so the $d_{term}$ was positive. Due to the timestep being $Dt=1ms$( something that you can get from the /controller/state/time_step), the $d_{term}$ was also quite large. These reasons resulted in the vastly different input histories of my original post.

2nd Ros control is a discrete digital controller, so the correct way to simulate it is not by using a continuous controller, like: $$ u = K_p e + K_d \dot{e} = K_p (q_d-q) - K_d \dot{q} $$

Using matlab simulink, i used a discrete pid controller (without filtering the derivative) and as expected the simulation results matched.

Also, the imput histories are very simillar (again we can see that i didn't get the initial values from the ros topics):

I also put the controller settings of simulink (K = [15,5]):

Stack Exchange Network

Ros control pid gives different input than expected

1 Answer 1

Hot Network Questions

Ros control pid gives different input than expected

1 Answer 1

Related

Hot Network Questions