A novel approach on gate delay transition based path delay fault model

A NOVEL APPROACH ON GATE DELAY TRANSITION BASED PATH DELAY FAULT MODEL 4 June, 2014 MADHA ENGINEERING COLLEGE By V.Srividhya Reg. No: 211112419007 ME – VLSI Design, Madha Engineering College, Kundrathur. Guided by, Mrs. P. Pattunarajam. M.Tech.,(Ph.D)., Associate Professor ECE Department Madha Engineering College, Kundrathur 1

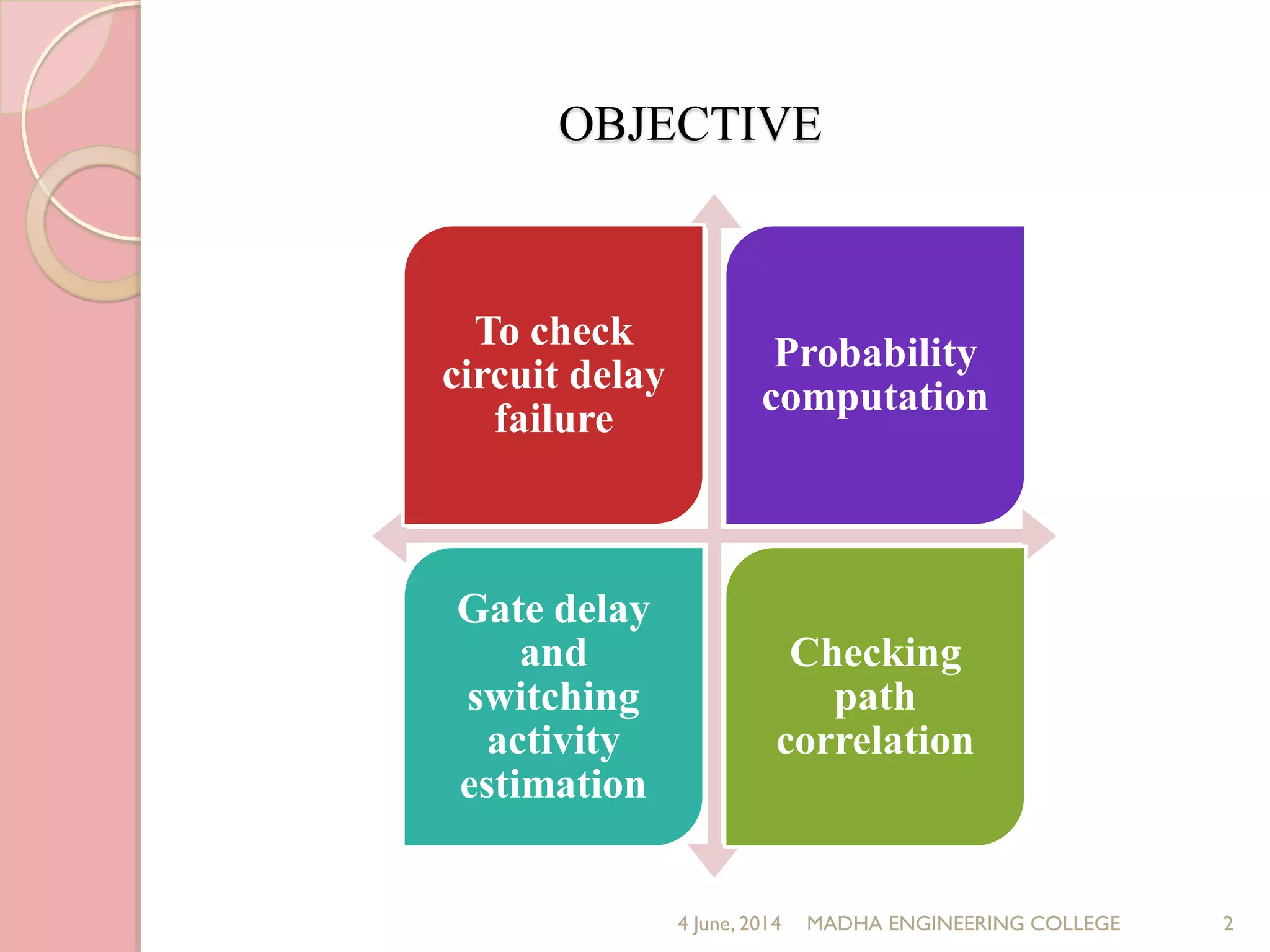
OBJECTIVE 4 June, 2014 MADHA ENGINEERING COLLEGE To check circuit delay failure Probability computation Gate delay and switching activity estimation Checking path correlation 2

INTRODUCTION  Testing consumes more power and time  VLSI suffers from 3-D issue  New path delay model had been done  Path delay faults are identified 4 June, 2014 MADHA ENGINEERING COLLEGE VLSI TECHNOLOGY TIME POWER AREA 3

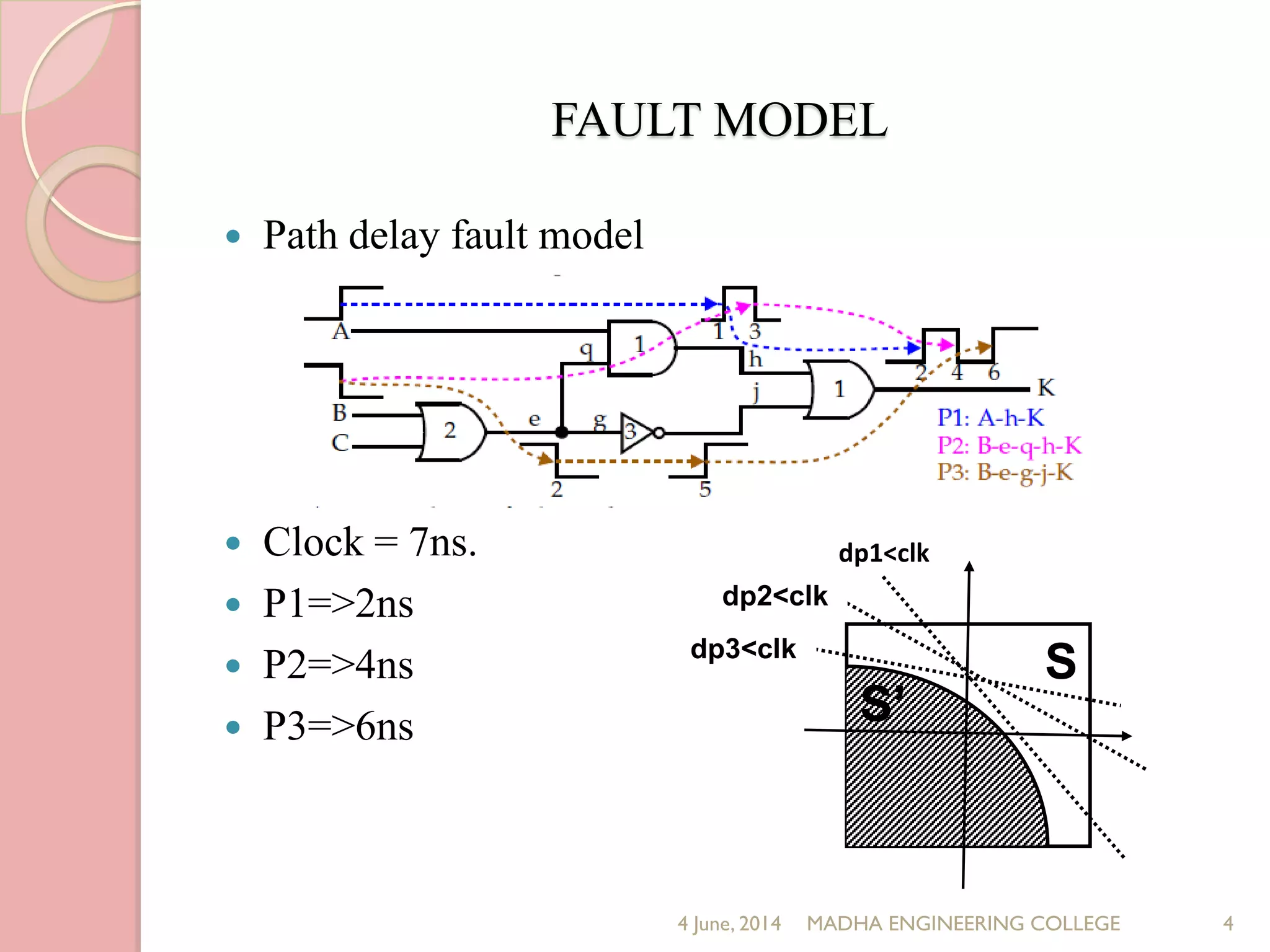
FAULT MODEL 4 June, 2014 MADHA ENGINEERING COLLEGE  Path delay fault model  Clock = 7ns.  P1=>2ns  P2=>4ns  P3=>6ns S S’ dp2<clk dp3<clk dp1<clk 4

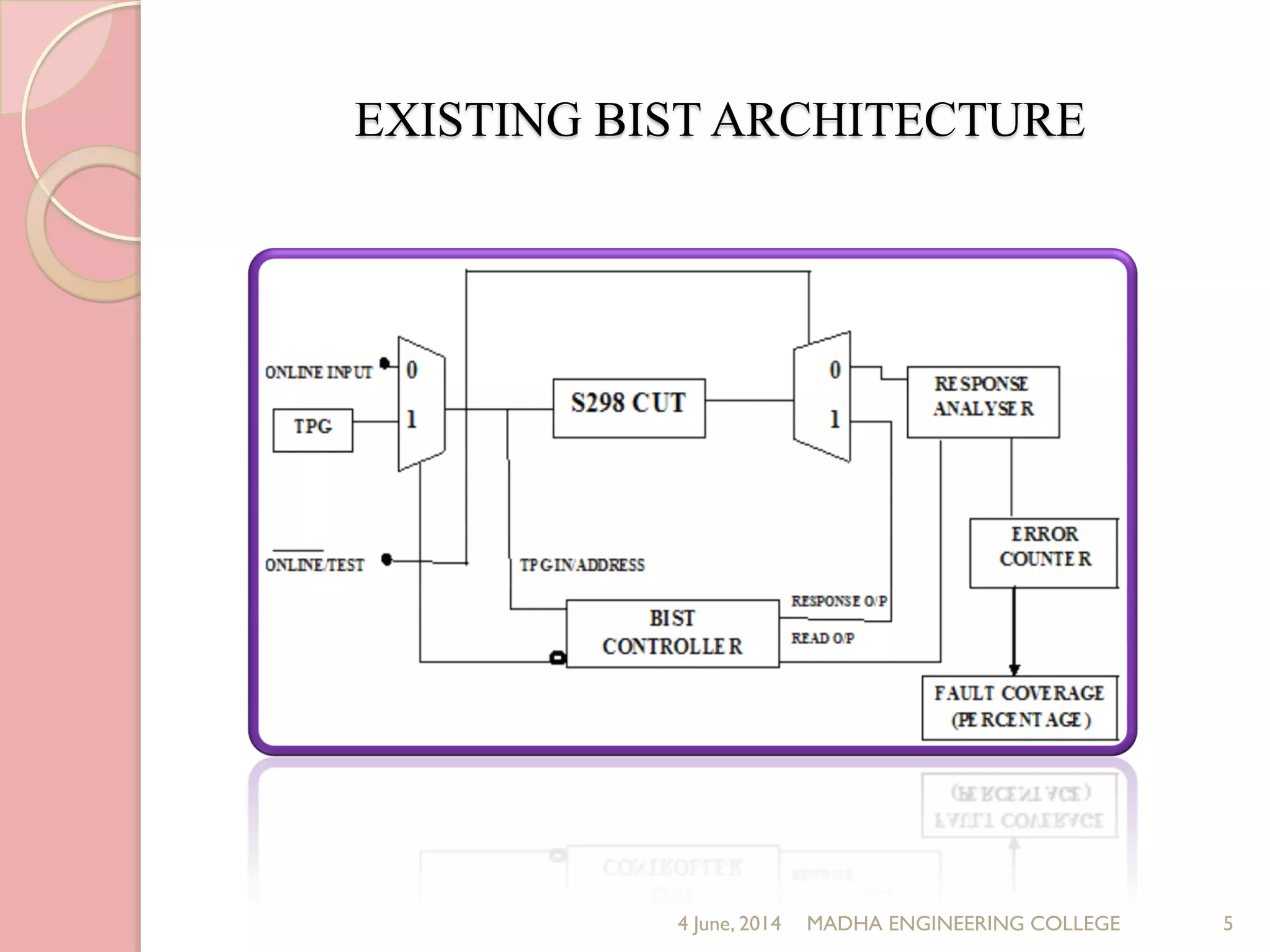
EXISTING BIST ARCHITECTURE 4 June, 2014 MADHA ENGINEERING COLLEGE 5

EXISTING METHOD 4 June, 2014 MADHA ENGINEERING COLLEGE CIRCUIT UNDER TEST TOP LONGEST SEGMENT COVERAGE HEURISTICS UPPER AND LOWER BOUND 6

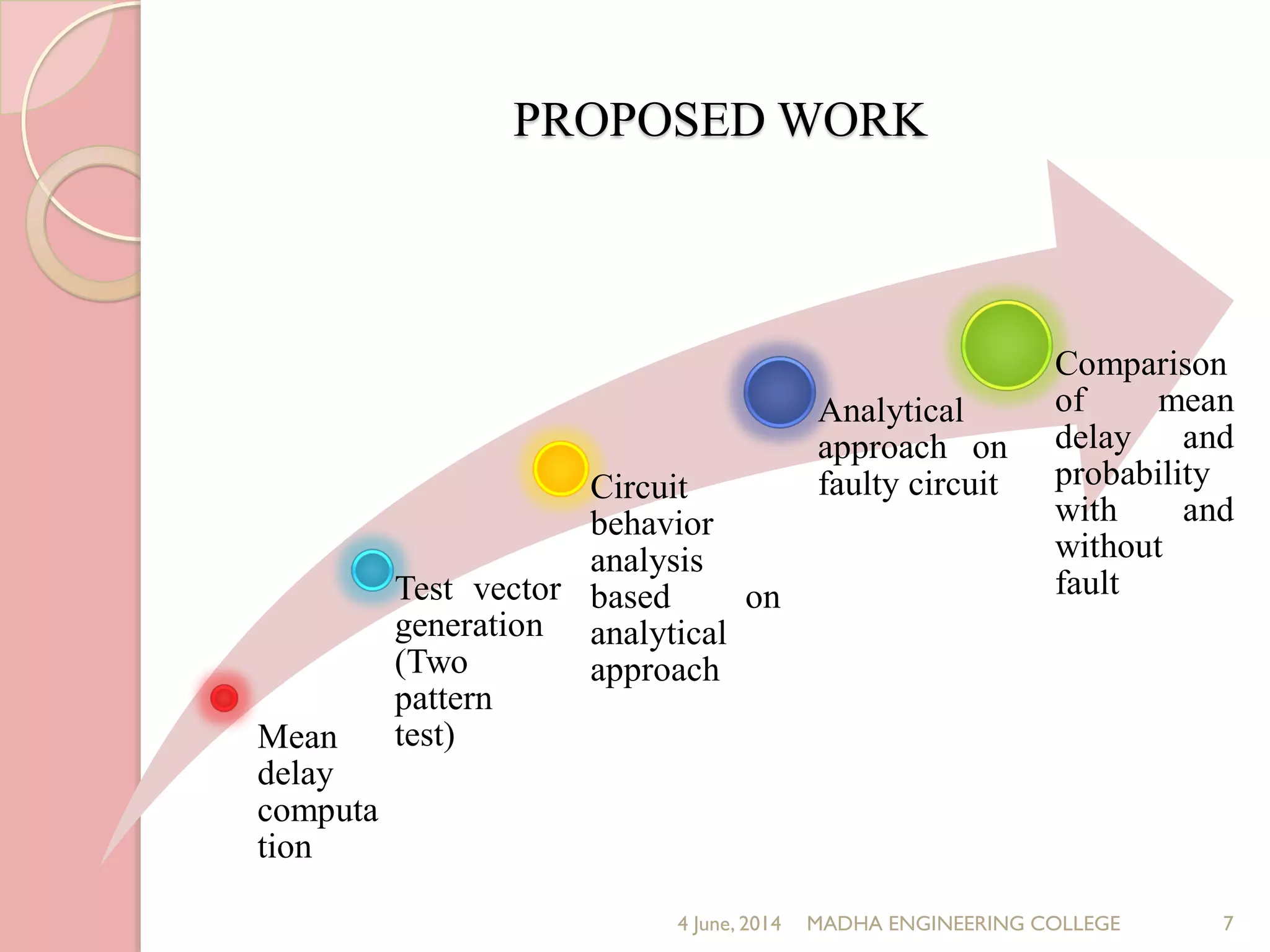
PROPOSED WORK Mean delay computa tion Test vector generation (Two pattern test) Circuit behavior analysis based on analytical approach Analytical approach on faulty circuit Comparison of mean delay and probability with and without fault 4 June, 2014 MADHA ENGINEERING COLLEGE 7

GATE DELAY COMPUTATION 4 June, 2014 MADHA ENGINEERING COLLEGE  Input and output capacitance of each gate in ISCAS’85 c17 benchmark circuit  cin = (cout * gi) / fcap  gi logical effort, fcap product of logical, electrical and branch effort  Gate delay = f + p + q  f = g * h , h = cout/cin  h electrical effort, p parasitic effort, q non-ideal delay 8

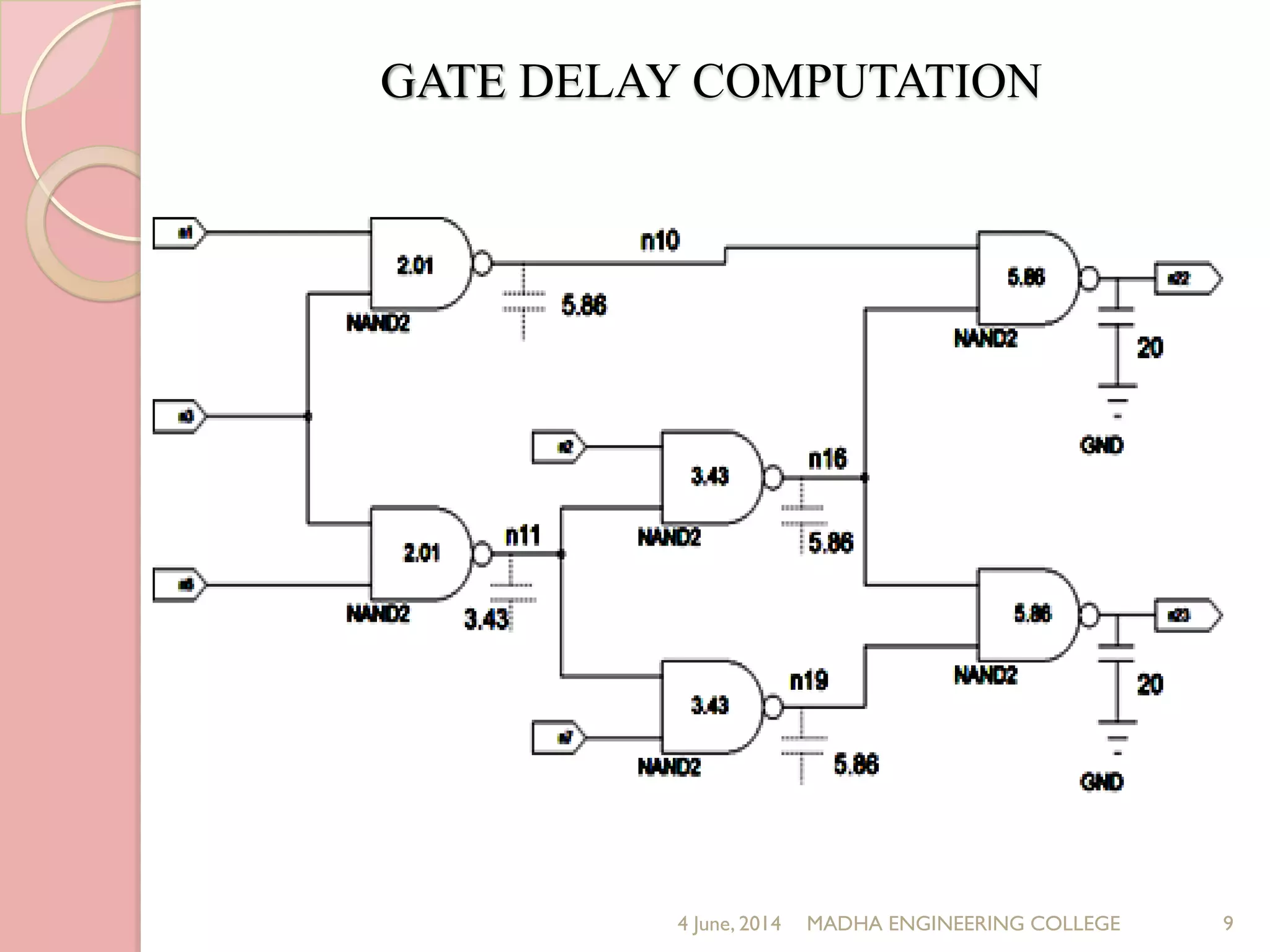
GATE DELAY COMPUTATION 4 June, 2014 MADHA ENGINEERING COLLEGE 9

PATHS IN ISCAS’c17 BENCHMARK CIRCUIT  P1 – n1, n10, n22  P2 – n3, n11, n16, n22  P3 – n6, n11, n16, n23  P4 – n11, n19, n23  P5 – n2, n16, n22  P6 – n2, n16, n23  P7 – n7, n19, n23 4 June, 2014 MADHA ENGINEERING COLLEGE 10

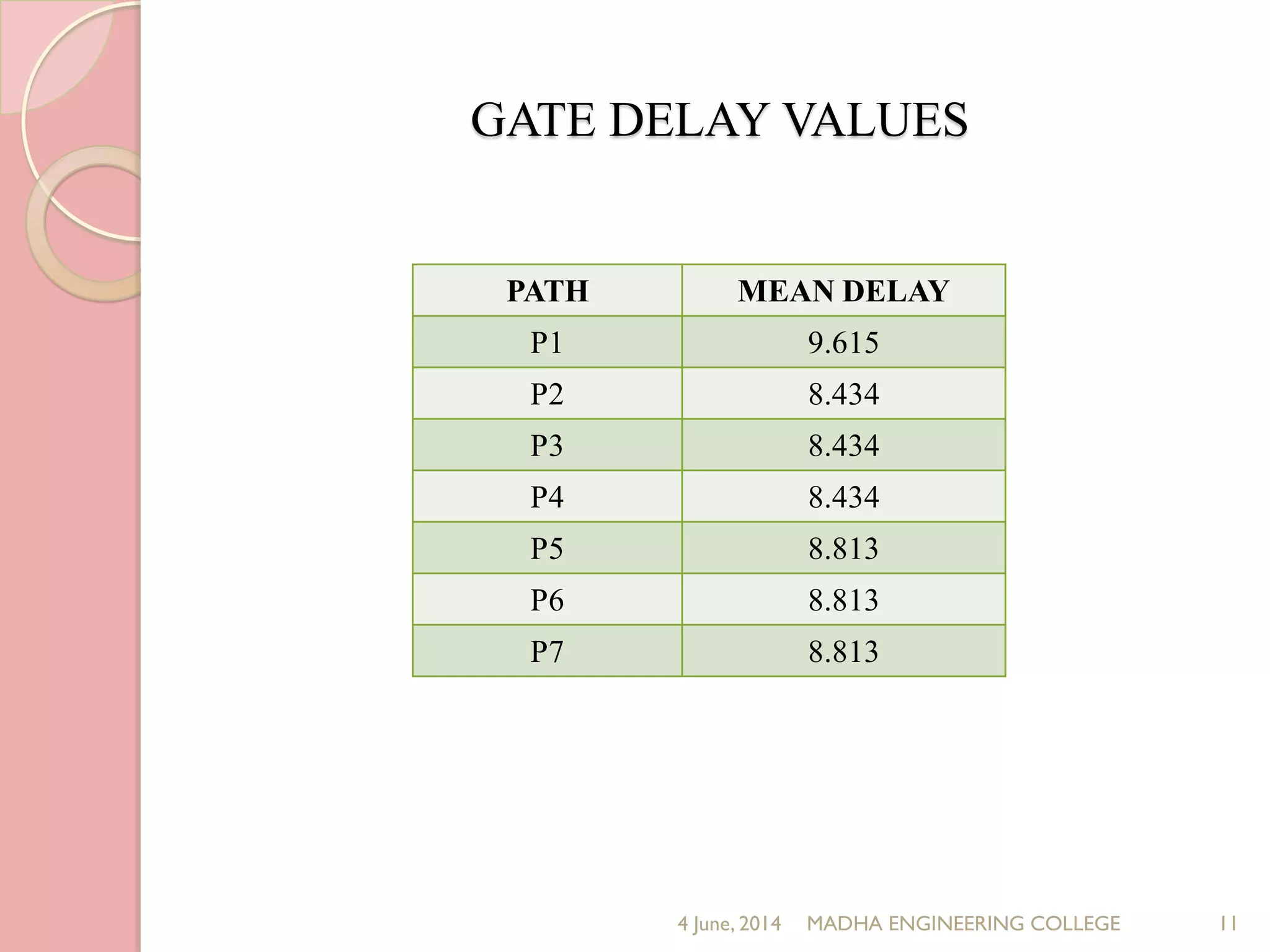
GATE DELAY VALUES 4 June, 2014 MADHA ENGINEERING COLLEGE PATH MEAN DELAY P1 9.615 P2 8.434 P3 8.434 P4 8.434 P5 8.813 P6 8.813 P7 8.813 11

TWO PATTERN INPUT VECTOR GENERATION 4 June, 2014 MADHA ENGINEERING COLLEGE 1 2 3 4 5 0 0 1 1 0 1 2 3 4 5 1 1 1 0 0 CIRCUIT UNDER TEST LFSR LFSR Clock V1 V2 Td 12

GENERATED TWO PATTERN INPUTS 4 June, 2014 MADHA ENGINEERING COLLEGE S.No Initialization pattern Propagation pattern Output1swa n22 Output 2 swa n23 1 11100 00011 1 0 2 11110 10001 1 1 3 11111 11000 2 1 4 01111 10010 4 3 5 00111 11110 5 3 6 10011 11111 6 4 7 11001 01111 8 5 8 01100 00111 9 6 9 10110 10011 9 7 10 01101 11001 10 7 13

SWITCHING ACTIVITY ESTIMATION USING ModelSim Altera 6.5e 4 June, 2014 MADHA ENGINEERING COLLEGE Switching Activity of each net 14

PROBABILITY CALCULATION  Normal distribution is used  Advantage of normal distribution is, it is standard distribution to compute probability of particular area  Mean delay=m  sum of gate delay and switching activity of particular path  Standard deviation=s  Random variable=x  110% of longest path delay  Normal region=(x-m)/s 4 June, 2014 MADHA ENGINEERING COLLEGE 15

PROBABILITY CALCULATION OF TWO PATHS  Normal distribution is used  If two paths are normally distributed, then the following formula applied for joint probability Z=X+Y Mean (Z) = Mean(X) + Mean(Y) Var (Z) = Var(X) + Var(Y) + 2cov(X, Y) The delay of two path is denoted as d2(p1p2) 4 June, 2014 MADHA ENGINEERING COLLEGE 16

PROBABILITY CALCULATION OF THREE PATHS  Max(d2(p1p2)+d2(p1p3)-d1(p1),d2(p1p2)+d2(p2p3)- d1(p2),d2(p1p3)+d2(p2p3)- d1(p3))<=d3(p1p2p3)<=Min(d2(p1p2),d2(p1p3),d2(p2p3))  The max value  upper bound  The min value  lower bound  The average of the upper and lower bound is the probability of three paths. 4 June, 2014 MADHA ENGINEERING COLLEGE 17

PROBABILITY CALCULATION FOR MORE THAN 3 PATHS 4 June, 2014 MADHA ENGINEERING COLLEGE 18

CALCULATION EXAMPLE 4 June, 2014 MADHA ENGINEERING COLLEGE d4(p1p2p3p4) = d3(pLp3p4) d3(pLp3p4) =Max(d2(pLp3)+d2(pLp4)-d1(pL),d2(pLp3)+d2(p3p4)- d1(p3),d2(pLp4)+d2(p3p4)-d1(p4) <= d3(pLp3p4) <= Min(d2(pLp3),d2(pLp4),d2(p3p4)) d1(pL) = d2(p1p2) d2(pLp3) = d3(p1p2p3) d2(pLp4) = d3(p1p2p4) 19

PRACTICAL COMPUTED VALUES  In this proposed work, the computed values for ISCAS’85 c17 benchmark circuit are as follows,  X  Target clock = 110% of 17.9400 = 19.734  X for two paths  2*19.734 = 39.468 4 June, 2014 MADHA ENGINEERING COLLEGE 20

COMPARISON OF FAULTLESS AND FAULTY CIRCUIT 4 June, 2014 MADHA ENGINEERING COLLEGE Faultless Faulty 21

MATHEMATICAL ANALYSIS FROM MATLAB R2010a 4 June, 2014 MADHA ENGINEERING COLLEGE 22

MATHEMATICAL ANALYSIS FROM MATLAB R2010a (Cont….) 4 June, 2014 MADHA ENGINEERING COLLEGE 23

MATHEMATICAL ANALYSIS FROM MATLAB R2010a (Cont….) 4 June, 2014 MADHA ENGINEERING COLLEGE Path index Mean Standard deviation Probability Clock (X) ns P1P2 32.9031 14.4177 0.6756 39.4680 P1P3 31.4031 12.8141 0.7354 P2P3 31.2200 12.7225 0.7416 P1P4 29.6531 11.6957 0.7993 P2P4 29.4700 11.5999 0.8056 P4P5 31.6500 12.7710 0.7451 P5P6 33.8800 14.5263 0.6498 P6P7 29.5466 11.1940 0.8123 P1P6 32.4831 13.5198 0.6973 P1P5 34.4831 15.4774 0.6263 24

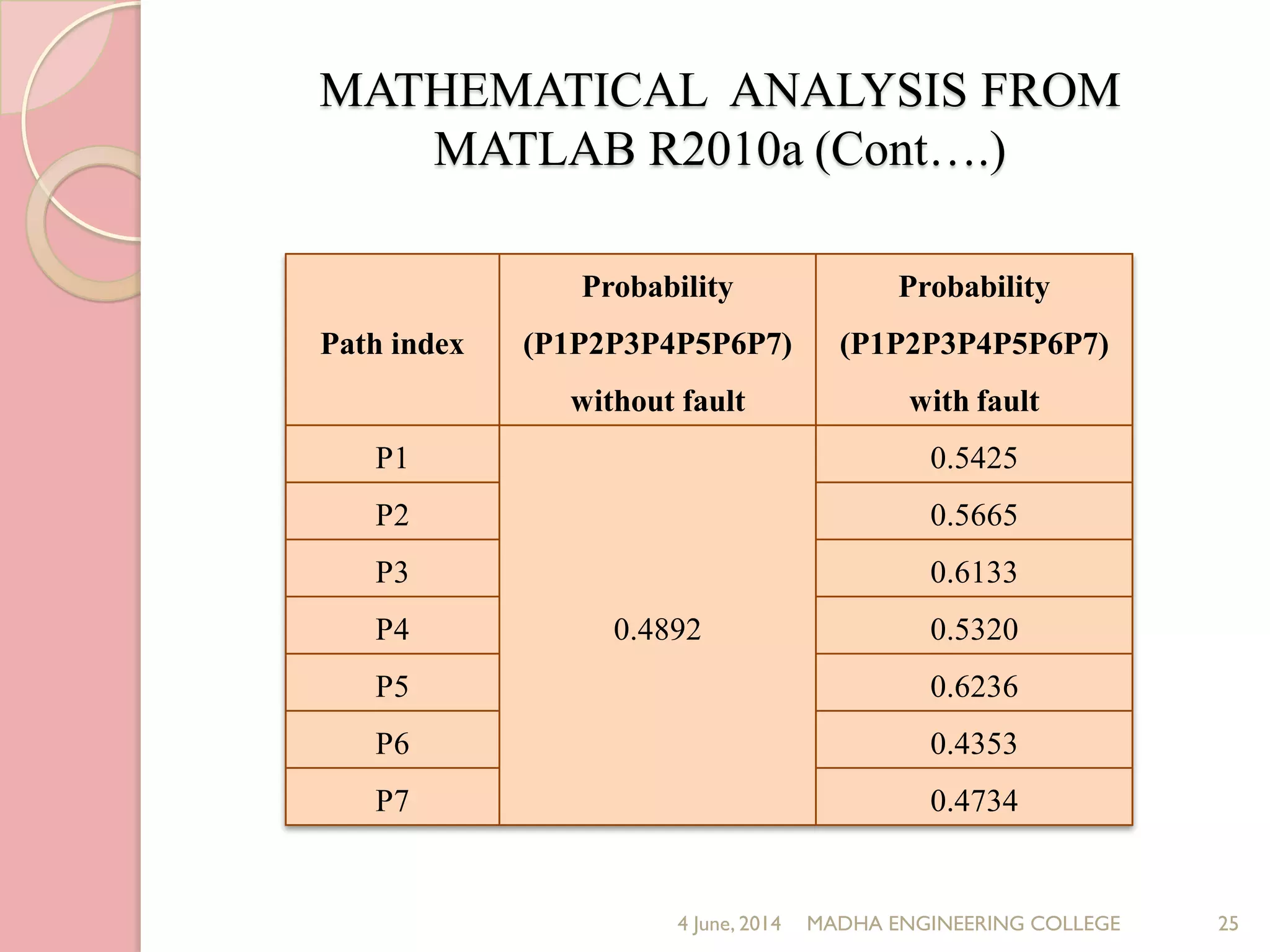
MATHEMATICAL ANALYSIS FROM MATLAB R2010a (Cont….) 4 June, 2014 MADHA ENGINEERING COLLEGE Path index Probability (P1P2P3P4P5P6P7) without fault Probability (P1P2P3P4P5P6P7) with fault P1 0.4892 0.5425 P2 0.5665 P3 0.6133 P4 0.5320 P5 0.6236 P6 0.4353 P7 0.4734 25

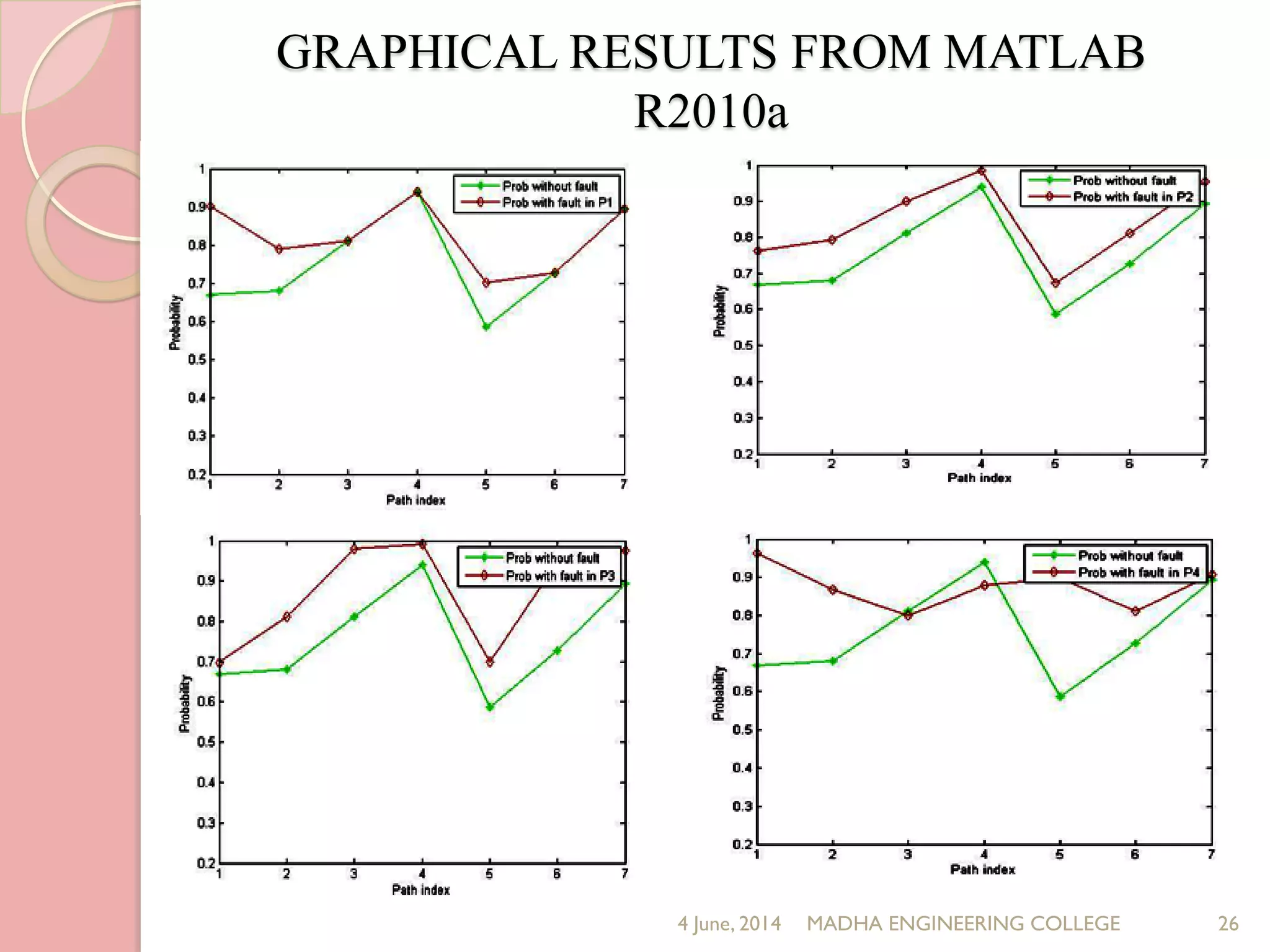
GRAPHICAL RESULTS FROM MATLAB R2010a 4 June, 2014 MADHA ENGINEERING COLLEGE 26

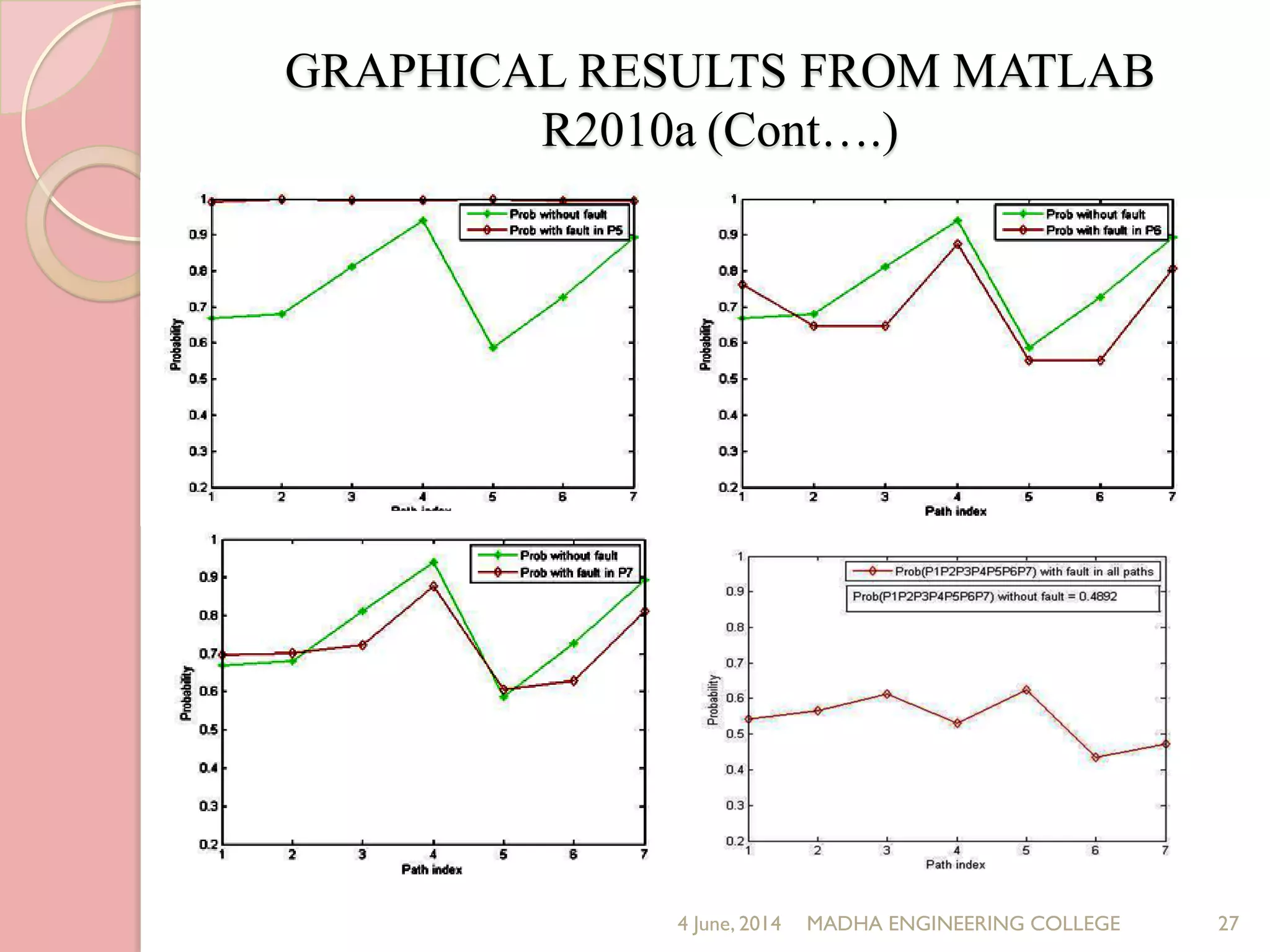
GRAPHICAL RESULTS FROM MATLAB R2010a (Cont….) 4 June, 2014 MADHA ENGINEERING COLLEGE 27

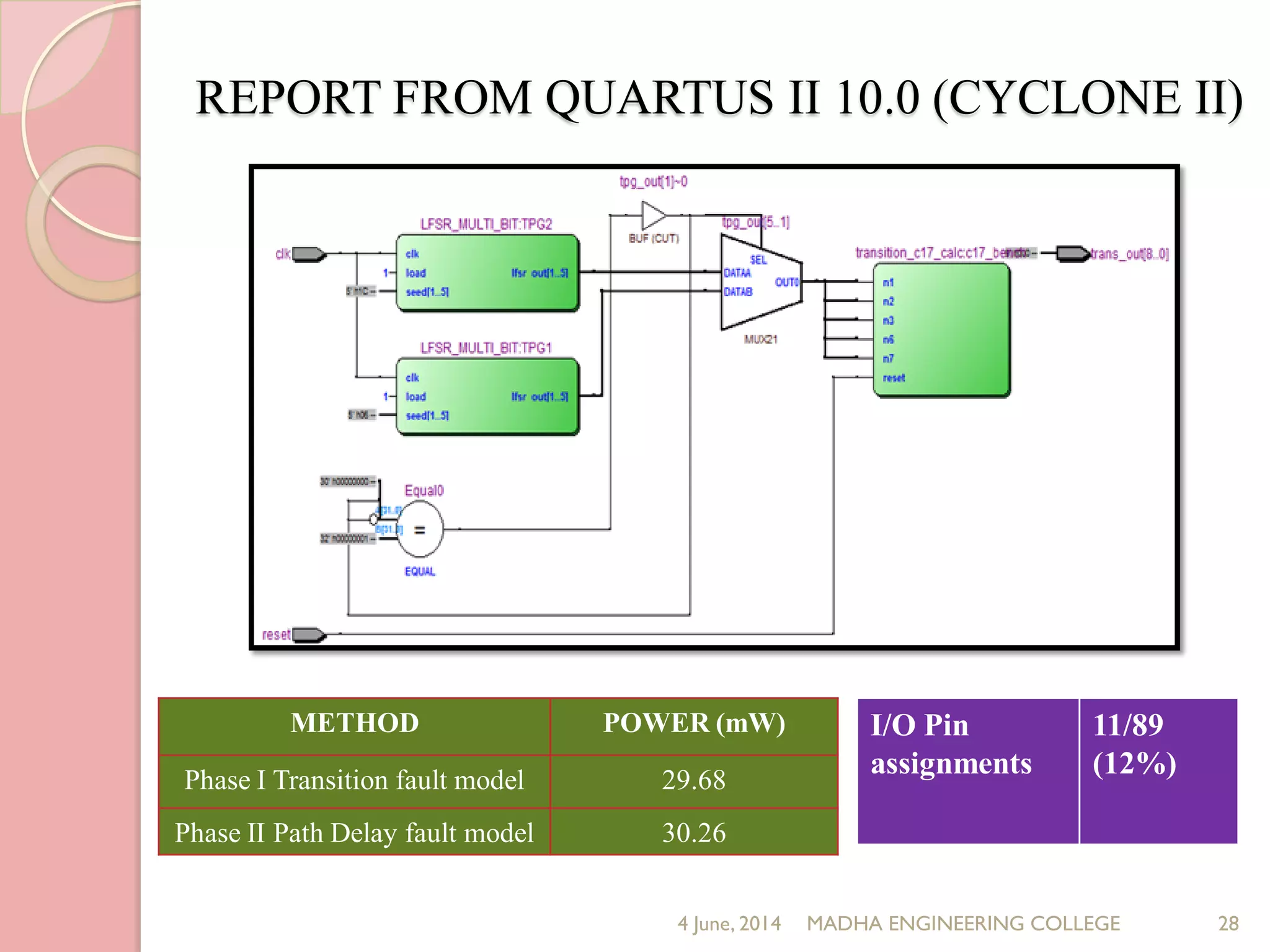
REPORT FROM QUARTUS II 10.0 (CYCLONE II) METHOD POWER (mW) Phase I Transition fault model 29.68 Phase II Path Delay fault model 30.26 4 June, 2014 MADHA ENGINEERING COLLEGE I/O Pin assignments 11/89 (12%) 28

OVERALL RESULTS FROM ALL TOOLS Benchmark Name Power (mW) CPU Time (seconds) I/O Pin required Target Clock(Units) Target Clock for 2 paths(Units) ISCAS’85 c17 30.26 1.1663 11/89(12%) 19.734 39.4680 4 June, 2014 MADHA ENGINEERING COLLEGE 29

CONCLUSION  The probability value depends on the switching activity of the circuit  The circuit switching activity in turn depends on the input vectors.  If the probability is high, the path delay will not exceed the maximum delay  If the probability is low, the path delay will exceed the maximum delay. 4 June, 2014 MADHA ENGINEERING COLLEGE 30

FUTURE WORK 4 June, 2014 MADHA ENGINEERING COLLEGE  In future work, interconnect delay also considered with gate delay, switching activity of the nets with primary input vectors so as to achieve accurate path delay for small and large circuits. 31

REFERENCES [1] Alok S. Doshi and Anand S(2008), “Test Pattern Generator for Built-in Self Test using Spectral Methods ” , Mudlapur Auburn University Dept. of Electrical and Computer Engineering, Auburn, AL, USA doshias. [2] Hongliang Chang and Sachin S. Sapatnekar(2003), “Statistical Timing Analysis Under Spatial Correlations,” Fellow, IEEE.”Computer Aided Design of integrated circuits and systems, IEEE Transactions on vol 24, no. 9. [3] lrith Pomeranz and Sudhakar M. Reddy(Jan.1996), “On the number of tests to delect all path delay faults in combinational logic circuits, “IEEE transactions on computers, vol. 45, No. 1. [4] Jing-Jia Liou, Angela Krstic, Li-C. Wang and Kwang-Ting Cheng(Jun 2002), “False-Path-Aware Statistical Timing Analysis and Efficient Path Selection for Delay Testing and Timing Validation,” Electrical and Computer Engineering Department,University of California, Santa Barbara., IEEE 39th proceedings. [5] Li-C. Wang, Jing-Jia Liou and Kwang-Ting Cheng(Nov 2004), “Critical Path Selection for Delay Fault Testing Based Upon a Statistical Timing Model,” IEEE transactions on computer-aided design of integrated circuits and systems, vol. 23, no. 11,. [6] Vladimir Zolotov, Jinjun Xiong, Hanif Fatemi,and Chandu Visweswariah(May 2010), “Statistical Path Selection for At- Speed Test,” IEEE transactions on computer-aided design of integrated circuits and systems, vol. 29, no. 5. [7] W.B.Jone, W.S.Yeh and S.R.Das(2000),”An Adaptive Path Selection Method for Delay Testing”, IEEE transactions on very large scale integration system, volume 50, issue 5. [8] Wing Ning Li, Sudhakar M. Reddy, Sartaj Sahni(Aug 2002), “On Path Selection In Combinational Logic Circuits,” IEEE transactions in computer aided design of integrated circuits and systems, vol 8, no. 1. [9] Wangqi Qiu D. M. H. Walker, “An Efficient Algorithm for Finding the K Longest Testable Paths Through Each Gate in a Combinational Circuit,” Department of Computer ScienceTexas A&M University, IEEE proceedings, volume 1. [10] Xiang Lu, Zhuo Li, Wangqi Qiu, D. M. H. Walker and Weiping Shi, “Longest Path Selection for Delay Test under Process Variation,” Texas A&M University, College Station, Texas 77843, IEEE transactions on vol 24, no. 12. [11] Zijian He, Tao Lv, Huawei Li and Xiaowei Li(Jul 2013), “Test Path Selection for Capturing Delay Failures Under Statistical Timing Model”IEEE transactions on very large scale integration (VLSI) systems, vol. 21, No. 7. 4 June, 2014 MADHA ENGINEERING COLLEGE 32

4 June, 2014 MADHA ENGINEERING COLLEGE 33

A novel approach on gate delay transition based path delay fault model

More Related Content

Similar to A novel approach on gate delay transition based path delay fault model

Recently uploaded

A novel approach on gate delay transition based path delay fault model