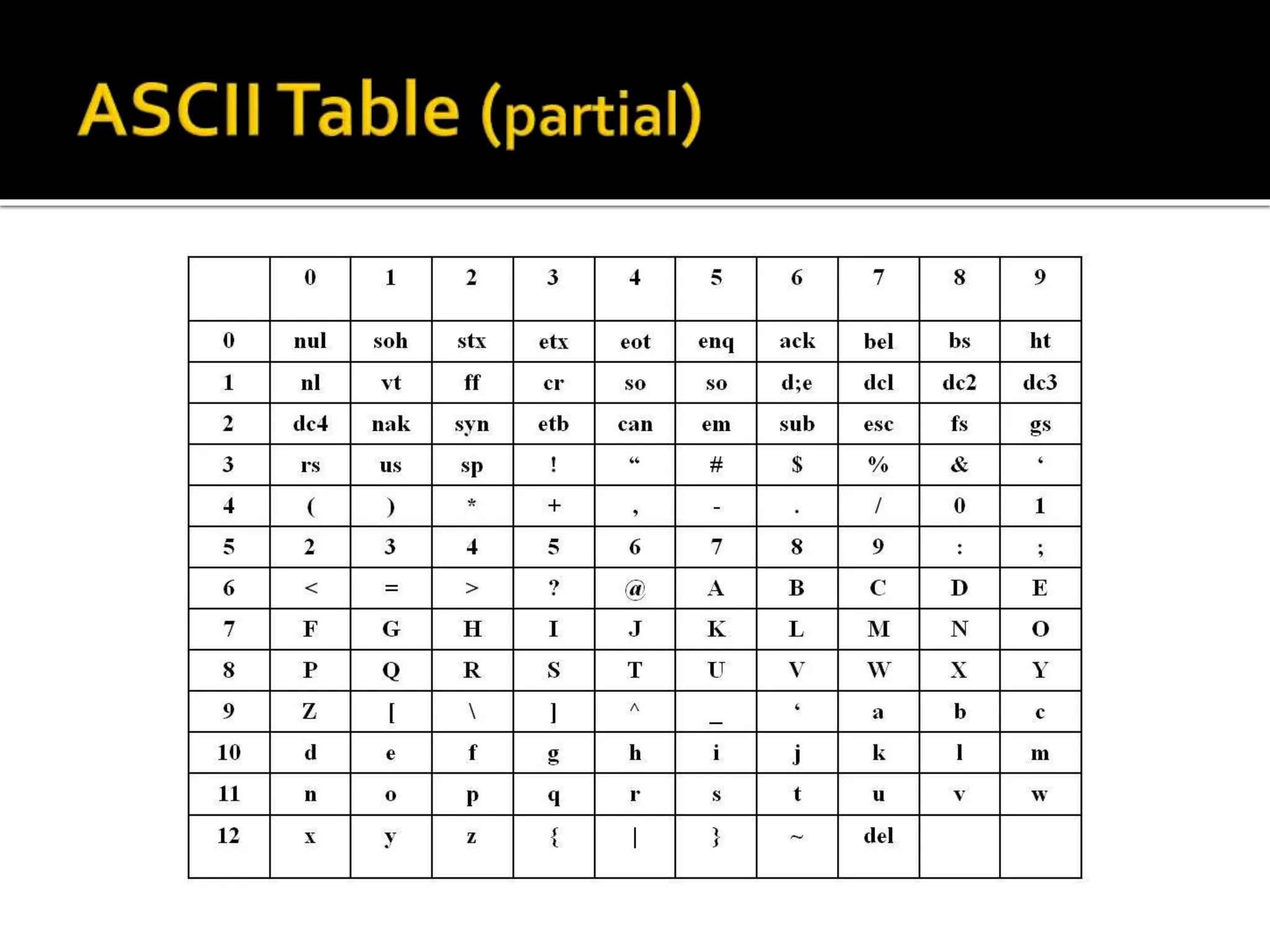
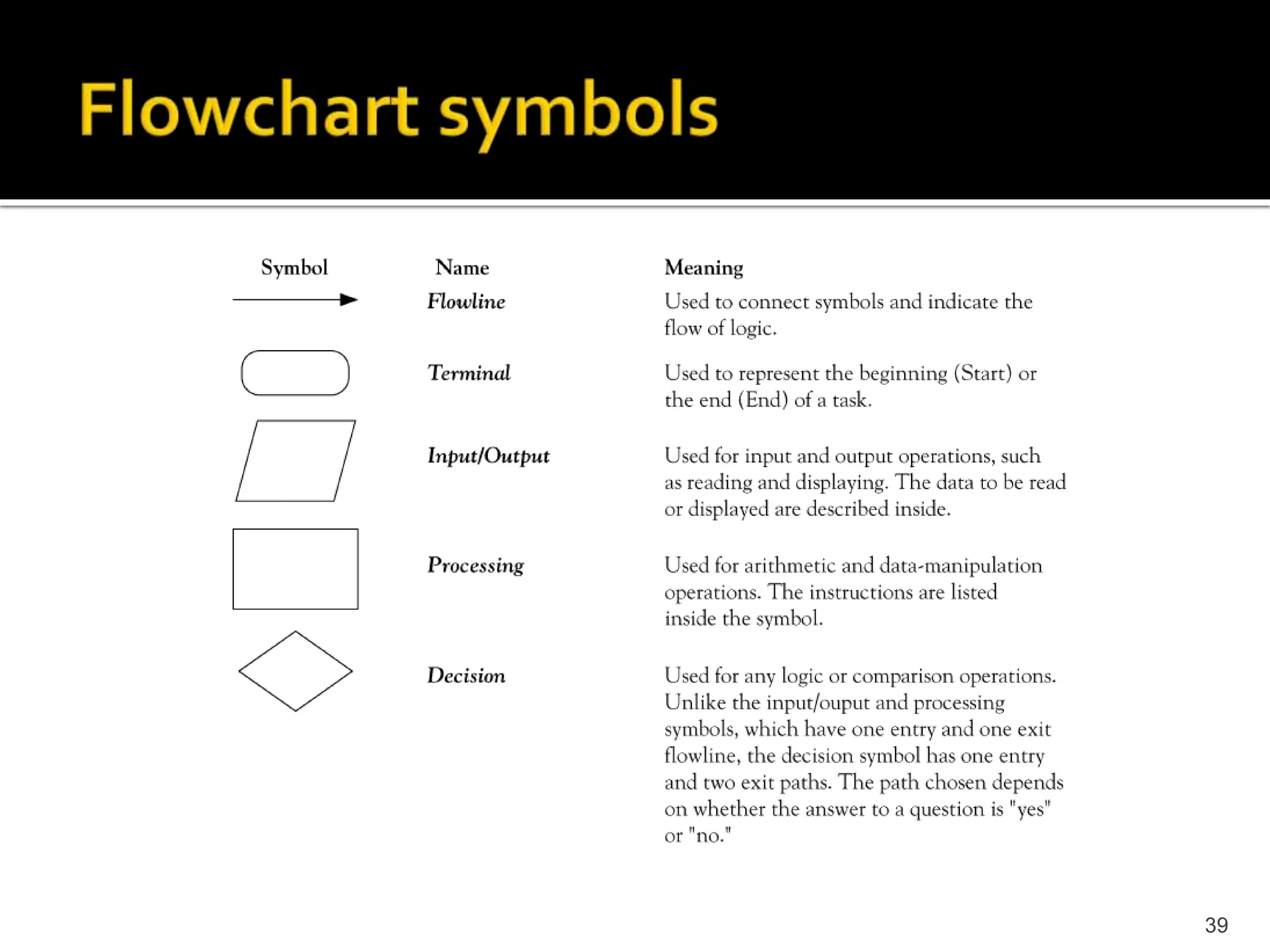
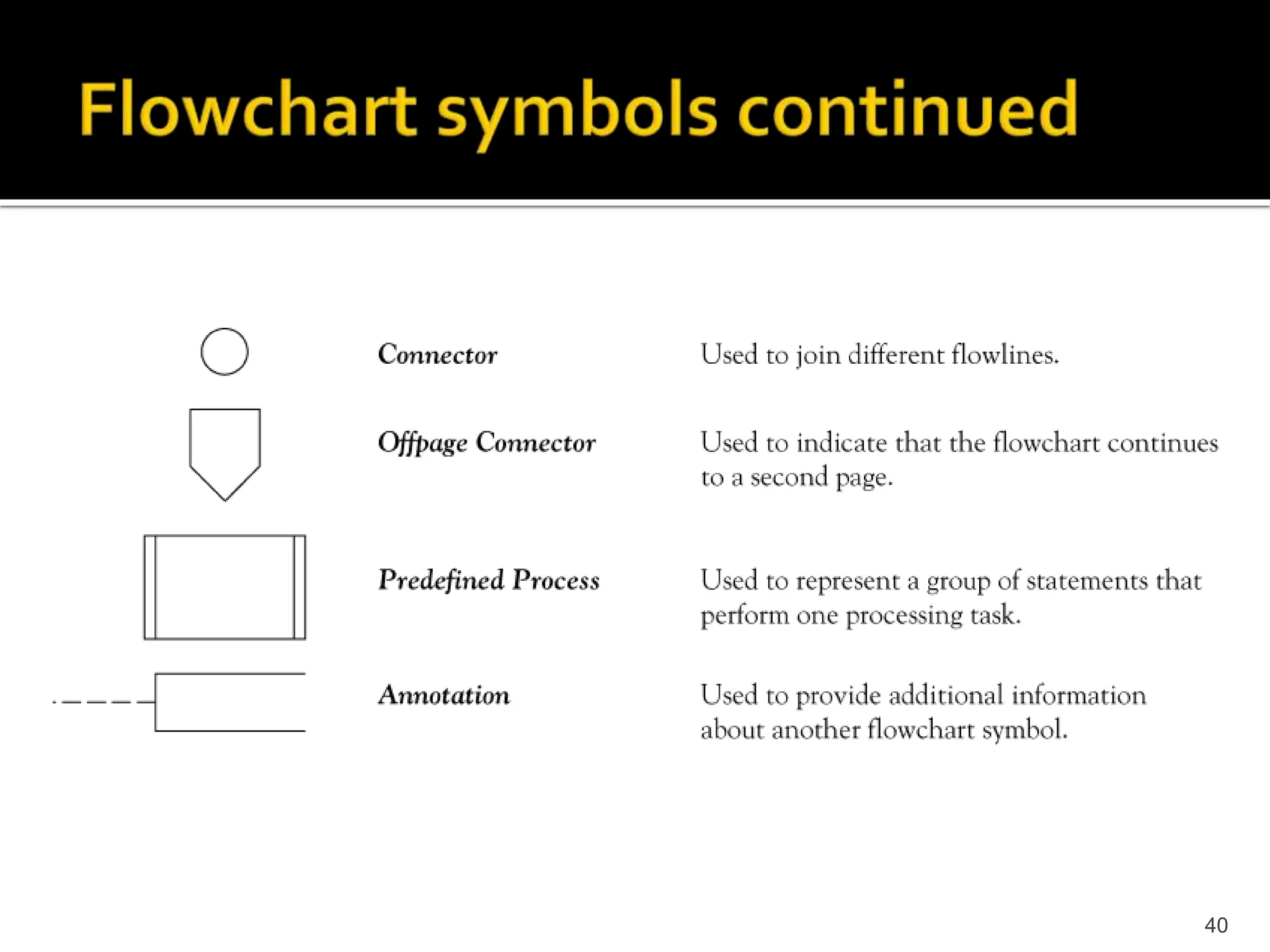
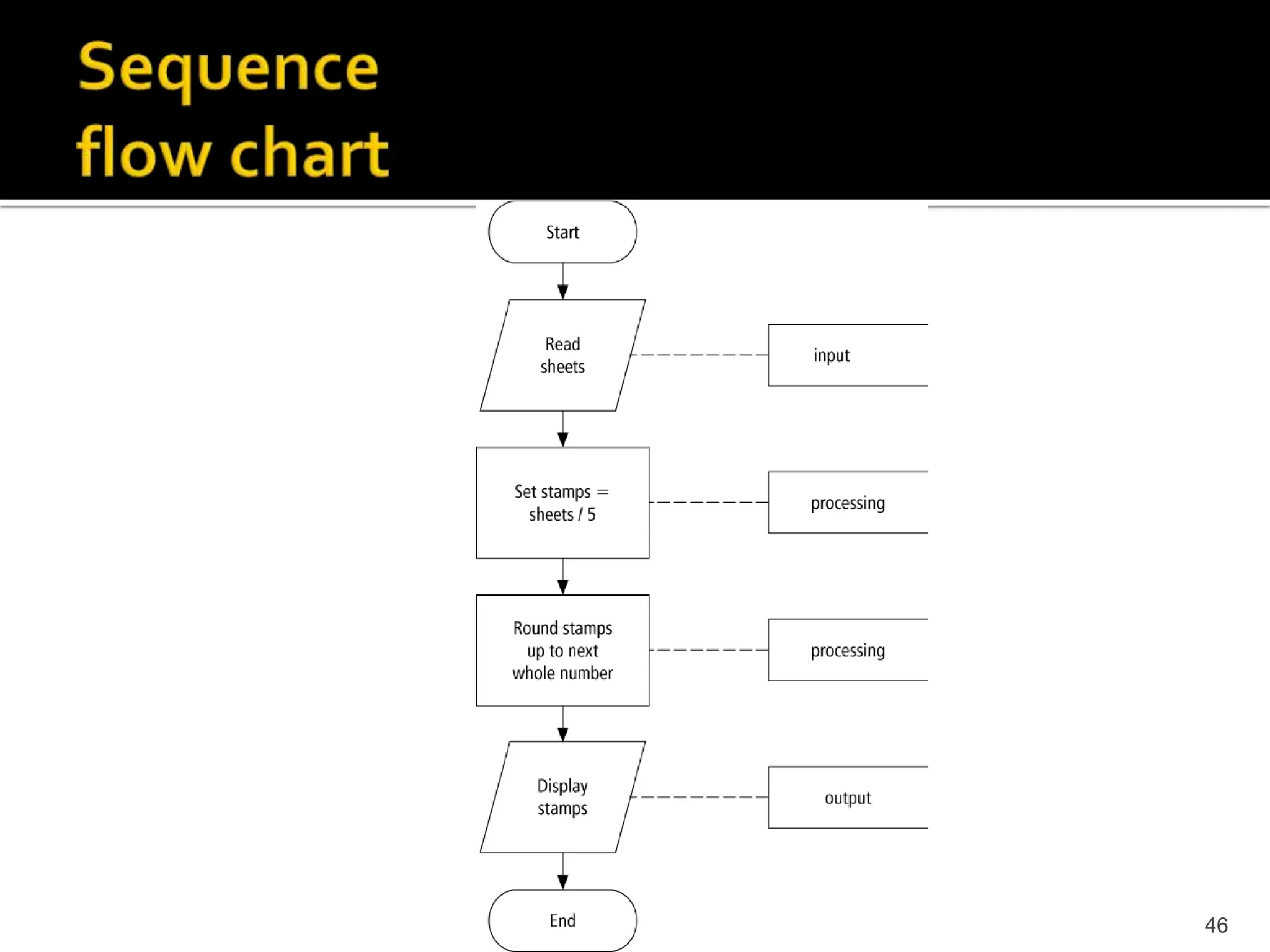
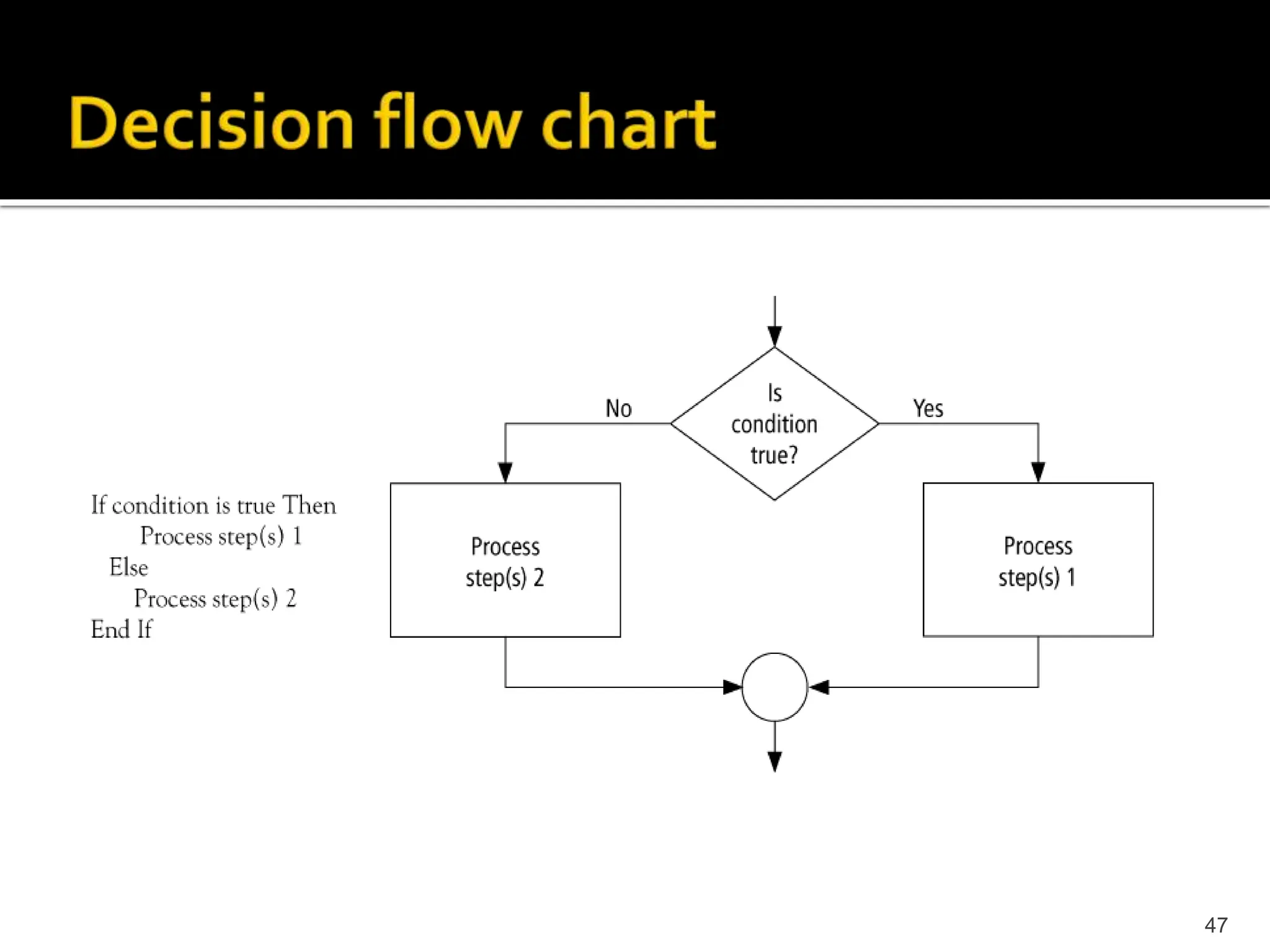
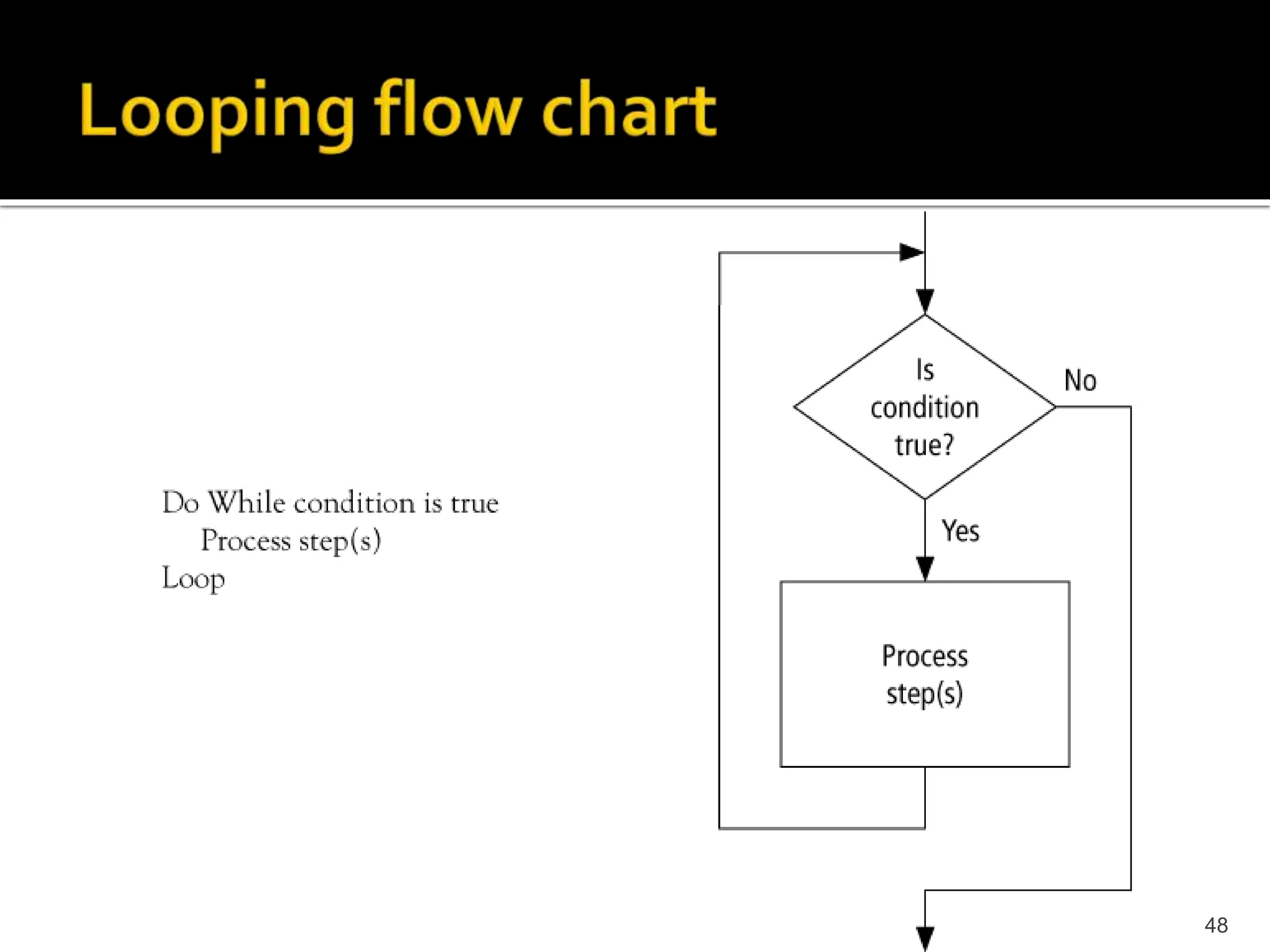
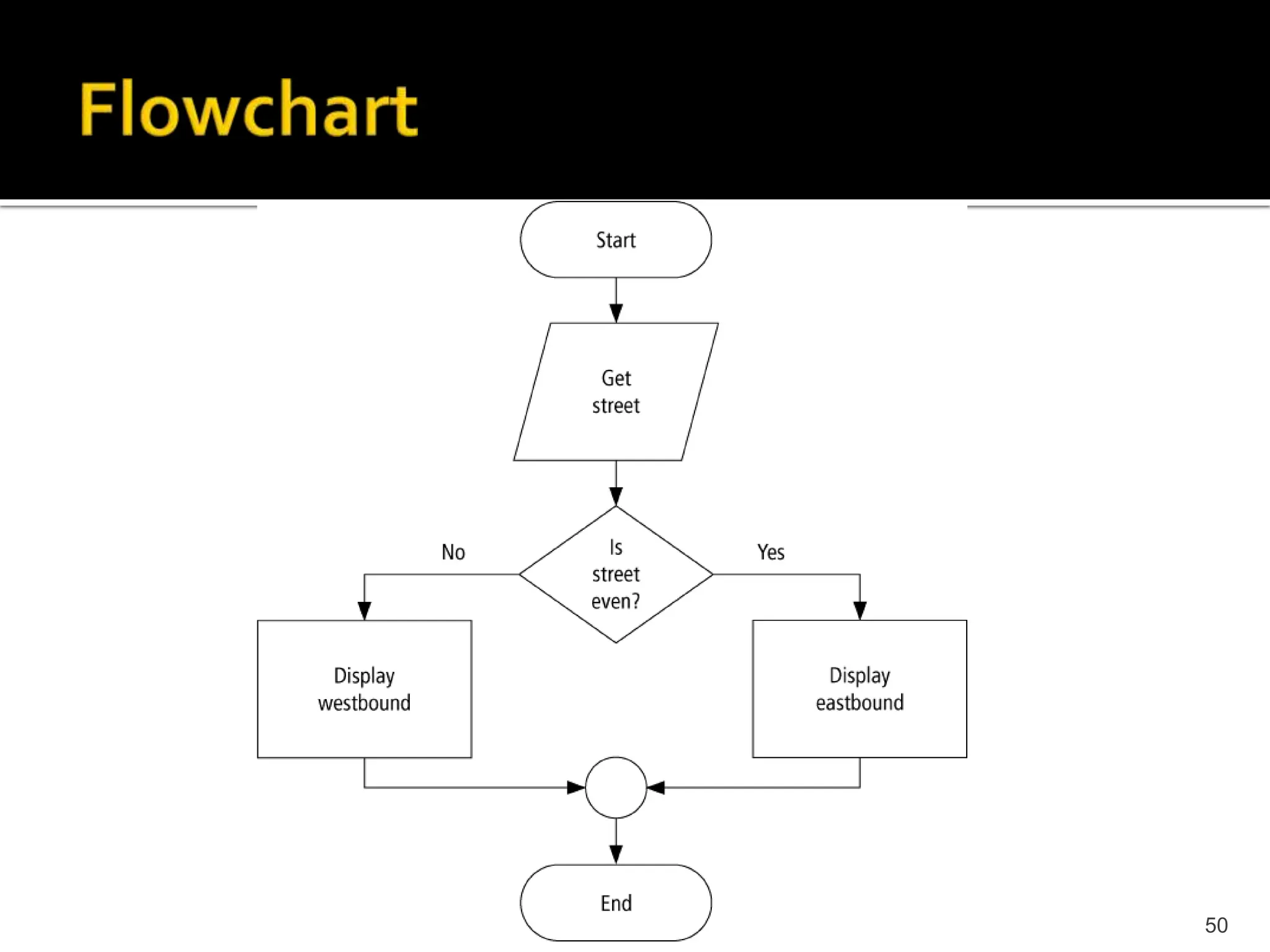
The document describes the basic components of a computer system, including hardware, software, input/output devices, memory, storage, and how binary language is used to represent data and instructions. It explains how programming languages are used to write programs that are then compiled or assembled into machine-readable code that can be executed by the computer's CPU. The problem solving process of understanding the problem, devising a solution, implementing and testing it is also summarized.