Fuzzy Genetic Algorithm Approach for Verification of Reachability and Detection of Deadlock in Graph Transformation Systems

Fuzzy Genetic Algorithm Approach for Verification of Reachability and Detection of Deadlock in Graph Transformation Systems

• 1.
  Presented by AmirMosavi Fuzzy Genetic Algorithm Approach for Verification of Reachability and Detection of Deadlock in Graph Transformation Systems
• 2.
  A.Chromosome Encoding In thepresented approach, the model checking system, instead of examining all of the state space in order to find the desired state, drives the search using the fuzzy genetic algorithm toward an optimal solution. The state space is a collection of states and transitions between them, which is depicted as a tree called a state space tree. Each possible solution is a path that starts from the initial node of the graph and specifies a chromosome. Each chromosome consists of a number of genes. In the proposed algorithm, named FGA, each gene is a random number that is generated between zero and the maximum number of output transmissions in the specified problem. Figure. 1 illustrates one example of an encoding scheme which represents a path in a graph by a vector. In this case, the chromosome is 1, 0, 2, 1. The sufficient length of the chromosomes is the depth of the search in the model checking, and since the solution of different case studies can be found at different depths, the length of chromosomes is considered as a variable. B.The Fitness Functions 1)Fitness Function for detecting deadlocks What needs to be checked to confirm the safety property is whether a desired property is satisfied on all paths and in all states of those paths or not. There is not any particular method to verify the safety property, but there are some solutions to refute this property. One of these events which can refute the safety property is occurring deadlock in the model. A promising solution corresponding with chromosome 1021 Methods
• 3.
  The membership functionof Δf The membership function of the input variabled(t-1) The membership function of ΔPm. Results
• 4.
  Fuzzy Genetic AlgorithmApproach for Verification of Reachability and Detection of Deadlock in Graph Transformation Systems Nahid Salimi Department of Computer Engineering, Faculty of Engineering, Arak University, Arak, Iran n-salimi@phd.araku.ac.ir Amir Mosavi 1,2* 1Kando Kalman Faculty of Electrical Engineering, Óbuda University Budapest, Hungary 2 School of Economics and Business Norwegian University of Life Sciences 1430 Ås, Norway amir.mosavi@kvk.uni-obuda.hu Vahid Rafe Department of Computer Engineering, Faculty of Engineering, Arak University, Arak, Iran v-rafe@araku.ac.ir Hamed Tabrizchi Department of Computer Science, Shahid Bahonar University Kerman, Iran 0000-0001-9250-2232 Abstract— model checking techniques are often used for the verification of software systems. Such techniques are accompanied with several advantages. However, state space explosion is one of the drawbacks to model checking. During recent years, several methods have been proposed based on evolutionary and meta-heuristic algorithms to solve this problem. In this paper, a hybrid approach is presented to cope with the SSE problem in model checking of systems modeled by GTS with an ample state space. Most of existence proposed methods that aim to verify systems are applied to detect deadlocks by graph transformations. The proposed approach is based on the fuzzy genetic algorithm and is designed to decline the safety property by verifying the reachability property and detecting deadlocks. In this solution, the state space of the system is searched by a fuzzy genetic algorithm to find the state in which the specified property is refuted/verified. To implement and evaluate the suggested approach, GROOVE is used as a powerful designing and model checking toolset in GTS. The experimental results indicate that the presented hybrid fuzzy method improves speed and performance by comparing other techniques. Keywords— fuzzy genetic algorithm, reachability property, deadlock, model checking, artificial intelligence I. INTRODUCTION Today, as computer use increases, software systems have found an important place in human life by implementing complex operations that are impossible to do. The increment of the using software systems leads to increase complexity. The security concern is an essential point in the development of software systems, especially in critical-safety systems, where errors would cause irrecoverable disasters. In critical- safety systems, even small mistakes can have irrecoverable consequences. Lots of financial and human damages have occurred due to programming errors in such systems, including the Ariane5 shuttle explosion, the loss of the Mars Climate Orbiter, and the overdosing patients during radiation due to errors in the radiation control section of the device. Model-checking techniques are applied as one of the most accurate automatic verification methodologies that are used to validate systems even before implementation and at the design phase [1]. The use of this technique requires a description for the system through a formal language [2]. One of the standard tools applied to design and model checking the methods specified via GTS is the GROOVE toolset, which performs model checking by generating the entire state space of the model. State space explosion occurs when the size of the model increases, the memory consumption increases exponentially. In recent years, several approaches have been proposed to resolve the problem of state-space explosion in the model checking of complex systems modeled by GTS. Some of these methods are a GA based solution [3], an approach using PSO algorithm, and also, an algorithm based on a hybrid of PSO and GSA [4], a method by using the combination of PSO and BAT optimization algorithm [5], an approach based on data mining methods named EMCDM [6], and an efficient solution through Bayesian optimization algorithm [7]. All of these solutions are presented to refute the safety property by finding the deadlock state in the systems specified through GTS. Notwithstanding the great efforts by various researchers to verify safety property in systems specified through graph transformations using detecting deadlocks, many aspects related to system verification are still unsolved. One of the properties which can be checked is the reachability property. In this study, a new approach based on the Fuzzy Genetic algorithm is proposed that includes two different fitness functions. The first one is applied to refute safety property by finding a deadlock state and the second one is presented to verify reachability property. The previous methods, proposed in this context, tried to detect deadlocks for ascertaining the safety property. In this paper, the suggested approach is used to refute safety property by verifying reachability property in the systems modeled via GTS, as well. The proposed method
• 5.
  has been implementedusing GROOVE, as a powerful designing and model checking toolset, and the Java programming language. The results of executing the proposed approach on several great case studies are presented and discussed. Comparing the reported results and those of other existing methods reveals the acceptable performance of the proposed solutions. This paper is organized as follows: Section 2 introduces the required backgrounds of the presented methods, such as the structure and concepts of fuzzy systems, the details of the fuzzy genetic algorithms, the graph transformation systems and the model checking concepts. The proposed approach to cope with the problem of the state space explosion is investigated in Section 3. Section 4 describes how to design and implement the proposed approaches. In section 5, the suggested solutions are evaluated and, the results are compared and discussed. Section 6 includes the performance evaluation, and eventually, Section 7 presents the conclusion of the paper and suggests some future researches. II. BACKGROUND A. Model Checking Model Checking is a formal method for verifying the correctness of the software systems even at design time. To use the model checking, it is required to describe the system’s features using a formal language [4]. The model checker automatically explores all the state space of the system and determines whether the given ownership of the system is satisfied or not. Some essential properties of a system that could be verified are the safety property, the reachability property, the liveness property, and the fairness property. Despite many benefits of the model checking, this technique also has some drawbacks, for which the state space explosion is the most important. B. Graph Transformation System GTS is a technique to model a system graphically based on a mathematical and formal method [2]. An attributed graph transformation system is specified through a triple: GTS = (TG, HG, R), Where TG is the type graph, HG is the host graph, and R stands for the rules. The type graph is the meta-model of the system represented by TG = (TGN, TGE, src, trg), in which TGN is a set of nodes, TGE is a set of edges and src, and trg are two functions that, respectively, assign a source and a destination to each edge: src, trg: TGE → TGN The host graph is a graph representing the initial state of the system. In other words, the host graph must be a graph morphism type graph [8]. A graph transformation rule is defined by a triple (LHS, RHS, NAC), where the LHS, which is a graph morphism TG, describes the pre-conditions of the rules, the RHS, which is a graph morphism TG, describes the post-conditions of the rules, and NAC is a special configuration which is used to verify the non-existence of a subgraph in the rule. The rule can be applied if NAC does not exist in the host graph [8]. C. Fuzzy Inference System Fuzzy logic is a mathematical-based representation of human knowledge and experiences that was introduced by Zadeh in 1968 [9]. A FLC consists of a Knowledge Base that encodes the expert knowledge using a set of IF-THEN rules. An IF-THEN rule is a conditional statement with the form: If a set of conditions is satisfied, then a set of consequences can be inferred [10]. A fuzzy system is composed of three basic parts: the fuzzification process, fuzzy inference system (FIS), and defuzzification process. •The fuzzification part includes the definition of the linguistic variables regarding inputs and outputs. •The inference system includes the definition of rules that aim to describe the system and also a mapping from input to output using defined rules. In fact, types of fuzzy inference systems [11] divided into two types called Mamdani’s fuzzy systems inference method and Sugeno-type fuzzy systems inference method [12]. The vivid difference between these methods is their final output. The output of Sugeno ought to be constant or linear, while the Mamdani type expects the output membership functions to be fuzzy sets. In fuzzy logic, imprecise values are represented by a fuzzy set that is described through a membership function.In fact, this function determines a degree ∈ [0, 1] to every number x ∈ X. The membership functions for the state variables can be triangular, Gaussian, trapezoidal or bell- shaped. D. The Genetic Algorithm The genetic algorithm was first introduced by John Haled in 1975 and then generalized by John Koza in 1992. The main idea of the genetic algorithm is Darwin's theory of evolution. The genetic algorithm has four main elements: Initial population, fitness function, selection, and genetic operators. Crossover and mutation are two genetic operators that are used to produce a new generation. The genetic algorithm is an iteration-based algorithm, which creates several random solutions (chromosomes) in the first step and generates new chromosomes from the previous population in the next steps. In each generation, some of the most appropriate solutions are selected to remain. Then, the next generation will be produced by crossover and mutation operations on selected chromosomes. This process repeats until one of the chromosomes is the desired solution, or the algorithm iteration is equal to the predefined maximum generation, or the best fitness value of the population does not improve over several successive generations [13]. E. Fuzzy Genetic Algorith In the standard genetic algorithm, there are three parameters necessary to be assigned with the appropriate value at the beginning of the algorithm to find an optimum solution. These parameters are as follows: Crossover Rate: percentage of the chromosomes which are chosen in each iteration for crossover operation and generate new chromosomes. Mutation Rate: percentage of the chromosomes which are mutated in each iteration. Population Size: the number of chromosomes in each generation. For example, when Population Size is small, the algorithm covers a small part of the problem space, and no good result will be achieved. While this parameter is
• 6.
  significant, the geneticalgorithm goes slowly, and it takes a long time to solve and optimize the problem [14]. Selecting an appropriate value for algorithm parameters is one of the challenges of applying the genetic algorithm. In a fuzzy genetic algorithm, these parameters are evaluated in each iteration of a genetic algorithm through a fuzzy inference system. However, so many types of fuzzy systems are presented to determine the genetic algorithm parameters. In most of these FS, parameters such as age of chromosomes, fitness function ratio of generation, the difference between fitness of two recent generations, the difference between fitness of each chromosome and average fitness of the total population, the average fitness of the previous generation and present generation, the difference between fitness of two generations for each chromosome, the difference between maximum fitness and average fitness of a generation, etc. are considered as the input of the fuzzy system. Also, in most of the recommended fuzzy systems (more than 99%), crossover rate and mutation rate are the outputs of the fuzzy system. III. RELATED WORKS There are various solutions having been proposed in order to improve model checking techniques verifying complex systems and dealing with a specific problem called the state space explosion problem. There are two well-known meta- heuristic approaches that have been intended to discover deadlocks in the methods and refute the security property are a framework based on reinforcement learning [15] and an ant colony algorithm [16-18]. A new approach has been proposed using the genetic algorithm for checking the correctness of communication protocols in [19]. This genetic validation has been tried on the Transmission Control Protocol and on a hand-made contract. In [20] two different learning algorithms have been proposed to verify safety, reachability, and liveness properties of systems whose state space can be expressed using regular expressions. In the other paper, an ACO-based approach aiming to decrease the state explosion problem for discovering deadlocks in complex networks is presented. In fact, this approach describes a way that uses the Calculus of Communicating Systems [21]. Two other papers [22, 23] proposed using a type of ACO model to disprove safety and liveness attributes in concurrent systems [3]. This approach applies the GA algorithm on several random paths with a particular length that starts from the initial state and finds the first path, which leads to a deadlock state. GROOVE toolset is used to implement this solution in order to evaluate its performance. The other proposed approach for this problem uses the PSO algorithm to detect deadlocks in graph transformation systems [4]. The authors have also suggested a hybrid algorithm based on PSO, and GSA named PSO-GSA to avoid the local optima problem. Authors of [5] suggested a hybrid solution based on particle swarm optimization algorithm and a Bat algorithm called BAPSO to solve the state space explosion problem for detecting deadlocks in systems modeled via graph transformation. In this approach, the Bat algorithm is used to avoid the local optima problem in PSO. Another solution using a simple greedy algorithm called BFA is also proposed in this paper in which a state with the minimum outgoing transitions must be selected in each step of exploration. These two approaches are implemented in the GROOVE. In [6] a method is presented based on data mining approaches called EMCDM. This method aims to fulfill the process of model checking in complex software systems that are designed according to a specific architectural style (specified via GTS). The EMCDM approach aims to decline the safety property by verifying the reachability property. In the other research [7], three BOA-based methods (nBOA, tpBOA, and cBOA) are presented deadlocks detecting way in systems that are modeled by graph transformations. The results of this algorithm indicate a noticeable improvement in speed and accuracy. IV. THE PROPOSEDAPPROACH A. Chromosome Encoding In the presented approach, the model checking system, instead of examining all of the state space in order to find the desired state, drives the search using the fuzzy genetic algorithm toward an optimal solution. The state space is a collection of states and transitions between them, which is depicted as a tree called a state space tree. The main goal is to discover the desired state in which the specified property is verified or refuted. Each solution is a sequence of states in the state space that starts from an initial state and traverses a set of states and transitions to reach this final state. In this approach, a fuzzy genetic algorithm has been used to find the optimal path that is ended with the desired state. Each possible solution is a path that starts from the initial node of the graph and specifies a chromosome. Each chromosome consists of a number of genes. In the proposed algorithm, named FGA, each gene is a random number that is generated between zero and the maximum number of output transmissions in the specified problem. Figure. 1 illustrates one example of an encoding scheme which represents a path in a graph by a vector. In this case, the chromosome is 1, 0, 2, 1. The sufficient length of the chromosomes is the depth of the search in the model checking, and since the solution of different case studies can be found at different depths, the length of chromosomes is considered as a variable. B. The Fitness Functions 1) Fitness Function for detecting deadlocks What needs to be checked to confirm the safety property is whether a desired property is satisfied on all paths and in all states of those paths or not. There is not any particular method to verify the safety property, but there are some solutions to refute this property. One of these events which can refute the safety property is occurring deadlock in the model. Figure 1. A promising solution corresponding with chromosome 1021
• 7.
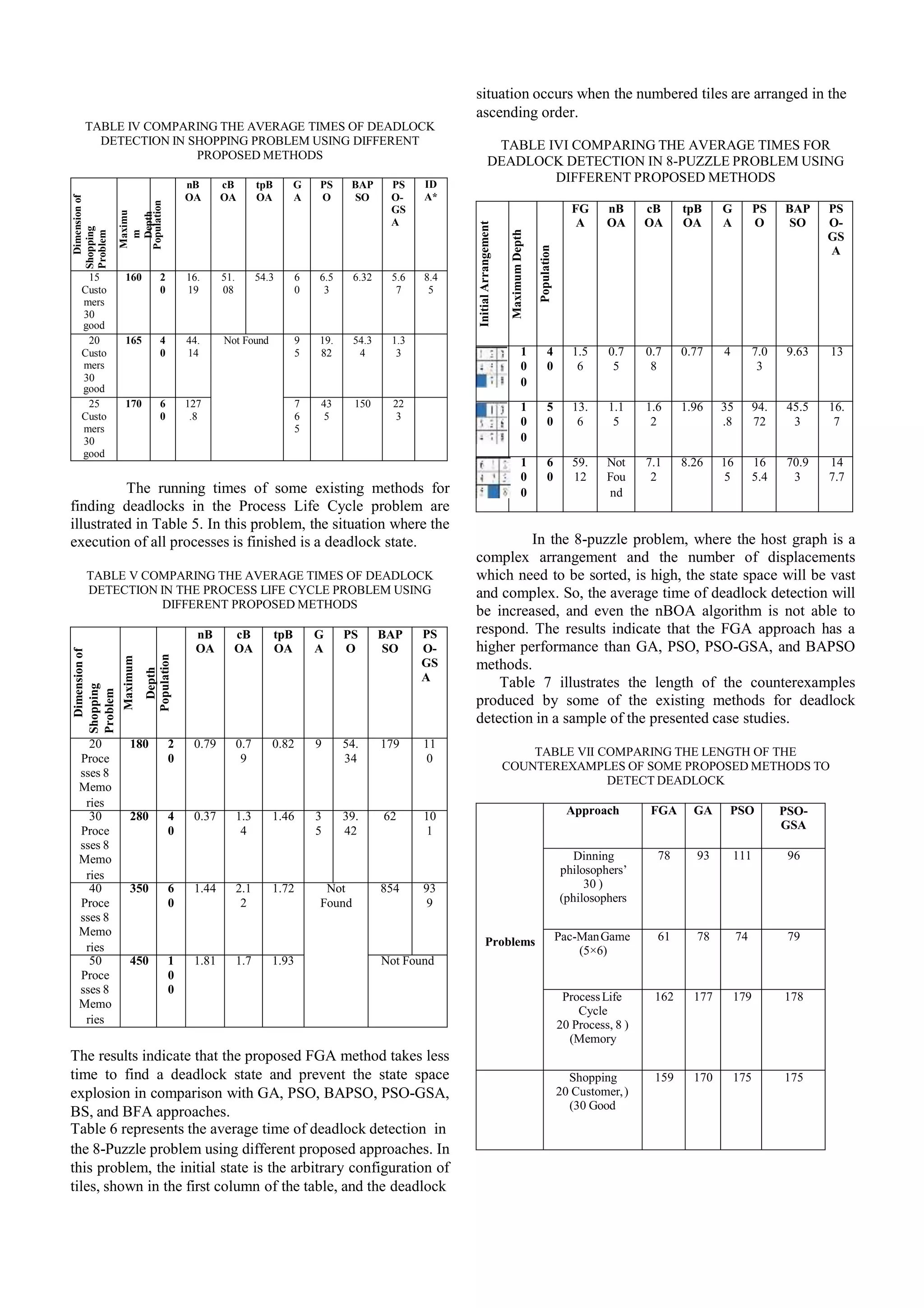
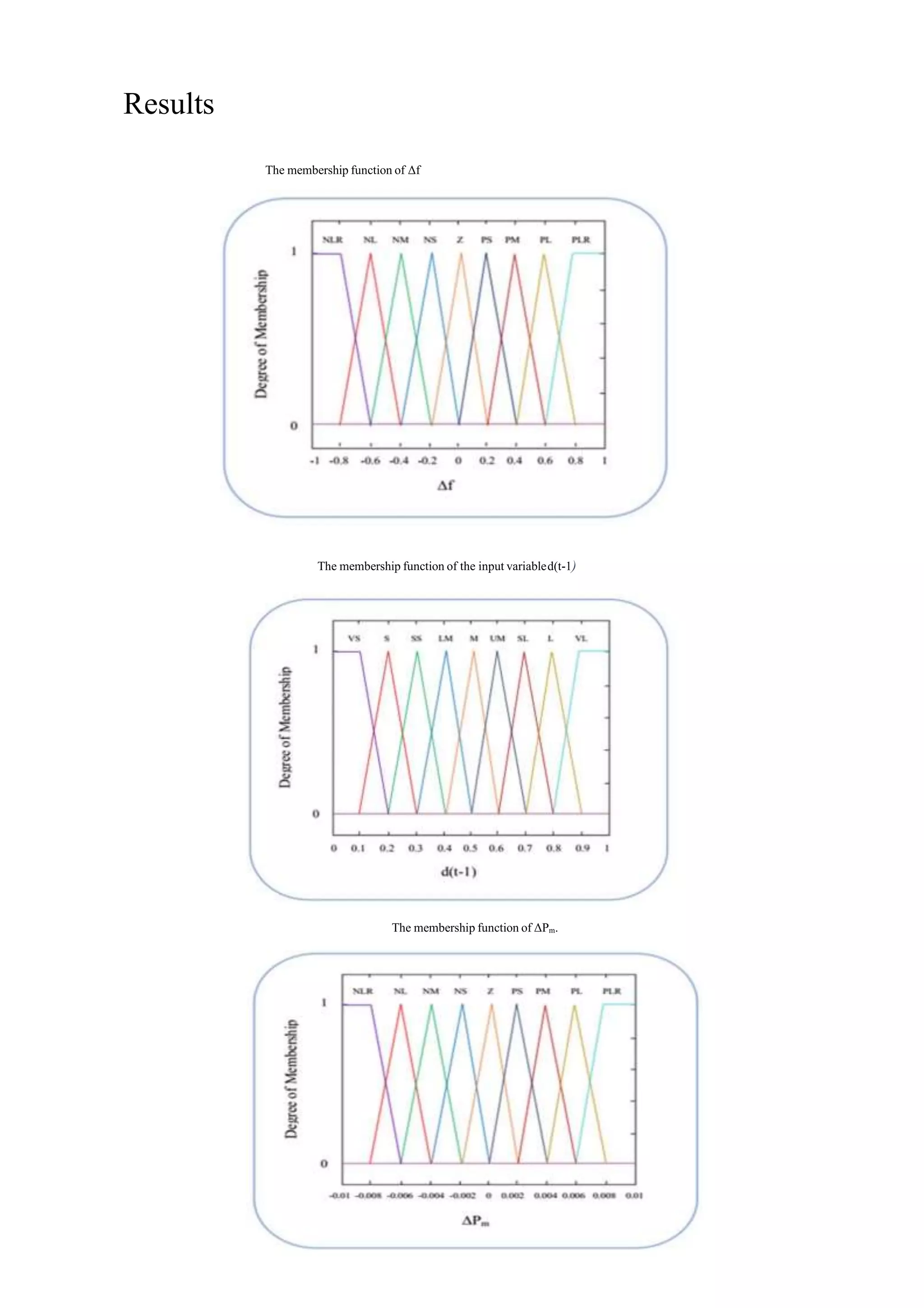
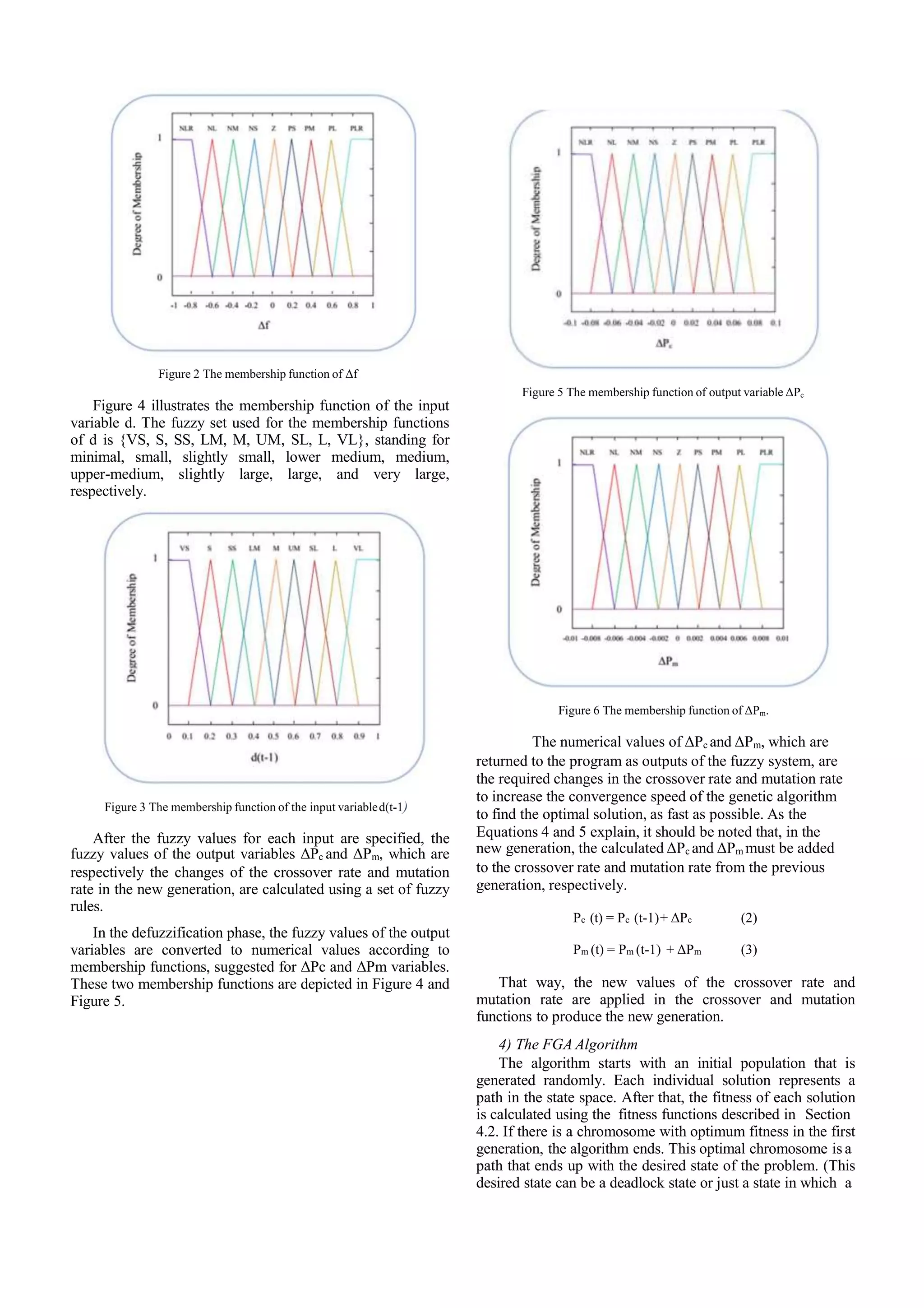
  Deadlock is astate with no output edges, so we can use the strategy presented in [3] to calculate the fitness function of a genetic algorithm. Consequently, the evaluation function, which used to detect a deadlock, is equal to the sum of the number of outputs having traveled through a path. The reason for choosing this method is that as the number of outputs of a path is lower, the probabilities of reaching the deadlock increase. Equation (1) shows this fitness function. L F(x) = Σ ni (1) i=1 Where L is the length of the path x, and ni is the total number of outputs in-depth i. A path with less value of fitness function has more likely to reach the deadlock. 2) Fitness Function to Verify the Reachability Property To examine the reachability property, it is vivid that a particular event happens at least once in the system. One state might be reachable if there is at least one path from the initial state to it. Consequently, there must be a path from the initial state that leads to the desired state. Furthermore, a path whose last state is quite similar to the specified reachability property can be a promising path, which may quickly reach the solution. For this reason, to verify this property, we use a similarity function that calculates the similarity between the given property and the last state of the path is represented by the individual solution (chromosome). A path whose final state has more similarity to the specified property will be a promising path, and tracing it will increase the probabilities of reaching the desired state. The proposed fitness function presented in Algorithm 1. Algorithm 1. Fitness function to verify the reachability property 1. Input & Output: a. Input: h: a particle and p: a given reachability property to be checked; b. Output: the fitness value of h; 2. Initialization: a. Initialize NodeList member Npi with node ith of Gp; b. Initialize EdgeList member Epi with node ith of Gp; c. Initialize NodeList member Nhi with node ithof Gh; d. Initialize EdgeList member Ehi with node ith of Gh; e. Initialize BooleanList member hVisitedij with false; f. Initialize BooleanList member pVisitedij with false; g. Initialize BooleanList member Visitedij with false; (For part e, f and g: i: 0 to Number of nodes Gh, j: 0 to Number of nodes Gp) 3. for each Nhi for each Npj EdgeList ENP = all edges of Ep whose source node is Npj; EdgeList ENH = all edges of Eh whose source node is Nhi; E-Countij = The number of pairs (p,h) which (p) is from ENP and (h) is from ENH as p’s label is equal to h’s label; PE-Countij = size of ENP; DE-Countij = E-Countij –PE-Countij; en d for end for 4. EQ-Count = 0; while all Visitedij is not true do Find the smallest DE-Countij thatVisitedij = false; Visitedij = true; if !pVisitedij && !hVisitedij then EQ-Count += E-Countij; pVisitedij = true; hVisitedij = true; end if end while 5. Find all NACs of Gp and store in ArrayList of NACs allNAC NEQ-Count = 0; for each NACi in allNAC do NEQ-Count += The number of nodes and edges of NACi occurring in Gh; end for return EQ-Count – NEQ-Count; 3) The Fuzzy Systems Proposed to Estimate Crossover and Mutation Rates Assigning the appropriate initial parameters is one of the challenges to use the standard genetic algorithm that can affect the efficiency of the algorithm. If the parameters like the crossover and mutation rates are initialized by inappropriate values, it would be difficult to find the best solution. The fuzzy system presented in the FGA-based method is a Mamdani fuzzy system derived from [24] that determines the variation which is required for the two parameters of the crossover and mutation rate in each iteration of the algorithm. The input variables of this fuzzy system are the degree of difference between chromosome fitness for two successive generations (Δf) and the diversity degree of the population in the previous generation (d (t-1)) that are obtained from Equations (2) and (3), respectively.
• 8.
  Figure 2 Themembership function of Δf Figure 4 illustrates the membership function of the input variable d. The fuzzy set used for the membership functions of d is {VS, S, SS, LM, M, UM, SL, L, VL}, standing for minimal, small, slightly small, lower medium, medium, upper-medium, slightly large, large, and very large, respectively. Figure 3 The membership function of the input variabled(t-1) After the fuzzy values for each input are specified, the fuzzy values of the output variables ΔPc and ΔPm, which are respectively the changes of the crossover rate and mutation rate in the new generation, are calculated using a set of fuzzy rules. In the defuzzification phase, the fuzzy values of the output variables are converted to numerical values according to membership functions, suggested for ΔPc and ΔPm variables. These two membership functions are depicted in Figure 4 and Figure 5. Figure 5 The membership function of output variable ΔPc Figure 6 The membership function of ΔPm. The numerical values of ΔPc and ΔPm, which are returned to the program as outputs of the fuzzy system, are the required changes in the crossover rate and mutation rate to increase the convergence speed of the genetic algorithm to find the optimal solution, as fast as possible. As the Equations 4 and 5 explain, it should be noted that, in the new generation, the calculated ΔPc and ΔPm must be added to the crossover rate and mutation rate from the previous generation, respectively. Pc (t) = Pc (t-1)+ ΔPc (2) Pm (t) = Pm (t-1) + ΔPm (3) That way, the new values of the crossover rate and mutation rate are applied in the crossover and mutation functions to produce the new generation. 4) The FGA Algorithm The algorithm starts with an initial population that is generated randomly. Each individual solution represents a path in the state space. After that, the fitness of each solution is calculated using the fitness functions described in Section 4.2. If there is a chromosome with optimum fitness in the first generation, the algorithm ends. This optimal chromosome is a path that ends up with the desired state of the problem. (This desired state can be a deadlock state or just a state in which a
• 9.
  specified reachability propertyis fulfilled). Otherwise, the values of the variables d (t-1) and Δf are calculated according to Equations 2 and 3 and are transmitted as inputs to the fuzzy system. In the fuzzy system, the optimal values of the crossover rate and mutation rate, calculated using the membership functions and the fuzzy rule base, which presented in 4.3, are sent to the genetic algorithm. The algorithm continues with creating a new generation of chromosomes by applying the crossover and mutation operations. Several chromosomes, which are selected by Elitism selection, are transferred to the new generation without any changes. In Elitism selection, the best chromosomes, according to their fitness function values, are selected. Depending on the crossover rate, a pair of chromosomes is selected to participate in the crossover operation. A truncation selection method is used to select the pair of chromosomes. This selection method is similar to the roulette wheel method, with the difference that the rate of selection is fixed during the execution. The applied crossover operation is a single-point. Through the mutation operation, some chromosomes are selected, according to mutation rate, calculated by the fuzzy system. The genes of the selected chromosome are randomly picked out and replaced by newly generated random values. After calculating the fitness value of the new generation chromosomes, if the chromosome, which indicates the path leading to the desired state of the problem, is found or the number of generations is equal to the specified maximum generation, the algorithm is finished; otherwise, the algorithm continues by calculating the input parameters of the fuzzy system. Fig. Seven illustrates how a fuzzy genetic algorithm works. Figure 7 The Flowchart of Fuzzy Genetic Algorithm V. THE PROPOSED APPROACH IMPLEMENTATION The suggested approach is implemented in GROOVE toolset using Java programing language. To implement the proposed method, some new classes have been added to the packages, and some classes have been modified. The proposed algorithm leads the model checker to find the specified state optimally. In this work, the search space, which should be explored, is the state space of a system. This state-space starts from an initial state. In implementing the algorithm and in all the experiments, the number of algorithm iteration is 100 and the crossover location is considered in the middle of the chromosome. Two other parameters, which are used to implement these two solutions, are the number of the initial population and the length of the chromosomes or the search depth. These parameters have been changed according to the variation of the case study dimension, and the optimum values for these tow parameters are applied to generate the results. The suggested methods are tested on several well-known case studies in which the model checking is faced with the problem called space state explosion. In addition, during the process of evaluation, the size of the model witness increases. The experiments are performed by using a 3GB memory and an Intel CORE i5 (2.2GHz) processor. A. Dinning philosopher’s problem The dining philosophers’ problem is the problem of some philosophers that sitting on every side of a table. In fact, there is one fork between every two adjoining philosophers. Furthermore, a philosopher is thinking and then gets hungry, picks up the left fork, and next to the right one. When a philosopher who has two forks starts eating, each hungry philosopher can only eat when philosopher who starts eating has both left and right forks. He then stop eating and the process is repeated infinitely until the deadlock state happens in which all philosophers take the left fork and wait for the right one [25]. B. Pac-Man game problem The Pac-Man game includes three objects: ghosts, Pac- Man, and marbles [8]. In each stage the Pac-Man and the Ghost proceed to an adjacent box. In a new box he eats the marble. The ghost may kill Pac-Man if find it in an adjacent box. The game will finish when all marbles are eaten or Pac- Man is killed by a ghost. C. Car Platoon problem Car Platoon system [27] includes multiple cars that moving in a highway with a constant speed and invariant distance of each other. Among these cars, there is one leader car called a follower. A property that ought to be checked in this system is that a channel should not be created between two followers. In other words, if one free car (a car that is not a member of the platoon system) sends a demand for creating a channel to a follower, never should it receive the acceptance. Also, a follower should not request to create a channel to another follower, and the request should not be from the leader. If one of these states happens, the deadlock will happen. D. Process Life Cycle problem The problem called Process Life Cycle describes the stages of the life cycle, which traverses in the operating system. In the first stage, a new process is created. The life cycle continues with loading the new process into memory. If there is enough free memory. Then, after loading the process in the memory, it should wait to use CPU or I/O devices. When the process is executed entirely, all resources allocated to the process are released, and the process stops. E. Shopping problem This problem explains the shopping process in a shop by customers presented in [28]. In this problem, some customers who are in a store start their shopping by taking a shopping cart, pick up items from shelves, and put them in a cart. They pay the price of the selected items and empty the cart. So, their shopping process will be finished. In this problem, the deadlock state will happen when all customers finish their shopping successfully.
• 10.
  F. 8-Puzzle Problem 8-puzzleproblem is a problem that can be solved by configuration and arrangement. In fact, there is a board with nine boxes filled with eight numbered tiles from 1 to 8 and one empty box [29]. Each tile can move to an empty box if the empty cell is adjacent to it. The goal of the game beginning with an arbitrary configuration of tiles and arrange the numbers in the ascending order. VI. PERFORMANCEEVALUATION A. FGA Approach to detect deadlock The results of applying the suggested approach to refute safety property through deadlock detection are compared with those of DFS and BFS, which are primary strategies of model checking by GROOVE toolset. The results also are compared with other proposed approaches based on BS, IDA*, Genetic Algorithm, PSO, PSO-GSA, BAPSO, BFA, ECDM, and BOA. The presented results in these comparisons show the average deadlock detection time for 20 runs. The FGA algorithm performance comparison with other presented algorithms is illustrated in Tables 3 to 8 for deadlock detecting in dining philosophers, Pac-Man game, car platoon, 8-puzzle, process life cycle, and shopping problems, respectively. According to the results, the average running time of the proposed algorithm in dining philosophers is better in comparison with those of GA, PSO, PSO-GSA, and BAPSO algorithms. The FGA algorithm performance comparison with other algorithms for the dining philosophers’ problem is illustrated in Table 1. In this problem, the deadlock situation is the state in which philosophers have taken the left fork and are waiting for the right one. TABLE I COMPARING THE AVERAGE TIMES OF DEADLOCK DETECTION IN DINING PHILOSOPHERS’ PROBLEM USING DIFFERENT PROPOSED METHODS Numberof Maximu m Depth Population nB OA cB OA tpB OA GA PS O BAP SO PS O- GS A 8 20 1 0 0.61 0.85 0.72 3.1 6 3.5 7 2.31 4.1 3 1 0 25 1 5 0.71 1.29 0.93 10. 12 13. 45 8.34 38. 92 2 0 100 2 0 1.04 3.25 3.53 23 157 64.6 170 Results indicate that the FGA Approach produces better results than other approaches except for BOA-based solutions and BFA to detect deadlocks in dining philosophers’. Table 4 displays the average time of detecting deadlocks in the Pac-Man Game problem for some proposed approaches. In this problem, a deadlock state occurs when Pac-Man eats all the marbles, or the ghost kills Pac-Man. The results of the Pac-Man problem indicate that the FGA algorithm reduces the average time of detecting deadlocks in comparison with GA, PSO, BAPSO, PSO-GSA, IDA*, and BS methods. TABLE II COMPARING THE AVERAGE TIMES OF DEADLOCK DETECTION IN PAC-MAN GAME PROBLEM USING DIFFERENT PROPOSED METHODS Dimensionof Pac-man Game Maximu m Depth Population nBO A cBO A tpB OA G A PS O BAP SO PS O- GS A 4×4 100 40 1.03 1.6 1.8 1.0 3 2.6 1.3 1.9 4×5 100 60 0.72 0.7 0.73 1.1 2 4.9 2.8 4.7 5×6 100 80 0.77 0.83 0.92 1.3 2 11. 7 7.9 14. 5 The experimental results of applying the FGA method for deadlock detection in the Car Platoon problem are depicted in Table 3. TABLE III COMPARING THE AVERAGE TIMES OF DEADLOCK DETECTION IN CAR PLATOON PROBLEM USING DIFFERENT PROPOSED METHODS NumberofCars Maximu m Depth Population nB OA cBO A tpB OA G A PS O BAP SO PS O- GS A 1 0 100 20 0.38 0.37 0.36 0.3 6 2.6 5 5.43 2.6 5 2 0 100 40 0.42 0.44 0.42 0.4 3 7.0 3 9.45 5.7 8 3 0 100 60 0.45 0.47 0.47 0.5 6 14. 56 18.45 12. 63 4 0 100 80 0.54 0.55 0.58 0.7 8 20. 54 22.46 21. 45 5 0 100 10 0 0.69 0.7 0.69 1.1 8 30. 9 31.65 32. 51 According to the results of the Car Platoon problem, it is vivid that the time of finding deadlock is deficient in all methods except the BS approach because different paths end with a deadlock state. Based on table 3, the average time to detect deadlock of the FGA method in the Car Platoon problem is less than the results of other approaches except for BOA-based methods. Table 4 depicts the average time of deadlock detection in Shopping problems for different existing methods. In this problem, the deadlock state happens when all customers finish their shopping successfully. In the Shopping problem, it can be realized that the response time of all methods increases according to the increment of customers. Unlike the cBOA, tpBOA, BFA, BS, and IDA* methods, the FGA method does not face with the state space explosion even in models with an ample state space.
• 11.
  TABLE IV COMPARINGTHE AVERAGE TIMES OF DEADLOCK DETECTION IN SHOPPING PROBLEM USING DIFFERENT PROPOSED METHODS Dimensionof Shopping Problem Maximu m Depth Population nB OA cB OA tpB OA G A PS O BAP SO PS O- GS A ID A* 15 Custo mers 30 good 160 2 0 16. 19 51. 08 54.3 6 0 6.5 3 6.32 5.6 7 8.4 5 20 Custo mers 30 good 165 4 0 44. 14 Not Found 9 5 19. 82 54.3 4 1.3 3 25 Custo mers 30 good 170 6 0 127 .8 7 6 5 43 5 150 22 3 The running times of some existing methods for finding deadlocks in the Process Life Cycle problem are illustrated in Table 5. In this problem, the situation where the execution of all processes is finished is a deadlock state. TABLE V COMPARING THE AVERAGE TIMES OF DEADLOCK DETECTION IN THE PROCESS LIFE CYCLE PROBLEM USING DIFFERENT PROPOSED METHODS Depth Dimensionof Shopping Problem Maximum Population nB OA cB OA tpB OA G A PS O BAP SO PS O- GS A 20 180 2 0.79 0.7 0.82 9 54. 179 11 Proce 0 9 34 0 sses 8 Memo ries 30 280 4 0.37 1.3 1.46 3 39. 62 10 Proce 0 4 5 42 1 sses 8 Memo ries 40 350 6 1.44 2.1 1.72 Not 854 93 Proce 0 2 Found 9 sses 8 Memo ries 50 450 1 1.81 1.7 1.93 Not Found Proce 0 sses 8 0 Memo ries The results indicate that the proposed FGA method takes less time to find a deadlock state and prevent the state space explosion in comparison with GA, PSO, BAPSO, PSO-GSA, BS, and BFA approaches. Table 6 represents the average time of deadlock detection in the 8-Puzzle problem using different proposed approaches. In this problem, the initial state is the arbitrary configuration of tiles, shown in the first column of the table, and the deadlock situation occurs when the numbered tiles are arranged in the ascending order. TABLE IVI COMPARING THE AVERAGE TIMES FOR DEADLOCK DETECTION IN 8-PUZZLE PROBLEM USING DIFFERENT PROPOSED METHODS InitialArrangement MaximumDepth Population FG A nB OA cB OA tpB OA G A PS O BAP SO PS O- GS A 1 4 1.5 0.7 0.7 0.77 4 7.0 9.63 13 0 0 6 5 8 3 0 1 5 13. 1.1 1.6 1.96 35 94. 45.5 16. 0 0 6 5 2 .8 72 3 7 0 1 6 59. Not 7.1 8.26 16 16 70.9 14 0 0 12 Fou 2 5 5.4 3 7.7 0 nd In the 8-puzzle problem, where the host graph is a complex arrangement and the number of displacements which need to be sorted, is high, the state space will be vast and complex. So, the average time of deadlock detection will be increased, and even the nBOA algorithm is not able to respond. The results indicate that the FGA approach has a higher performance than GA, PSO, PSO-GSA, and BAPSO methods. Table 7 illustrates the length of the counterexamples produced by some of the existing methods for deadlock detection in a sample of the presented case studies. TABLE VII COMPARING THE LENGTH OF THE COUNTEREXAMPLES OF SOME PROPOSED METHODS TO DETECT DEADLOCK Problems Approach FGA GA PSO PSO- GSA Dinning philosophers’ 30 ) (philosophers 78 93 111 96 Pac-ManGame (5×6) 61 78 74 79 ProcessLife Cycle 20 Process, 8 ) (Memory 162 177 179 178 Shopping 20 Customer,) (30 Good 159 170 175 175
• 12.
  8-Puzzle Second ) (Arrangement 8 1311 10 It is totally vivid that the proposed FGA method decreases the length of counterexamples provide to refute safety property in all case studies. VII. CONCLUSIONS In this research, a hybrid approach is presented to manage the state explosion problem in model checking of systems specified by GTS for reachability verification and safety refutation by detecting deadlock as well. The suggested approach searches the state space intelligently, using a fuzzy genetic algorithm to find the state in which the specified property is verified or refuted. Moreover, this work evaluates the suggested solution by checking toolset of GROOVE, and some modification is done in the source code by Java language. In this work, the methods based on GA, PSO, and PSO-GSA algorithms that presented for deadlock detection, used for verifying the reachability property by changing their fitness function. These new-implemented methods are applied to evaluate the efficiency of the proposed approach for reachability verification. The results of applying the proposed algorithm on several well-known case studies reveal that the FGA approach could generally improve the speed of the deadlock detection and reachability verification in comparison with previous methods. Also, the length of the counterexamples indicates a more significant decrease than the algorithms based on GA, PSO, and PSO-GSA. However, it should be noted that the suggested method, like other proposed meta-heuristic approaches, is not a correct solution. If these solutions could not detect the deadlock or find a specified reachability property, they could not claim that the given model does not contain the deadlock or reachable specified state. In future research, the efficiency of the suggested algorithm can be improved by using an enhanced fuzzy system. The meta-heuristic approaches, proposed to detect deadlocks, could be updated to verify the reachability, using the suggested fitness function in this paper. Applying a new fitness function for the proposed approach can improve the experimental results. ACRONYMS Fuzzy Logic Controllers FLC Fuzzy systems FS Genetic algorithm GA Graph transformations system GTS Gravitational search algorithm GSA Negative application condition NAC Particle swarm optimization PSO State spaceexplosion SSE ACKNOWLEDGMENT We acknowledge the financial support of this work by the Hungarian-Mexican bilateral Scientific and Technological (2019-2.1.11-TÉT-2019-00007) project. The research presented in this paper was carried out as part of the EFOP- 3.6.2-16-2017-00016 project in the framework of the New Szechenyi Plan. The completion of this project is funded by the European Union and co-financed by the European Social Fund. REFERENCES 1 C. Baier, J.P. Katoen, and K.G. Larsen, Principles of Model Checking, Vol. 2620264, Cambridge: MIT press, 2008. 2 L. Baresi and R. Heckel, Tutorial introduction to graph transformation: A software engineering perspective, Graph Transformation (ICGT) 2002. 3 R. Yousefian and V. Rafe, and M. Rahmani, A heuristic solution for model checking graph transformation systems, Appl. Soft. Comput. 24 (2014) 169-180. 4 M. Moradi, V. Rafe, R. Yousefian, and A. Nikanjam, A Meta-Heuristic Solution for Automated Refutation of Complex Software Systems Specified through Graph Transformations, Appl. Soft. Comput. 33 (2015) 136-149. 5 R. Yousefian, S. Aboutorabi, and V. Rafe, A greedy algorithm versus metaheuristic solutions to deadlock detection in Graph Transformation Systems, J. Intell. Fuzzy Syst. 31(1) (2016) 137–149. 6 E. Pira, V. Rafe, and A. Nikanjam, EMCDM: Efficient model checking by data mining for verification of complex software systems specified through architectural styles, Appl. Soft. Comput. 49 (2016)1185-1201. 7 E. Pira, V. Rafe, and A. Nikanjam, Deadlock detection in complex software systems specified through graph transformation using Bayesian optimization algorithm, J. Syst. Software 131 (2017) 181- 200. 8 R. Heckel, Graph Transformation in a Nutshell, Electronic Notes in Theoretical Computer Science (ENTCS) 148(1) (2006) 187-198. 9 L.A. Zadeh, Fuzzy algorithms, Inf. and Control 12(2) (1968) 94-102. 10 F. Herrera, m. Lozano, Fuzzy adaptive genetic algorithms: design, taxonomy, and future directions, Soft Comput. 7(8) (2003) 545-562. 11 I. Nedeljkovic, Image classifcation based on fuzzy logic, The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences 34(30) (2004) 3–7. 12 S.M. Odeh, A.M. Mora, M.N. Moreno, and J.J. Merelo, A Hybrid Fuzzy Genetic Algorithm for an Adaptive Traffic Signal System, Advances in Fuzzy Syst. 2015. 13 S.N. Sivanandam and S.N. Deepa, Introduction to Genetic Algorithms, Springer, 2008. 14 Q. Li, Y. Yin, Z. Wang, and G. Liu, Comparative Studies of Fuzzy Genetic Algorithms, Advances in Neural Netw. 4499 (2007) 251-256. 15 V. Rafe, A.T. Rahmani, L. Baresi and P. Spoletini, Towards automated verification of layered graph transformation specifications, IET Softw. 3 (2009) 276–291. 16 G.Francesca, A.Santone, G.Vaglini, M.L.Villani, Ant Colony Optimization for Deadlock Detection in Concurrent Systems, 35th IEEE Annual Computer Softw. and Applications Conference (2011) 108-117. 17 E. Alba and F. Chicano, Ant ColonyOptimization in Model Checking, 11th international conference on Computer Aided Syst. Theory, Spain (2007) 523-530. 18 L.M. Duarte, L. Foss, R. Wagner, and T. Heimfarth, Model Checking the Ant Colony Optimisation, Distributed, Parallel and Biologically Inspired Systems, IFIP Advances in Information and Communication Technology 329 (2010) 221-232. 19 E. Alba and J.M. Troya, Genetic Algorithms for Protocol Validation, International Conference on Parallel Problem Solving from Nature PPSN IV, Springer, Berlin, Heidelberg (1996) 869-879. 20 A. Vardhan, Learning to Verify Systems, University of Illinois at Urbana-Champaign, 2006. 21 G.Francesca, A.Santone, G.Vaglini, M.L.Villani, Ant Colony Optimization for Deadlock Detection in Concurrent Systems, 35th IEEE Annual Computer Software and Applications Conference (2011) 108-117.
• 13.
  22 E. Albaand F. Chicano, ACOhg: Dealing with Huge Graphs, Proceedings of the 9th annual conference on Genetic and evolutionary computation, ACM (2007) 10-17. 23 E. Alba and F. Chicano, Searching for Liveness Property Violations in Concurrent Systems with ACO, 10th Annual Conference on Genetic and Evolutionary Computation, USA: ACM, Atlanta, Georgia, 2008. 24 H.C.W. Lau, D. Nakandala, and L. Zhao, Development of a Hybrid Fuzzy Genetic Algorithm Model for Solving Transportation Scheduling Problem, J. of Inf. Syst. and Technology Management 12(3) (2015) 505-524. 25 A. Schmidt, Model Checking of Visual Modeling Languages, M.S.D. Thesis, Budapest University of Technology, Hungary, 2004. 26 D. Swaroop, String stability of interconnected systems: An application to platooning in automated highway systems, California Partners for Advanced Transit and Highways (PATH), 1997. 27 J.H. Hausmann, Dynamic Meta Modeling: A Semantics Description Technique for Visual Modeling Techniques, Ph.D. Thesis, Universität Paderborn, Germany, 2005. 28 J. Gaschnig, Performance measurement and analysis of certain search algorithms, Ph.D. Thesis, Carnegie Mellon University Pittsburgh, PA, USA, 1979.