Introduction to the computing theory in automata

1 Introduction to Automata Theory Reading: Chapter 1

2 What is Automata Theory?  Study of abstract computing devices, or “machines”  Automaton = an abstract computing device  Note: A “device” need not even be a physical hardware!  A fundamental question in computer science:  Find out what different models of machines can do and cannot do  The theory of computation  Computability vs. Complexity

3 Alan Turing (1912-1954)  Father of Modern Computer Science  English mathematician  Studied abstract machines called Turing machines even before computers existed  Heard of the Turing test? (A pioneer of automata theory)

4 Theory of Computation: A Historical Perspective 1930s • Alan Turing studies Turing machines • Decidability • Halting problem 1940-1950s • “Finite automata” machines studied • Noam Chomsky proposes the “Chomsky Hierarchy” for formal languages 1969 Cook introduces “intractable” problems or “NP-Hard” problems 1970- Modern computer science: compilers, computational & complexity theory evolve

5 Languages & Grammars Or “words” Image source: Nowak et al. Nature, vol 417, 2002  Languages: “A language is a collection of sentences of finite length all constructed from a finite alphabet of symbols”  Grammars: “A grammar can be regarded as a device that enumerates the sentences of a language” - nothing more, nothing less  N. Chomsky, Information and Control, Vol 2, 1959

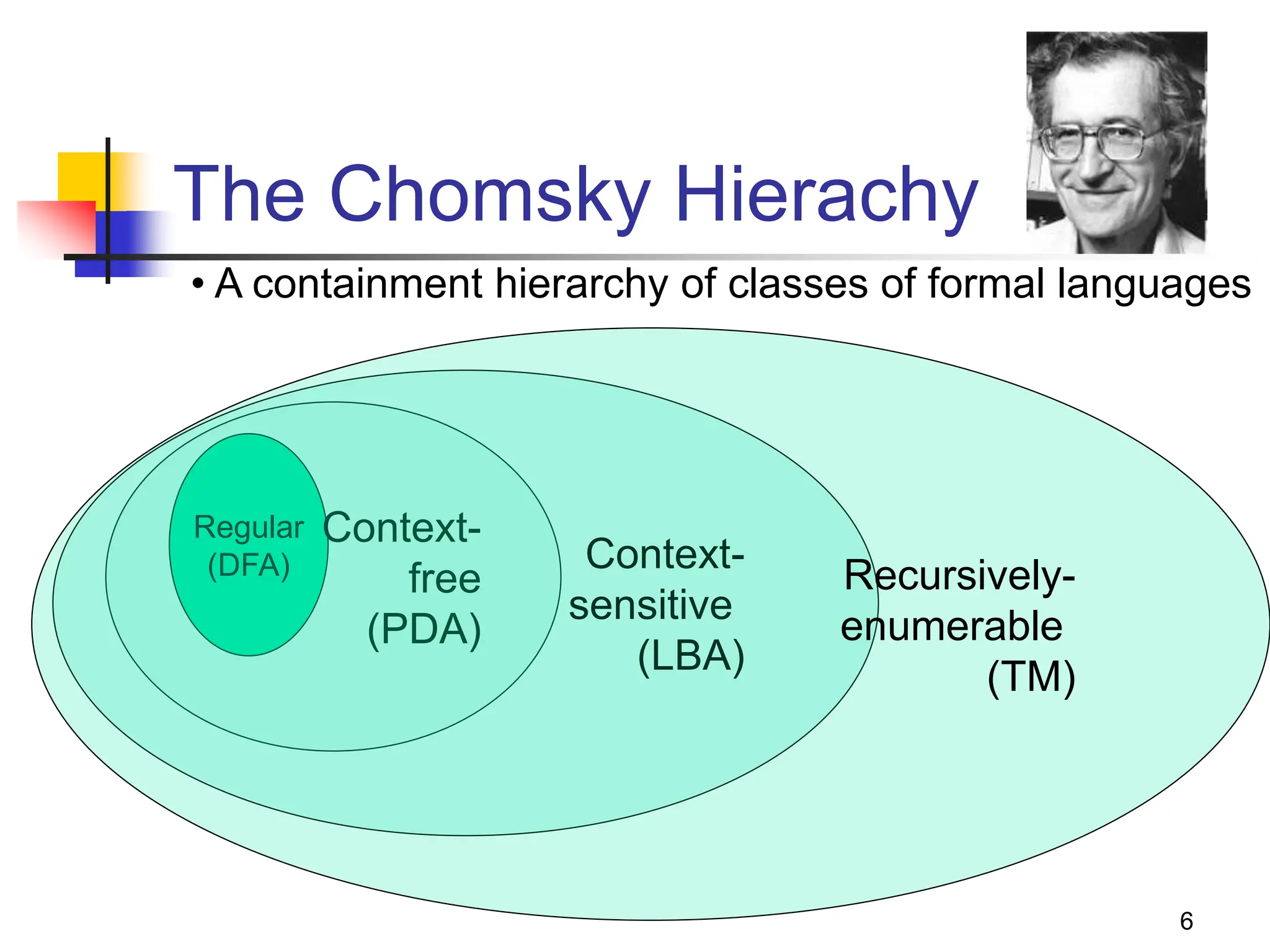
6 The Chomsky Hierachy Regular (DFA) Context- free (PDA) Context- sensitive (LBA) Recursively- enumerable (TM) • A containment hierarchy of classes of formal languages

7 The Central Concepts of Automata Theory

8 Alphabet An alphabet is a finite, non-empty set of symbols  We use the symbol ∑ (sigma) to denote an alphabet  Examples:  Binary: ∑ = {0,1}  All lower case letters: ∑ = {a,b,c,..z}  Alphanumeric: ∑ = {a-z, A-Z, 0-9}  DNA molecule letters: ∑ = {a,c,g,t}  …

9 Strings A string or word is a finite sequence of symbols chosen from ∑  Empty string is  (or “epsilon”)  Length of a string w, denoted by “|w|”, is equal to the number of (non- ) characters in the string  E.g., x = 010100 |x| = 6  x = 01  0  1  00  |x| = ?  xy = concatentation of two strings x and y

10 Powers of an alphabet Let ∑ be an alphabet.  ∑k = the set of all strings of length k  ∑* = ∑0 U ∑1 U ∑2 U …  ∑+ = ∑1 U ∑2 U ∑3 U …

11 Languages L is a said to be a language over alphabet ∑, only if L  ∑*  this is because ∑* is the set of all strings (of all possible length including 0) over the given alphabet ∑ Examples: 1. Let L be the language of all strings consisting of n 0’s followed by n 1’s: L = {,01,0011,000111,…} 2. Let L be the language of all strings of with equal number of 0’s and 1’s: L = {,01,10,0011,1100,0101,1010,1001,…} Definition: Ø denotes the Empty language  Let L = {}; Is L=Ø? NO

12 The Membership Problem Given a string w ∑*and a language L over ∑, decide whether or not w L. Example: Let w = 100011 Q) Is w  the language of strings with equal number of 0s and 1s?

13 Finite Automata  Some Applications  Software for designing and checking the behavior of digital circuits  Lexical analyzer of a typical compiler  Software for scanning large bodies of text (e.g., web pages) for pattern finding  Software for verifying systems of all types that have a finite number of states (e.g., stock market transaction, communication/network protocol)

14 Finite Automata : Examples  On/Off switch  Modeling recognition of the word “then” Start state Final state Transition Intermediate state action state

15 Structural expressions  Grammars  Regular expressions  E.g., unix style to capture city names such as “Palo Alto CA”:  [A-Z][a-z]*([ ][A-Z][a-z]*)*[ ][A-Z][A-Z] Start with a letter A string of other letters (possibly empty) Other space delimited words (part of city name) Should end w/ 2-letter state code

17 Deductive Proofs From the given statement(s) to a conclusion statement (what we want to prove)  Logical progression by direct implications Example for parsing a statement:  “If y≥4, then 2y≥y2.” (there are other ways of writing this). given conclusion

18 Example: Deductive proof Let Claim 1: If y≥4, then 2y≥y2. Let x be any number which is obtained by adding the squares of 4 positive integers. Given x and assuming that Claim 1 is true, prove that 2x≥x2  Proof: 1) Given: x = a2 + b2 + c2 + d2 2) Given: a≥1, b≥1, c≥1, d≥1 3)  a2≥1, b2≥1, c2≥1, d2≥1 (by 2) 4)  x ≥ 4 (by 1 & 3) 5)  2x ≥ x2 (by 4 and Claim 1) “implies” or “follows”

19 Quantifiers “For all” or “For every”  Universal proofs  Notation*=? “There exists”  Used in existential proofs  Notation*=? Implication is denoted by =>  E.g., “IF A THEN B” can also be written as “A=>B” *I wasn’t able to locate the symbol for these notation in powerpoint. Sorry! Please follow the standard notation for these quantifiers.

20 Proving techniques  By contradiction  Start with the statement contradictory to the given statement  E.g., To prove (A => B), we start with:  (A and ~B)  … and then show that could never happen What if you want to prove that “(A and B => C or D)”?  By induction  (3 steps) Basis, inductive hypothesis, inductive step  By contrapositive statement  If A then B ≡ If ~B then ~A

21 Proving techniques…  By counter-example  Show an example that disproves the claim  Note: There is no such thing called a “proof by example”!  So when asked to prove a claim, an example that satisfied that claim is not a proof

22 Different ways of saying the same thing  “If H then C”: i. H implies C ii. H => C iii. C if H iv. H only if C v. Whenever H holds, C follows

23 “If-and-Only-If” statements  “A if and only if B” (A <==> B)  (if part) if B then A ( <= )  (only if part) A only if B ( => ) (same as “if A then B”)  “If and only if” is abbreviated as “iff”  i.e., “A iff B”  Example:  Theorem: Let x be a real number. Then floor of x = ceiling of x if and only if x is an integer.  Proofs for iff have two parts  One for the “if part” & another for the “only if part”

24 Summary  Automata theory & a historical perspective  Chomsky hierarchy  Finite automata  Alphabets, strings/words/sentences, languages  Membership problem  Proofs:  Deductive, induction, contrapositive, contradiction, counterexample  If and only if  Read chapter 1 for more examples and exercises  Gradiance homework 1

Introduction to the computing theory in automata

More Related Content

Similar to Introduction to the computing theory in automata

More from AbubakarSadiq69

Recently uploaded

Introduction to the computing theory in automata

Editor's Notes