Download to read offline
Recursion is used in programming languages to use a procedure multiple times when we needed
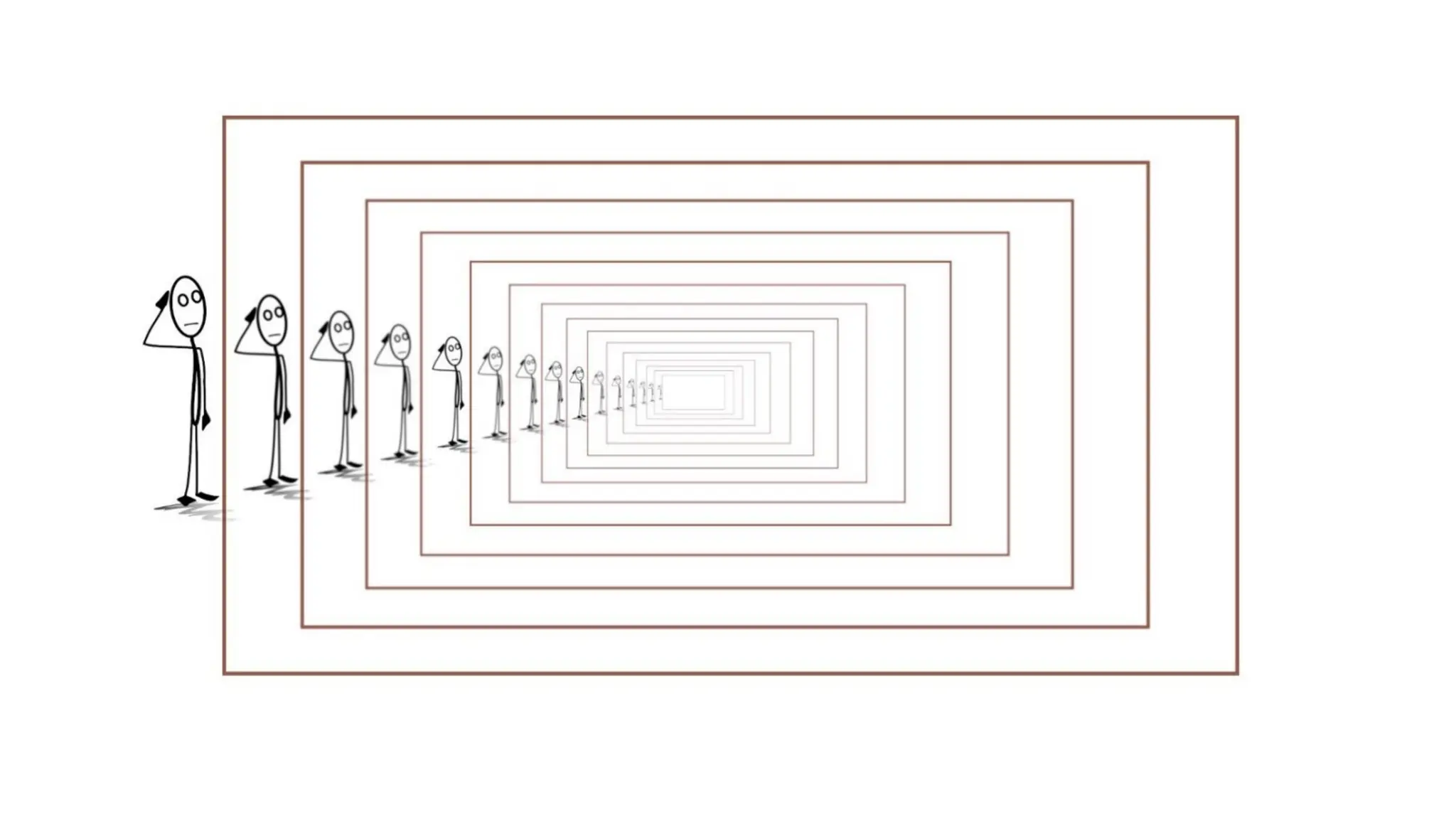
- 2. Recursion is aprogramming technique where a function calls itself directly or indirectly to solve smaller instances of a problem until it reaches a base case. This approach breaks down complex problems into simpler sub-problems, making them easier to solve.
- 3. Recursion is particularlyuseful in traversing hierarchical data structures like trees and graphs, where each node can be viewed as a smaller instance of the same problem.
- 4. Working of Recursion: •Recursionperforms a number of repetitive calls to the function from within the function. The recursive condition performs the repeating calls to the function until the base case is met. The base case is present inside the function, and once the condition of the base case is satisfied, it stops the execution.
- 5.
- 6. In the factorialfunction, we have to perform many repetitive calls to the function. In this example, the recursive condition would be n*factorial(n-1); factorial is the function's name, and the value of n is 5
- 8. First, in thisfunction, 5 will be multiplied with factorial(5-1), then 4 is passed to the function. Similarly, in the next iteration, 4 is multiplied with factorial(4-1). This will continue till the value of n becomes 1. Please note that the direction of execution can be - Top to down cout<<n; function(n-1);
- 9. Here, printing ofcode is done before the recursive call. Bottom to up function(n-1); cout<<n; Here, printing is done after the recursive call.
- 10. Types of Recursion: •Tail Recursion: The recursive call is the last statement in the function • Head Recursion: The recursive call is made before processing the current function’s operations. • Tree Recursion: A function calls itself multiple times, creating a tree-like call structure. • Nested Recursion: A recursive function is passed as an argument to itself.
- 11. A recursive functionconsists of: • Base case: The condition where the recursion stops. Without this, the function would call itself indefinitely. • Recursive case: The part where the function calls itself with a modified parameter to approach the base case.
- 12. Reasons for usingRecursion • Simplifies complex problems • Elegant code • Divide and conquer • Mathematical problems • Handles dynamic structures • Algorithm Design • Simplifies backtracking
- 13. Simplifies complex problems: Certainproblems, like tree traversal, are naturally recursive. Breaking the problem into smaller sub problems mirrors the problem structure. Examples: Traversing a binary tree, or calculating Fibonacci numbers.
- 14. Elegant code: Recursive functionsoften lead to more concise and readable code compared to their iterative counterparts. Example: Writing a factorial function is more natural with recursion than with loops.
- 15. Divide and Conquer: Recursionis a foundation stone of the divide- and-conquer strategy, where problems are divided into sub problems, solved recursively, and then combined. Example: Merge Sort, Quick Sort.
- 16. Mathematical problems: Many mathematicalproblems like combinatorics and sequence generation naturally fit a recursive approach. Example:
- 17. Handles Dynamic Structures: Recursivetechniques are particularly useful for processing dynamic data structures like trees and graphs. Example: Depth-First Search (DFS) for graphs.
- 18. Algorithm Design: Recursive thinkinghelps design efficient algorithms for problems like searching, sorting and backtracking. Example: N-Queens problem, Sudoku solver.
- 19. Simplifies backtracking: Recursion iscommonly used in backtracking algorithms to explore all possible configurations and return results upon finding a valid solution. Example: Maze solving, finding permutations.
- 20.
- 21. The call stackis a fundamental concept in programming, particularly in recursion. It is a stack data structure used by the system to manage function calls and their execution.
- 22.
- 23. Function call: When afunction is called, its execution context (parameters, local variables, and return address) is stored as a "frame" on top of the call stack.
- 24. Pushing Frames: In recursion,each time a function calls itself, a new frame is pushed onto the stack to handle the new instance of the function.
- 25. Base Case: The recursioncontinues until the base case is reached. At this point, no further recursive calls are made, and the function begins returning values.
- 26. Stack Unwinding (PoppingFrames): (After the base case is reached, the stack starts unwinding): • The most recent frame (representing the latest function call) is popped off the stack. • The return value from this function is passed to the previous frame on the stack. • This process continues until the stack is empty and the initial call completes.